Импеданс - полное электрическое сопротивление цепи переменному току.

Абсолютная величина (модуль) электрического импеданса определяется выражением

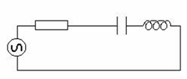
Полная цепь переменного тока - это цепь из генератора, а также R, C, и L

элементов, взятых в разных сочетаниях и количествах.

Для разбора проходящих в электрических цепях процессов используют полные

последовательные и параллельные цепи.

Последовательная цепь - это такая цепь, где все элементы могут быть

соединены последовательно, один за другим.

В параллельной цепи R, C, L элементы соединены параллельно.

Особенности полной цепи:

1.Соблюдается закон Ома

2.Полная цепь оказывает переменному току сопротивление. Это сопротивление

называется полным (мнимым, кажущимся) или импедансом.

3.Импеданс зависит от сопротивления всех элементов цепи, обозначается Z и

вычисляется не простым, а геометрическим (векторным) суммированием. Для

последовательно соединенных элементов формула импеданса имеет следующее

значение:

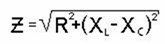
здесь:

Z - импеданс последовательной цепи,

R - активное сопротивление,

XL – индуктивное и XC – ёмкостное сопротивление,

L - индуктивность катушки (генри),

C - ёмкость конденсатора (фарад).

импеданс изменяется с изменением частоты

тока, на котором проводится измерение: при увеличении частоты реактивная составляющая импеданса уменьшается. Зависимость импеданса от частоты тока называется дисперсией импеданса.

Изменение импеданса с частотой обусловлено также зависимостью поляризации от периода Т переменного тока. Если время, в течение которого

электрическое поле направлено в одну сторону (Т/2), больше времени релаксации τ какого-либо вида поляризации, то поляризация достигает своего наибольшего значения, и до тех пор, пока T/2>τ, эффективная диэлектрическая проницаемость и проводимость объекта не будут изменяться с частотой. Если же при увеличении частоты полупериод T/2 переменного тока становится меньше времени релаксации, то поляризация не успевает достигнуть своего максимального значения. После этого диэлектрическая проницаемость начинает

уменьшаться с частотой, а проводимость - возрастать.

Электрический диполь.

Поле диполя

Электрический диполь - это система из двух одинаковых по модулю точечных электрических зарядов, расположенных на некотором расстоянии друг от друга(плечо диполя).

основная характеристика диполя-его электрический(дипольный)момент- вектор, равный произведению заряда на плечо диполя, направленный от отрицательного заряда к положительному.

p = dl.

Единицей электрического момента диполя является кулон-метр.

На диполь в однородном электрическом поле действует вращающий момент, зависящий от электрического момента, ориентации диполя в поле и напряженности поля. На диполь действует сила, зависящая от его электрического момента и степени неоднородности поля

Если диполь ориентирован в неоднородном электрическом поле не вдоль силовой линии, то на него дополнительно действует еще и вращающий момент. Свободный диполь практически всегда втягивается в область больших значений напряженности поля.

сам диполь является источником тока.

Понятие о мультиполе.

Диполь является частным случаем системы электрических зарядов, обладающих определенной симметрией. Общее название подобных распределений зарядов – электрические мультиполя (I = 0, 1, 2 и т. д.), число зарядов мультиполя определяется выражением 21.

Так, мультиполем нулевого порядка (20 = 1) является одиночный точечный заряд, мультиполем первого порядка (21 = 2) – диполь, мультиполем второго порядка (22 = 4) – квадруполь, мультиполем третьего порядка (23 = 8) – октуполь и т. д. Потенциал поля мультиполя убывает на значительных расстояниях от него (R > d, где d – размеры мультиполя)

пропорционально I/R1+1. Если заряд распределен в некоторой области пространства, то потенциал электрического поля вне системы зарядов можно представить в виде некоторого приближенного ряда:

Здесь R – расстояние от системы зарядов до точки А с потенциалом Ф;

f1, f2, f3…. – некоторые функции, зависящие от вида мультиполя, его заряда и от направления на точку А.

Первое слагаемое соответствует монополю, второе – диполю, третье – квадруполю и т. д. В случае нейтральной системы зарядов первое слагаемое равно нулю.