Добавочное давление под изогнутой поверхностью жидкости. Формула Лапласа.

Если поверхность жидкости по каким-либо причинам искривлена, то силы поверхностного натяжения, действующие на молекулы поверхностного слоя направлены под углом и уже не компенсируют друг друга, а их результирующая направлена к центру кривизны поверхности и оказывает на поверхность дополнительное молекулярное давление Δр, величина которого рассчитывается по формуле Лапласа, которая для сферической поверхности радиуса R принимает вид:

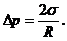(3)

Поскольку силы, создающие дополнительное молекулярное давление, направлены всегда к центру кривизны поверхности, то и дополнительному давлению Δр приписывают такую же направленность. В результате молекулярное давление под выпуклой поверхностью жидкости всегда больше, а под вогнутой – меньше, чем давление p₀ под плоской поверхностью:

р_вып=р₀ + Δр;

р_вогн=р₀ – Δр; (4)

Явление смачивания.

При контакте жидкости с твердым телом вследствие межмолекулярных взаимодействий возникают явления смачивания или не смачивания. Если силы притяжения между молекулами жидкости и твердого тела больше сил притяжения между молекулами жидкости: F_ж-тв > F_ж-ж, то жидкость будет растекаться по поверхности твердого тела, это явление и называют смачиванием. Если же силы притяжения между молекулами жидкости и твердого тела меньше сил притяжения между молекулами жидкости: Fж-тв < Fж-ж., то жидкость будет стремиться уменьшить свою поверхность, собираясь в каплю (рис.4). Такое явление называют несмачиванием. Одна и та же жидкость может быть смачивающей для одного твердого тела и не смачивающей для другого.

Поверхности, смачиваемые водой, называют гидрофильными, а не смачиваемые ею – гидрофобными.

Количественной мерой смачивания служит краевой угол θ, образуемый поверхностью твердого тела и касательной, проведенной к поверхности жидкости в точке их соприкосновения, причем жидкость находится внутри этого угла (см. рис.4). При смачивании 0≤ θ< 90^o и чем меньше угол θ, тем сильнее смачивание. Если θ=0, то смачивание называют полным или идеальным. При идеальном смачивании капля жидкости растекается по поверхности твердого тела, пока не покроет всю поверхность или пока не образуется мономолекуляр­ный слой.

При несмачивании 90^o < θ≤ 180^o и чем больше угол θ,чем сильнее выражено несмачивание, при θ=180^о будет полное несмачивание. В этом случае жидкость не прилипает к поверхности твердого тела и легко скатывается с нее.

Капиллярные явления.

Явления изменения высоты уровня жидкости в капиллярах по сравнению с уровнем жидко­сти в широком сосуде называются капиллярными явлениями(Рис.5). Если жидкость смачивает стенки капилляра, то образуется вогнутый мениск радиуса r, молекулярное давление под которым на Δр меньше, чем под плоской поверхностью в широком сосуде, сообщающимся с капилляром, вследствие чего жидкость в капилляре выталкивается вверх до тех пор, пока весовое давление образовавшегося столба жидкости высотой h не скомпенсирует добавочное молекулярное давление Δр:

Δр = ρgh, (5)

где ρ – плотность жидкости, g – ускорение свободного падения.

Если жидкость не смачивает капилляр, то образуется выпуклый мениск, молекулярное давление под которым вытесняет жидкость ниже исходного уровня на глубину h, удовлетворяющую условию (5).

Таким образом, в капилляре жидкость поднимается (или опускается) на такую высоту h, при которой гидростатическое давление столба жидкости уравновешивает избыточное молекулярное давление, обусловленное кривизной мениска:

. (6)

Если радиус кривизны мениска равен R, то, подставляя (5.3а) в (5.6), получим:

. (7)

Здесь учтена связь между радиусом капилляра r и радиусом кривизны мениска R = r/cosθ,гдеθ – краевой угол.

Из формулы (5.7) видно, что чем тоньше капилляр (r) и лучше смачивание (меньше θи, соответственно, большеcosθ), тем выше поднимается жидкость по капилляру. При идеальном смачивании (θ=0, cosθ=1, R=r) высота подъема максимальна:

(7а)

Смачивающая жидкость хорошо проникает в мелкие поры тела и удерживается в них. Благодаря этому явлению пористые вещества могут удерживать значительное количество жидкости даже из паров воздуха, что приводит к увлажнению белья, ваты в сырых помещени­ях, затрудняет сушку гигроскопических тел.

Капиллярные явления весьма распространены, ими в частности, обусловлено поднятие воды в почве, по корневой системе растений, движение биологических жидкостей по системе мелких сосудов и канальцев и многие другие явления.

Несмачивающая жидкость «выталкивается» из капилляра и не может глубоко проникнуть в капилляры и поры твердого тела.

Определение коэффициента поверхностного натяжения жидкости методом Ребиндера(метод определения максимального давления в пузырьке).

Исследуемая жидкость помещается в пробирку 1 (см. рис.6), в которую затем вертикально опускается капиллярная трубка 2, проходящая сквозь пробку, плотно закрывающую пробирку. Узкий конец капиллярной трубки касается мениска исследуемой жидкости (или заглублен в нее не более, чем на 0,5мм), а другой сообщается с атмосферой.

В стеклянном сосуде 3 с краном 4 находится вода. Сосуд закрыт плотно пригнанной пробкой, причём давление над поверхностью воды p₁ такое же, как над поверхностью исследуемой жидкости и в левом плече U –образного манометра 5.

При открытом кране 4 из сосуда 3 начинает вытекать вода. Объём воды в сосуде 3 уменьшается, а значит, объём воздуха над водой в сосуде увеличивается. Температура воздуха остаётся неизменной, масса воздуха тоже не меняется, из чего следует, что выполняется закон Бойля и Мариотта: для газа одинаковой массы при постоянной температуре произведение давления на объём постоянной, т.е. pV=const или p₁V₁=р₂V₂. При увеличении объёма воздуха над водой в сосуде 3 давление p₁ понижается, а значит, оно понизится и над исследуемой жидкостью, и в левом столбике манометра.

При некотором давлении р₁ над поверхностью исследуемой жидкости из конца капиллярной трубки 2 под действием разности атмосферного давления р_атм и давления р₁ выдавливается в жидкость воздушный пузырёк. Эта разность давлений Δр= р_атм – p₁ измеряется манометром и равна ρgh, где ρ - плотность жидкости, залитой в манометр, h - разность уровней этой жидкости в левом и правом столбике U-образной трубки манометра.

Давление, обусловленное силами поверхностного натяжения и стремящееся «схлопнуть» пузырек, определяется формулой Лапласа (3).

В момент отрыва пузырька эти давления равны и для эталонной и жидкости, коэффициент поверхностного натяжения σ₀ которой известен, можем записать:

, (8)

Аналогичную формулу можем записать и для исследуемой жидкости:

. (9)

Здесь h₀ и h₁– максимальная разность уровней жидкости в левом и правом коленах U-образного манометра в момент отрыва пузырька в пробирке с эталонной и исследуемой жидкостью соответственно.

Разделив уравнение (9) на (8), получим: . Отсюда получим формулу для определения поверхностного натяжения исследуемой жидкости:

. (10)

Порядок выполнения работы:

1. Налить достаточно (порядка 2/3 объёма) воды в сосуд 3 при закрытом кране 4 и плотно закрыть сосуд пробкой.

2. Налить в пробирку 1 одну из жидкостей (эталонную или исследуемую) так, чтобы опускаемая в пробирку капиллярная трубка 2, проходящая сквозь плотно закрытую пробку, своим узким концом была опущена ниже поверхности (мениска) исследуемой жидкости не более чем на 0,5-1,0 мм.

3. Открыть кран 4 сосуда 3, чтобы вода медленно вытекала каплями или очень тонкой струйкой. При этом разность уровней жидкости в левом и правом коленах U-образной трубки манометра будет увеличиваться, показывая разность давлений, которая стремится выдуть из капилляра пузырек воздуха.

4. В момент отрыва пузырька разность уровней h жидкости в левом и правом столбике U-образной трубки манометра будет максимальна. Ее следует зафиксировать и записать в табл. 1 для соответствующей жидкости.

5. Повторить определение h для каждой из исследуемых жидкостей по три раза и занести измерения в таблицу. Следить за тем, чтобы воды в сосуде 3 было достаточно (не менее 1/3 объема), и подливать ее по мере вытекания, не забывая плотно закрывать затем сосуд пробкой (иначе пузырьки выделяться не будут).

Таблица.1. Результаты измерений.

№ опыта	Эталонная жидкость	Исследуемые жидкости
h0, мм, вода	h1, мм розовый раствор	h2, мм голубой раствор
Среднее значениеσ, мН/м

6. Найти средние арифметические h_сред разности высот для каждой из жидкостей.

7. Рассчитать коэффициенты поверхностного натяжения розовой и голубой жидкости (соответственно σ_роз и σ_гол) по формуле (10) и занести их в таблицу.

8. Сравнить полученные значения σ_роз и σ_гол с коэффициентами поверхностного натяжения воды и спирта (σ_спирта = 22 мН/м = 22 · 10^–3 Н/м при +20 ºС) и сделать вывод о том, какой из спиртовых растворов (розовый или голубой) больше разбавлен водой.

9. Рассчитать случайную ошибку косвенного измерения для обоих цветных растворов, пользуясь знаниями, полученными из раздела «Теория ошибок».

Контрольные вопросы:

1. Чем обусловлено возникновение потенциальной энергии поверхностного слоя жидкости? От чего зависит эта энергия?

2. Каков физический смысл коэффициента поверхностного натяжения, от чего он зависит, какова его размерность?

3. Чему равны и как направлены силы поверхностного натяжения? Каким образом проявляются эти силы и как их можно измерить?

4. Чем вызвано молекулярное давление поверхностного слоя на жидкость?

5. Каково добавочное давление под изогнутой поверхностью жидкости? Как его рассчитать?

6. Чем обусловлены явления смачивания и не смачивания? Что такое краевой угол, от чего зависит его величина?

7. Чем обусловлены капиллярные явления и как они проявляются? Как рассчитать высоту подъема (опускания) жидкости в капиллярных трубках?

8. В чем сущность газовой эмболии и каковы условия ее возникновения?

9. Какова роль поверхностного натяжения альвеолярного сурфактанта легких в процессе дыхания?

10. Опишите метод Ребиндера и получите расчётную формулу для определения коэффициента поверхностного натяжения этим методом.

11.Охарактеризуйте другие известные Вам методы определения коэффициента поверхностного натяжения жидкостей.

Решить задачи:

1. Добавочное давление Лапласа, обусловленное поверхностным натяжением воды при 20⁰С равно 96,9 кПа. Найти диаметр сферической капли тумана если σ₂₀=72,7 мН/м.

2. При определении коэффициента поверхностного натяжения методом отрыва капель было определено, что при температуре 10⁰С (σ₁₀=71,78 мН/м) перетяжка при отрыве капли дистиллированной воды имеет диаметр 6,1 мм. Определить массу капли.

3. Если в полностью смачиваемом капилляре диаметром 2,8 мм, погруженном в воду вертикально, вода поднялась на высоту 1 см, то коэффициент поверхностного натяжения воды будет равен … мН/м. (g = 9,8 м/с², плотность воды равна 10³ кг/м³).

Литература:

1. В.Г.Лещенко, Г.К.Ильич. Медицинская и биологическая физика.- Мн.: Новое знание. 2011.

2. А.Б.Крылов Поверхностное натяжение и связанные с ним явления.-Мн.:БГМУ 2008.

Лабораторная работа № 12. Определение вязкости
жидкости вискозиметром Оствальда.

Цель работы: Изучить законы течения вязкой жидкости. Научиться опред лять вязкость жидкости с помощью капиллярного вискозиметра Оствальда.

Теоретические основы.

Известно, что между молекулами реальной жидкости существуют сил взаимодействия. При течении жидкостиналичиеэтих сил проявляется каквнутреннее трение или вязкость жидкости и приводит к тому, что ее разные слои движутся с различными скоростями.

На рис.1 представлен случай, когда скорость верхнего слоя жидкости максимальна, а для нижнего - минимальна (например, течение воды в реке). Силы внутреннего трения направлены по каса­тельной к поверхности слоев.

Таким образом, в вязкой жидкости скорости движущихся слоев изменяются в направлении ОХ, перпендикулярном поверхности движущихся слоев жидкости. Количественно это изменение скорости движе­ния слоев жидкости характе­ризуется градиентом скорос­ти dv/dx, называемым также скоростью сдвига. Чем выше скорость сдвига, тем больше и сила трения между слоями движущейся жидкости. Сила F_тр внутреннего трения пропорциональна также площади соприкосновения S слоев жидкости, что отражено в формуле Ньютона для силы внутреннего трения:

F_тр = h S . (1)

Коэффициент h зависит от свойств жидкости и температуры и назы­вается коэффициентом внутреннего трения или вязкостью (динамичес­койвязкостью)жидкости.С ростом температуры вязкость жидкостей обычно уменьшается.

Единицей вязкости в Международной системе единиц является 1 Па·с (паскаль-секунда). Внесистемная единица вязкости – 1 пуаз (П) =0,1 Па·с.

Если вязкость жидкости h не зависит от градиен­та скорости, то такие жидкости называют ньютоновскими. К ним отно­сятся, как правило, однородные жидкости (вода, чистые растворители и др.). Если же вязкость зависит от гра­диента скорости, то жидкости называют неньютоновскими. Ими являются обычно неоднородные по составу жидкости, например, взвеси, суспензии и т.п. Типичнойненьютоновской жидкостьюявляетсякровь, так как она представля­ет собой взвесь форменных элементов (эритроцитов, лейкоцитов и др.) в плазме. Поэтому вязкость крови в различных участках сосудистой системы не одинакова из-за различных значений градиентов скорости, ре­ализующихся в движущейся крови.

Вязкость воды при температуре 20^оС составляет 1мПа×c или 1сП (сантипуаз), а средняя вязкость крови в норме - 4-5 мПа×с. При различных патологиях значения вязкости крови может изменяться от 1,7 до 22,9 мПа×с. Отношение вязкости крови к вязкости воды называют относи­тельной вязкостью крови.

На величину вязкости крови в жи­вом организме влияют температура, гематокрит, градиент скорости крови (подробнее см. [1]).

Течение жидкости характеризуется линиями тока. Это линии, ка­сательные к которым совпадают с направлением вектора скорости час­тиц жидкости в данной точке. Если линии тока жидкости непрерывны, то такое течение называется ламинарным, а если возникают завихрения, скорость частиц жидкости хаотически меняется, линии тока претерпевают разрывы, то движение жидкости называется турбулентным.

Характер течения жидкости - ламинарный или турбулентный - за­виситот плотности жидкости r, ее вязкости h, скорости течения v, диаметра трубы d, по которой течет жидкость. Существует безразмерный параметр, называемый числом Рейнольдса (Re), который позволяет определить характер течения:

Re = . (2)

Если число Рейнольдса не превышает некоторого критического значения Re_кр, то течение жидкости ламинарное. Если же Re > Re_кр , то течение становится тур­булентным. Для гладких цилиндрических труб Re_кр =2300. Для крови в разных участках сосудистого русла критическое число Рейнольдса может принимать значения 900÷1600.