Измерение связи между изучаемыми явлениями. Стандартизация относительных величин
¨ Измерение связи между изучаемыми явлениями.Целью проведения многих медико-биологических исследований является выявление и количественная оценка взаимосвязей между изучаемыми явлениями. В большинстве случаев это даёт возможность прогнозирования различных характеристик объекта исследования. Основанием для гипотезы о наличии связи между изучаемыми явлениями чаще всего служит одновременное и параллельное изменение их количественных характеристик в динамическом наблюдении.
По характеру все связи между явлениями делятся на два вида:
- функциональную связь по типу y = f(x), при которой любое изменение одной величины сопровождается строго заданным изменением другой величины: y = 2x; y = x2;
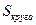= πr2; y = x2 + x и т.д.; - корреляционную (статистическую) связь, когда при изменении одной величины другая может принимать различные значения: изменение частоты пульса при повышении температуры тела на один градус у разных людей, увеличение массы тела в зависимости от роста человека, количество мутаций при увеличении дозы ионизирующего излучения, рост заболеваемости при увеличении загрязнения атмосферного воздуха и т.п.
В области медицины и биологии функциональные связи встречаются крайне редко. В подавляющем большинстве случаев взаимозависимости между изучаемыми явлениями являются корреляционными, которые оцениваются на основе расчётов коэффициентов корреляции. Необходимыми условиями для использования коэффициентов корреляции в практике работы являются:
ü для установления и количественной оценки корреляционной связи между изучаемыми явлениями необходимо иметь множественные наблюдения (в соответствии с законом больших чисел); изучение и оценка такой связи на основе единичных наблюдений даст ошибочный результат;
ü для расчётов коэффициентов корреляции следует использовать качественно однородные группировки признаков (аналогично методологическим требованиям к расчёту средних величин).
При расчёте коэффициентов корреляции определяются и оцениваются:
А) теснота связи между изучаемыми явлениями – величина коэффициента корреляции, определяющая насколько сильно колеблются значения полученных величин статистического наблюдения от средней величины; более тесной считается связь, когда с изменением одной величины вторая приобретает несколько разных, но близких друг к другу значений; если эти значения существенно разбросаны друг от друга и от средней величины, корреляционная связь между изучаемыми явлениями считается менее тесной; количественная оценка степени тесноты связи:
0,0 - отсутствие связи между изучаемыми явлениями;
0,1 – 0,29 - связь слабой степени тесноты;
0.3 – 0,69 - связь средней степени тесноты;
0,7 – 0.99 - связь сильной степени тесноты;
1,0 - связь полная (функциональная).
Б) направленность (форма) связи между изучаемыми явлениями: если величина полученного коэффициента корреляции имеет знак (+), то изучаемая связь является прямой (при увеличении величин одного признака увеличиваются значения второго признака); если величина рассчитанного коэффициента корреляции имеет знак (-), то такая связь между явлениями является обратной (при увеличении одного признака второй уменьшается).
Общая цель:
Освоить методику вычисления и анализа коэффициента корреляции по методу Пирсона и коэффициента ранговой корреляции Спирмена.
Конкретные цели:
| Знать: | Уметь: |
| 1. методику измерение и оценку связи между явлениями путем расчета коэффициента корреляции по методу Пирсона; 2. методику измерение и оценку связи между явлениями путем расчета коэффициента ранговой корреляции | 1. оценивать связь между явлениями путем расчета коэффициента корреляции. 2. оценивать связь между явлениями, сделать вывод |
Контрольные вопросы для определения исходного уровня знаний:
1. Что называется корреляционной связью?
2. Перечислите виды корреляционной связи.
3. Что называется функциональной связью?
4. Каковы принципы измерения связи между явлениями в стоматологии?
План практического занятия:
1. Контроль исходного уровня знаний.
2. Выполнение учебных задач: вычисление коэффициента корреляции по методу Пирсона и коэффициента ранговой корреляции;
3. Контроль практических навыков.
4. Выходной контроль уровня знаний.
Выполнение учебных задач по теме «Измерение связи между явлениями»:
Вариант №1
Задача 1. При изучении физического развития десятилетних мальчиков города А. были получены следующие данные:
| Рост (см) | Вес (кг) | ||
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции между ростом и весом (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | ||
Задача 2. При изучении распространенности парадонтита среди лиц разных возрастных групп, проживающих в городе А., были получены следующие данные:
| Возраст в годах | Распространенность парадонтита (в %) | ||
| 16 – 19 | 0,3 | ||
| 20 – 29 | 2,6 | ||
| 30 – 39 | 6,4 | ||
| 40 – 49 | 12,9 | ||
| 50 – 59 | 19,9 | ||
| 60 и старше | 17,8 | ||
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | ||
Вариант №2
Задача 1. При изучении физического развития мальчиков в возрасте 15 лет, проживающих в городе Б., были получены следующие данные:
| Рост (см) | Вес (кг) |
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции между ростом и весом (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. |
Задача 2. При изучении зависимости удельного веса лиц с санированной полостью рта от уровня образования в городе Б. были получены следующие данные:
| Образование | Число лиц с санированной полостью рта (%) | |||
| 8 классов | ||||
| 9 классов | ||||
| 10 классов | ||||
| Среднее специальное | ||||
| Незаконченное высшее | ||||
| Высшее | ||||
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | |||
Вариант №3
Задача 1. При изучении физического развития десятилетних мальчиков города К. были получены следующие данные:
| Рост (см) | Вес (кг) | ||
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции между ростом и весом (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | ||
Задача 2. При изучении зависимости пораженности зобом населения города К. от суточного содержания йода в воде и пище были получены следующие данные:
| Количество йода | Пораженность населения зобом | ||
| 0,2 | |||
| 0,6 | |||
| 1,1 | |||
| 0,8 | |||
| 2,5 | |||
| 4,4 | |||
| 10,9 | |||
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | ||
Вариант №4
Задача 1. При изучении физического развития десятилетних мальчиков города М. были получены следующие данные:
| Рост (см) | Вес (кг) | ||
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции между ростом и весом (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | ||
Задача 2. При изучении распространенности парадонтита среди лиц разных возрастных групп города М. были получены следующие данные:
| Возраст в годах | Распространенность парадонтита (в %) | |
| 15 – 19 | 0,5 | |
| 20 – 29 | 2,8 | |
| 30 – 39 | 6,6 | |
| 40 – 49 | 11,9 | |
| 50 – 59 | 18,9 | |
| 60 и старше | 16,8 | |
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | |
Вариант № 5
Задача 1. При изучении зависимости уровня гнойничковых заболеваний и травм у рабочих предприятия, полученные следующие данные:
| Годы | Число травм на 100 рабочих | Число гнойничковых заболеваний на 100 рабочих |
| 5,0 | 4,0 | |
| 6,1 | 3,5 | |
| 9,0 | 4,8 | |
| 8,6 | 5,5 | |
| 7,4 | 4,2 |
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции между числом травм и числом гнойничковых заболеваний (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками. |
Задача 2. По результатам выборочного исследования установлены следующие данные о числе госпитализированных больных с сердечно-сосудистой недостаточностью в связи с возрастом:
| Возраст в годах | Число больных с сердечно-сосудистой недостаточностью | ||
| до 20 | |||
| 20-29 | |||
| 30-39 | |||
| 40-49 | |||
| 50-59 | |||
| 60 и старше | |||
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | ||
Вариант №6
Задача 1. При изучении физического развития десятилетних мальчиков города М. были получены следующие данные:
| Рост (см) | Вес (кг) | ||
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции между ростом и весом (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | ||
Задача 2. При изучении распространенности парадонтита среди лиц разных возрастных групп города М. были получены следующие данные:
| Возраст в годах | Распространенность парадонтита (в %) | |
| 15 – 19 | 3,5 | |
| 20 – 29 | 5,8 | |
| 30 – 39 | 6,6 | |
| 40 – 49 | 11,9 | |
| 50 – 59 | 18,9 | |
| 60 и старше | 16,8 | |
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | |
Вариант №7
Задача 1. При изучении физического развития десятилетних мальчиков города М. были получены следующие данные:
| Рост (см) | Вес (кг) | ||
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции между ростом и весом (метод Пирсона). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | ||
Задача 2. При изучении распространенности кариеса среди лиц разных возрастных групп города М. были получены следующие данные:
| Возраст в годах | Распространенность кариеса (в %) | |
| 15 – 19 | ||
| 20 – 29 | ||
| 30 – 39 | ||
| 40 – 49 | ||
| 50 – 59 | ||
| 60 и старше | ||
| ТРЕБУЕТСЯ: | 1. Вычислить коэффициент корреляции рангов (метод Спирмена). 2. Определить ошибку коэффициента корреляции и его достоверности. 3. Дать оценку степени тесноты и характера связи между признаками развития. | |
Ориентировочная основа действий:
I . Алгоритм расчета коэффициента корреляции по методу квадратов (Пирсона):
1. Вычислите среднюю арифметическую простую для каждого вариационного ряда (Мx и Мy )
2. Найдите отклонении вариант от средней арифметической
dx = Vx - Мx
d y = V y – Мy
3. Вычислите произведение dx × d y
4. Определите ∑ dx × d y
5. Вычислите dx 2 и d y2
6. Найдите ∑ dx 2 и ∑ d y2
7. Вычислите произведение ∑ dx 2 × ∑ d y2
8. Рассчитайте коэффициент корреляции по методу квадратов (Пирсона) по формуле:
 |
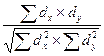II. Алгоритм расчета коэффициента ранговой корреляции (Спирмена):
1. Определите ранг вариант для каждого вариационного ряда
2. Вычислите разницу рангов (d)
3. Определите d 2
4. Найдите ∑ dx 2
5. Определите число сопряженных пар (n)
6. Рассчитайте коэффициент корреляции ранговой корреляции (Спирмена) по формуле:
 |
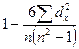III. Методика оценки коэффициента корреляции:
Оценка степени тесноты и характера связи:
| отсутствие связи | |
| до 0,29 | слабая |
| 0,3-0,69 | средняя |
| 0,7- 0,99 | сильная |
| 1,0 | полная |
| + | прямая |
| - | обратная |
Контрольные вопросы:
1. Что называется корреляционной связью?
2. Что называется функциональной связью?
3. Как различается по характеру корреляционная связь?
4. Формула для определения коэффициента корреляции (метод Пирсона).
5. Формула для определения коэффициента корреляции рангов (метод Спирмена).
6. Формула для определения ошибки коэффициента корреляции.
7. Какая величина определяет достоверность коэффициента корреляции?
8. Какие степени тесноты связи различают в зависимости от значения коэффициента корреляции?
Литература:
1. Социальная гигиена (медицина) и организация здравоохранения под редакцией академика РАМН Ю.П. Лисицына.- Казань, 1998.
2. Миняев В.А., Вишняков Н.И., Юрьев В.К. Социальная медицина и организация здравоохранения. Т.1. – С.-Петербург, 1998
3. Основы медицинской статистики. / Учебное пособие для студентов и выпускников стоматологического факультета для специальности 040400 – «Стоматология»:. В.Г. Дьяченко, В.Б. Пригорнев. ─ Хабаровск. Изд. Центр ГОУ ВПО ДВГМУ Росздрава. 2007. 174 с.
4. Белицкая Е. Я. Учебное пособие по медицинской статистике. «Медицина». Ленинградское отделение. 1972, с. 173.
5. Основы корреляционного анализа. Компьютерный образовательный курс «Основы биомедицинской статистики». Под ред. Н. А. Крючкова. Версия 1.0. Ставрополь-Москва; 2005.
6. Реброва О. Ю. Статистический анализ медицинских данных. М: МедиаСфе-ра2002. гл.12.
¨ Стандартизация относительных показателей
При сравнении и оценке относительных показателей существенное влияние на величину этих показателей может оказать неоднородность состава совокупностей, из которых рассчитаны показатели здоровья населения. Статистический метод, позволяющий исключить влияние различий, сравниваемых совокупностей неоднородных по своему составу, носит название метода стандартизации.
При применении метода стандартизации рассчитываются стандартизованные показатели, т. е. условные показатели, которые могли бы быть при условии одинакового состава совокупностей и которые могли бы исключить ошибки при анализе сравниваемых истинных относительных показателей. Существует три метода стандартизации - прямой, косвенный и обратный. Сравнивать с помощью метода стандартизации можно только сопоставимые явления.
Стандартизация – это метод сравнения показателей в качественно неоднородных совокупностях путем элиминирования (устранения) этой неоднородности. Стандарт – это величины, искусственно вводимые в условие решаемой задачи для элиминирования качественной неоднородности сравниваемых совокупностей.
Стандартизация позволяет решать три типа задач:
1. сравнивать показатели в качественно неоднородных группах (неоднородность может быть по диагнозам, полу, возрасту, социальному положению и т.д.);
2. получать вывод о влиянии какого-либо фактора на показатель: если после стандартизации по данному фактору результат изменился – влияние есть, если не изменился - нет;
3. устранять влияние какого-либо фактора на результат: если результативный показатель в какой-либо группе наблюдений в значительной мере обусловлен большими отличиями определенного фактора от обычных значений этого фактора, можно провести стандартизацию по данному фактору и проследить, как изменится результат.
Этапы стандартизации:
1. Вычисление обычных показателей.
2. Выбор стандарта.
3. Вычисление ожидаемых величин в соответствии со стандартом.
4. Определение стандартизованных показателей.
Сопоставление обычных и стандартизованных показателей
Общая цель:
Освоить методику применения метода стандартизации и расчета стандартизованных показателей прямым и косвенным методами.
Конкретные цели:
| Знать: | Уметь: |
| 1. Цель стандартизации относительных величин 2. Содержание этапов прямого метода стандартизации 3. Условия применения косвенного и обратного методов стандартизации | 1. Рассчитывать стандартные показатели прямым методом |
Контрольные вопросы для определения исходного уровня знаний:
1. В каких случаях применяется метод стандартизации?
2. Перечислите основные методы стандартизации относительных величин
3. Разъясните сущность прямого метода стандартизации
План практического занятия:
1. Контроль исходного уровня знаний.
2. Выполнение учебных задач: по вычислению показателей стандартизации прямым методом
3. Контроль практических навыков.
4. Выходной контроль уровня знаний.
Выполнение учебных задач по теме «Стандартизация относительных величин»:
Вариант №1
ЗадачаВычислить прямым методом стандартизованные показатели заболеваемости остеопорозом рабочих на двух предприятиях и сравнить их с показателями, вычисленными обычным путем. Сформулировать вывод.
| Стаж работы | Предприятие 1 | Предприятие 2 | ||
| Число рабочих | из них с остеопорозом | Число рабочих | из них с остеопорозом | |
| до 5 лет | ||||
| 6-10 лет | ||||
| 11-15 лет | ||||
| свыше 15 лет | ||||
| Всего |
Вариант №2
ЗадачаВычислить прямым методом стандартизованные показатели летальности в больнице №1 и №2 и сравнить их с показателями летальности, вычисленными обычным путем. Сформулировать вывод.
| Отделения | Больница №1 | Больница №2 | ||
| Число больных | Число умерших | Число больных | Число умерших | |
| Терапевтическое | ||||
| Хирургическое | ||||
| Инфекционное | ||||
| Всего |
Вариант №3
Задача Вычислить прямым методом стандартизованные показатели травматизма в двух цехах и сравнить их с показателями травматизма, вычисленными обычным путем. Сформулировать вывод.
| Профессия | Цех №1 | Цех №2 | ||
| Число рабочих | Число травм | Число рабочих | Число травм | |
| Токари | ||||
| Шлифовщики | ||||
| Слесари | ||||
| Прочие | ||||
| Всего |
Вариант №4
ЗадачаВычислить прямым методом стандартизованные показатели заболеваемости болезнями печени и желчных путей рабочих двух цехов и сравнить их с показателями заболеваемости, вычисленными обычным путем. Сформулировать вывод.
| Пол | Цех №1 | Цех №2 | ||
| Число рабочих | Число больных | Число рабочих | Число больных | |
| Мужчины | ||||
| Женщины | ||||
| Всего |
Вариант № 5
ЗадачаВычислить прямым методом стандартизованные показатели рождаемости в двух районах и сравнить их с показателями, вычисленными обычным путем. Сформулировать вывод.
| Возраст | Район А | Район Б | ||
| Число населения | Число родившихся | Число населения | Число родившихся | |
| До 19 лет | ||||
| 20 -29 лет | ||||
| 30 - 39 лет | ||||
| 40 и старше | ||||
| Всего |
Вариант №6
ЗадачаВычислить прямым методом стандартизованные показатели заболеваемости болезнями печени и желчных путей рабочих двух цехов и сравнить их с показателями заболеваемости, вычисленными обычным путем. Сформулировать вывод.
| Пол | Цех №1 | Цех №2 | ||
| Число рабочих | Число больных | Число рабочих | Число больных | |
| Мужчины | ||||
| Женщины | ||||
| Всего |
Вариант № 7
ЗадачаВычислить прямым методом стандартизованные показатели рождаемости в двух районах и сравнить их с показателями, вычисленными обычным путем. Сформулировать вывод.
| Возраст | Район А | Район Б | ||
| Число населения | Число родившихся | Число населения | Число родившихся | |
| До 19 лет | ||||
| 20 -29 лет | ||||
| 30 - 39 лет | ||||
| 40 и старше | ||||
| Всего |
Вариант № 8
ЗадачаВычислить прямым методом стандартизованные показатели рождаемости в двух районах и сравнить их с показателями, вычисленными обычным путем. Сформулировать вывод.
| Возраст | Район А | Район Б | ||
| Число населения | Число родившихся | Число населения | Число родившихся | |
| До 19 лет | ||||
| 20 -29 лет | ||||
| 30 - 39 лет | ||||
| 40 и старше | ||||
| Всего |