Проводимость твердых тел. Контактные явления

Лекция 4.

4.1. Фундаментальная система уравнений для полупроводников

Поскольку основными носителями заряда в полупроводниках являются свободные электроны и дырки, то их электропроводность (σ) определяется электропроводностью электронов и дырок

σ = σ_n+σ_p = qμ_nn + qμ_pp = q(μ_nn + μ_pp). (4.1)

Для чистого бездефектного кристалла, с проводимостью близкой к собственной, справедливо равенство n_i = p_i. Поэтому электропроводность беспримесного (собственного) полупроводника определяется равенством:

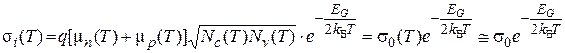
(4.2)

Как и в случае беспримесных полупроводниковых кристаллов, электропроводность легированных кристаллов складывается из электронной и дырочной проводимости:

.

Если n >> p, то s_n >>s_p , поэтому

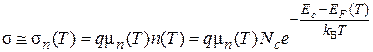. (4.3)

Если р >> п, то s_р >> s_п, поэтому

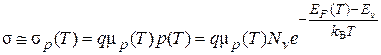. (4.4)

Во внешнем электрическом поле свободные носители заряда (электроны и дырки) начинают дрейфовать, вызывая появление тока. Кроме того, направленный перенос заряда возникает в форме диффузионного движения при неравновесных процессах, когда в объеме полупроводника появляются градиенты концентраций свободных носителей заряда.

Плотность дрейфового тока свободных электронов:

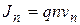, (4.5)

где q – заряд свободного носителя (электрона, q = 1,602×10^-19 Кл), п – концентрация свободных электронов, v_n – их средняя дрейфовая скорость.

Плотность дрейфового тока свободных дырок:

, (4.6)

где п – концентрация свободных дырок, v_р – их дрейфовая скорость.

Дрейфовые скорости электронов и дырок зависят от их подвижностей (m_п и m_р) и напряженности внешнего электрического поля (Е):

,

. (4.7)

В относительно слабом электрическом поле подвижности свободных носителей не зависят от напряженности этого поля. В таком случае появляется возможность характеристики проводящих свойств полупроводника с помощью параметра s, называемого удельной электропроводностью:

,

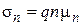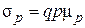. (4.8)

Иногда используют параметр, называемый удельным сопротивлением r, причем 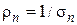и 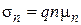. Таким образом, для дрейфовых плотностей тока можно записать равенства:

,

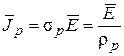. (4.9)

Диффузионные токи вызываются внутренними электрическими полями, возникающими в тех местах полупроводника, где под влиянием какого-то внешнего воздействия появляется градиент концентрации свободных носителей (электронов или дырок). Направление поля оказывается таким, что свободные носители будут перемещаться из области с более высокой концентрацией в область с меньшей концентрацией. При этом плотности диффузионных токов свободных электронов и дырок определяются следующими векторными равенствами:

,

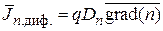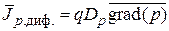, (4.10)

где коэффициенты диффузии свободных носителей заряда (D_n и D_p) связаны с их подвижностями,

,

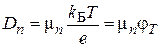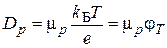, (4.11)

j _Т – тепловой потенциал.

Подвижности свободных носителей (m_п и m_р) зависят от температуры Т и от суммарной концентрации донорных и акцепторных атомов N=N_d+N_a:

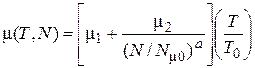, (4.12)

значения и характеристики некоторых констант, использованных в приведенных выше формулах, можно найти в таблицах 2.1 и 2.2.

Проводимость кристалла, содержащего несколько типов (k-типов) подвижных носителей заряда

, (4.13)

где 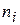- концентрация носителей заряда i-го вида, 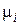- подвижность носителей заряда i-го вида, 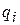- величина заряда свободного носителя i-го вида.

Величина, обратная к проводимости, называется удельным сопротивлением. Для полупроводника с р-типом проводимости удельное сопротивление равно:

, (4.14)

где N_a - концентрация акцепторных атомов, - заряд электрона, m_p - подвижность дырок. Удельное сопротивление полупроводника с п-типом проводимости равно:

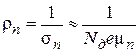, (4.15)

где N_d - концентрация донорных атомов, - заряд электрона, m_n - подвижность электронов.

Интегральные сопротивления полупроводниковых образцов с р- и п-типами проводимости можно найти по формулам

и 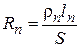, (4.16)

где l_p и l_n – длины образцов, S – площади поперечного сечения, а r_p и r_n – их удельные сопротивления.

В отсутствие сильных магнитных полей физические свойства полупроводника, связанные с его электрической проводимостью, описываются системой из пяти основных уравнений, называемой фундаментальной системой уравнений полупроводника:

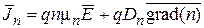, (4.17)

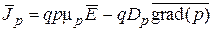, (4.18)

, (4.19)

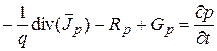, (4.20)

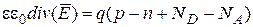, (4.21)

где уравнения (4.17) и (4.18) являются уравнениями для плотностей электронного и дырочного токов, (4.19) и (4.20) – уравнения нерпрерывности, (4.21) – уравнение Пуассона. В этих уравнениях использованы следующие дополнительные обозначения: R_p и R_n – число рекомбинировавших носителей заряда (дырок и электронов, соответственно) в единицу времени, G_p и G_n – число появившихся носителей заряда (дырок и электронов, соответственно) в результате их тепловой генерации в единицу времени. Эти величины связаны с временами жизни свободных носителей:

, . (4.22)