Краткие теоретические сведения. ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ПРИ

ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ПРИ

РАСТЯЖЕНИИ

Цель работы – определение модуля продольной упругости Е (модуля Юнга) материала испытуемого образца, опытная проверка закона Гука при растяжении.

Краткие теоретические сведения

Для проверки закона Гука и определения модуля упругости материала испытуемого образца необходимо измерение упругих деформаций при растяжении его в пределах пропорциональности.

Испытанию подвергают так называемые нормальные образцы круглого или прямоугольного сечения. Для получения сравниваемых результатов опытов форма, размеры и условия нагружения образцов должны определяться стандартом (ГОСТ 1497-84 «Металлы. Методы испытания на растяжение»). На рис. 1 показан пропорциональный цилиндрический образец типа I, используемый для испытания на растяжение.

Настоящий стандарт устанавливает методы статических испытаний на растяжение черных и цветных металлов и изделий из них номинальным диаметром или наименьшим размером в поперечном сечении 3,0 мм и более для определения при температуре характеристик механических свойств:

– предела пропорциональности;

– модуля упругости;

– предела текучести физического;

– предела текучести условного;

– временного сопротивления;

– относительного равномерного удлинения;

– относительного удлинения после разрыва;

– относительного сужения поперечного сечения после разрыва.

Стандарт не распространяется на испытания проволоки и труб.

Рис. 1

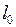Начальная расчетная длина пропорционального цилиндрического образца должна равняться (или , d – начальный диаметр образца). Рабочая длина образца принимается равной .

Большинство материалов, при растяжении или сжатии, подчиняются пропорциональной зависимости между приложенной нагрузкой и деформацией, вызываемой этой нагрузкой, т. е. они подчиняются закону Гука

где 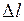– абсолютная продольная деформация (удлинение или укорочение) образца под действием силы Р, приложенной вдоль оси стержня; l – расчетная длина образца; F – площадь поперечного сечения образца; Е – модуль упругости первого рода (модуль Юнга), представляющий коэффициент пропорциональности между напряжением и деформацией и характеризующий способность материала сопротивляться упругим деформациям.

Зная размеры исследуемого образца, его деформацию и растягивающую силу, можно вычислить модуль упругости, используя формулу закона Гука

Чтобы убедиться в линейной зависимости между нагрузкой и удлинением при определении модуля упругости Е нагружение образца производят несколькими ступенями, при этом нагрузку каждый раз увеличивают на одну и ту же величину. После каждого нагружения измеряют абсолютное удлинение .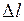

Приращение длины образца на одну и ту же величину подтверждает линейную зависимость между абсолютным удлинением образца 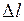и продольной силой Р, т.е. справедливость закона Гука.

Величина ступени нагружения зависит от материала образца и размеров его поперечного сечения; ее выбирают таким образом, чтобы наибольшая нагрузка при испытании не вызывала остаточных деформаций.