Основы теории напряженного состояния
Напряженное состояние в точке – совокупность напряжений, действующих во множестве площадок, проходящих через данную точку.
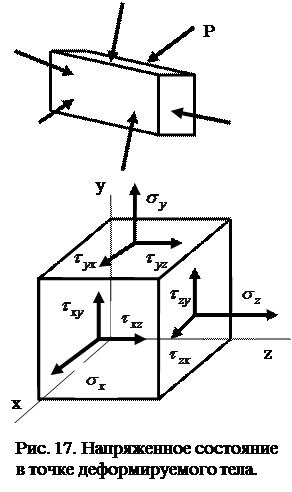
Исследуя напряженное состояние в данной точке деформируемого тела, в ее окрестностях выделяют бесконечно малый (элементарный) параллелепипед, ребра которого направлены вдоль соответствующих координатных осей.
При действии на тело внешних сил на каждой из граней элементарного параллелепипеда возникают напряжения, которые представляют нормальными и касательными напряжениями – проекциями полных напряжений на координатные оси.
Таким образом, на гранях элементарного параллелепипеда, выделенного в окрестности точки нагруженного тела, действует девять компонентов напряжения. Запишем их в виде матрицы, которая называется тензором напряжений
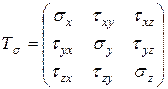 (3.10)
(3.10)
Не все девять компонентов напряжений, действующих на гранях параллелепипеда, независимые (несвязанные друг с другом). В этом легко убедиться, составив уравнения равновесия суммы моментов относительно координатных осей. Записав уравнения моментов от сил, действующих по граням параллелепипеда, и пренебрегая их изменением при переходе от одной грани к другой ей параллельной, получим, что
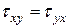 ,
, 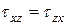 ,
, 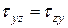
 Данные равенства называют законом парности касательных напряжений.
Данные равенства называют законом парности касательных напряжений.
Закон парности касательных напряжений: на взаимно перпендикулярных площадках действуют равные по величине и противоположно направленные касательные напряжения.
В окрестности исследуемой точки можно выделить бесконечное множество взаимно перпендикулярных площадок. В том числе можно найти такие площадки, по граням которых действуют только нормальные напряжения, а касательные напряжения равны нулю. Такие площадки называют главными.
Главные площадки – три взаимно перпендикулярные площадки в окрестности исследуемой точки, на которых касательные напряжения равны нулю.
Главные напряжения – нормальные напряжения, действующие по главным площадкам.
На главных площадках нормальные напряжения принимают свои экстремальные значения 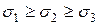
Тензор напряжений для главных площадок: 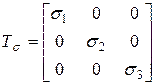 (3.11)
(3.11)
В зависимости от того, сколько главных напряжений действует в окрестности данной точки, различают три вида напряженного состояния:
1. Линейное (одноосное) – если одно главное напряжение отлично от нуля, а два других равны нулю ( 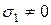 ,
, 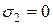 ,
, 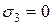 );
);
2. Плоское (двухосное) – если два главных напряжения отличны от нуля, а одно равно нулю ( 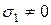 ,
, 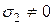 ,
, 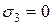 );
);
3. Объемное (трехосное) – если все три главных напряжения отличны от нуля ( 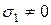 ,
, 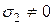 ,
, 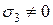 );
);
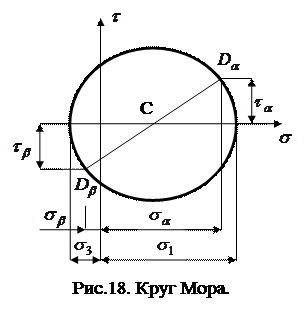 Напряженное состояние в точке при плоском напряженном состоянии можно описать с помощью круга Мора, построенного в координатных осях
Напряженное состояние в точке при плоском напряженном состоянии можно описать с помощью круга Мора, построенного в координатных осях 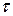 и
и 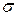 . Здесь
. Здесь 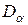 и
и 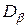 точки, соответствующие напряженному состоянию на любых двух взаимно перпендикулярных площадках
точки, соответствующие напряженному состоянию на любых двух взаимно перпендикулярных площадках 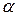 и
и 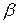 с координатами (
с координатами ( 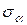 ;
; 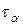 ) и (
) и ( 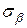 ;
; 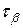 ) соответствен-но. Через эти две точки проводится окружность радиусом
) соответствен-но. Через эти две точки проводится окружность радиусом 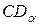 или
или 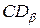 (точка С – центр круга Мора). В точках, где круг Мора пересекает ось
(точка С – центр круга Мора). В точках, где круг Мора пересекает ось 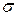 можно найти величину главных нормальных напряжений
можно найти величину главных нормальных напряжений 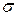 (так как касательные напряжения равны нулю.
(так как касательные напряжения равны нулю.
Теории прочности
Важнейшей задачей инженерного расчета является оценка прочности детали по известному напряженному состоянию. При сложном напряженном состоянии приходится вводить некоторый критерий прочности (гипотезу о преимущественном влиянии на прочность того или иного фактора), предельное значение этого фактора находят из опыта на растяжение.
