Определение напряжений и деформаций при кручении

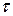Выведем формулу для определения касательных напряжений и найдем зависимость между углом закручивания и внутренним крутящим моментом. Данная задача применительно к валам круглого сечения может быть решена, если ввести соответствующие гипотезы, которые подтверждаются экспериментами.

Гипотезы, принимаемые при расчете на кручение:

- сечения, плоские до деформации, остаются плоскими, и после деформации (гипотеза Бернулли, гипотеза плоских сечений);

- все радиусы данного сечения остаются прямыми (не искривляются) и поворачиваются на один и тот же угол, то есть каждое сечение поворачивается относительно оси x как жесткий тонкий диск;

- расстояния между сечениями при деформации не изменяются.

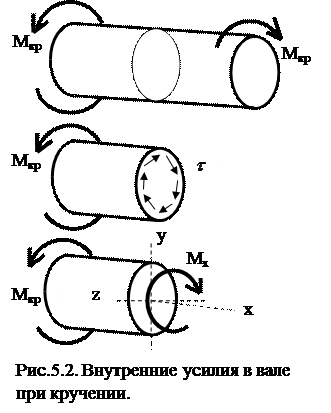
Поскольку крутящий момент М_x – единственный внутренний силовой фактор в поперечном сечении, действующий при этом в плоскости данного сечения, можно предположить, что при кручении в поперечных сечениях вала возникают только касательные напряжения (на основе интегральных уравнений равновесия).

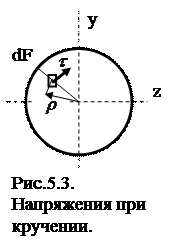
В сечении вала выделим элементарную площадку dF на расстоянии 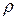от продольной оси (ось x) стержня. При кручении на площадке dF, будут действовать касательные напряжения 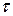, которые создадут элементарный крутящий момент dM, относительно оси x:

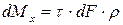, (5.1)

Тогда полный момент, возникающий во всем сечении, найдем как

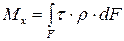, (5.2)

где 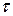- касательное напряжение, действующее на элементарной площадке dF, расположенной на произвольном расстоянии (радиусе) 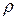от центра сечения.

Перпендикулярность вектора касательных напряжений радиусу объясняется отсутствием на поверхности вала касательных напряжений, параллельных его оси, и, соответственно (по закону парности касательных напряжений), отсутствием касательных напряжений вдоль радиуса.

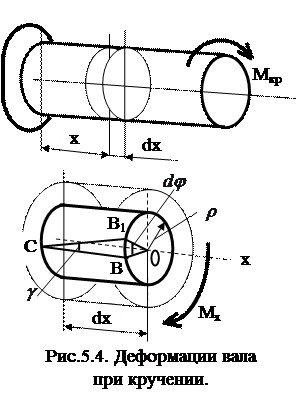
Рассмотрим деформацию элемента стержня (вала) длиной dx, выделенного из закручиваемого стержня в произвольной точке с координатой x.

Условно примем, что левое сечение элемента dx остается неподвижным, а правое поворачивается на угол 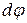, создаваемый за счет закручивания вала на длине dx. Один из радиусов ОB, оставаясь прямым, поворачивается вместе с сечением на угол 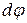, при этом точка В переходит в положение В₁, а образующая СВ в положение CB₁, поворачиваясь на угол 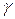– угол сдвига в этой точке вала.

Длину дуги BB₁, найдем из рассмотрения треугольников OBB₁ и CBB₁:

,

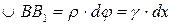следовательно

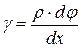(5.3)

Запишем закон Гука, связывающий касательные напряжения с углом сдвига

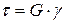. (5.4)

Подставим выражение (5.3) в формулу (5.4):

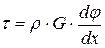, (5.5)

а полученное выражение (5.5) – в формулу (5.2):

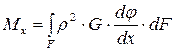. (5.6)

Так как в полученном выражении (5.6) величины G и 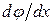, в соответствии с принятыми гипотезами, остаются постоянными по данному сечению, то их можно вынести за знак интеграла:

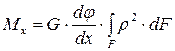. (5.7)

Величина 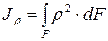– называется полярным моментом инерции и является геометрической характеристикой данного сечения. Таким образом, окончательно можем записать

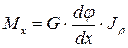, (5.8)

или, подставляя (5.5) в (5.7),

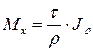. (5.9)

Величина касательных напряжений при кручении определяется следующим образом:

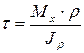(5.10)

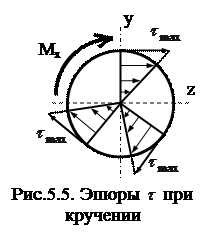
Как видно, касательные напряжения распределены по сечению вала по линейному закону и достигают максимальной величины на поверхности вала (при ):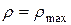

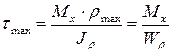, (5.11)

где 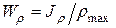– полярный момент сопротивления.

Величина 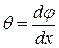называется относительным (погонным)углом закручивания и имеет размерность рад/м.

Используя выражение (5.8), найдем формулу для определения относительного угла закручивания:

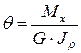(5.12)

Зная формулы для определения относительного угла закручивания, можно записать формулу для определения взаимного угла поворота двух сечений, расположенных на расстоянии 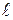друг от друга:

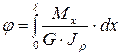(5.13)

Если в пределах участка длиной 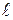крутящий момент и геометрические характеристики сечения вала остаются постоянными, то угол закручивания можно определить как

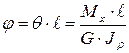. (5.14)