Определение внутренних усилий и напряжений при сдвиге

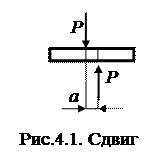Сдвиг – вид сопротивления, при котором стержень нагружен двумя равными силами (на малом расстоянии друг от друга), перпендикулярными к оси бруса и направленными в противоположные стороны.

Примером такого действия сил на брус может быть разрезание ножницами прутьев, деформация заклепок, болтов, сварных швов между металлическими листами и т. п.

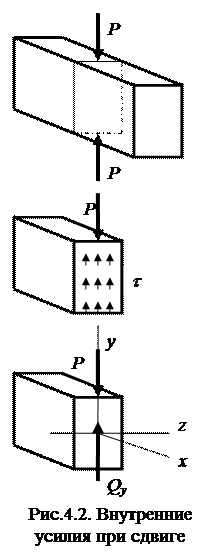
Мысленно рассекая брус поперечным сечением перпендикулярным продольной оси определим внутренние усилия, действующие в сечении бруса при сдвиге.

В данном случае нагружения из шести уравнений равновесия лишь одно не нулевое: 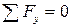, следовательно .

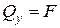При сдвиге в сечении элемента возникает только одно внутреннее усилие – поперечная сила ( 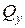или ).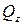

Так как единственное внутреннее усилие, возникающие при сдвиге (поперечная сила 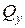или 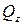), лежит в плоскости поперечного сечения, то и напряжения, лежат в плоскости сечения стержня. То есть при сдвиге в точках поперечного сечения стержня возникают только касательные напряжения .

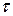Таким образом, поперечная сила, возникающая в сечении

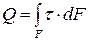. (4.1)

При сдвиге считают, что касательные напряжения равномерно распределены по площади поперечного сечения, т.е. 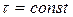, поэтому

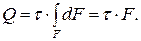(4.2)

Касательные напряжения при сдвиге определяются по формуле 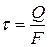, а так как 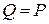, то

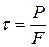. (4.3)

Напряженное состояние при сдвиге

Чистый сдвиг – частный случай плоского напряженного состояния, при котором по граням прямоугольного элемента действуют только касательные напряжения.

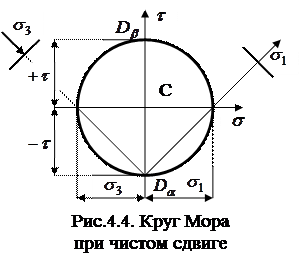
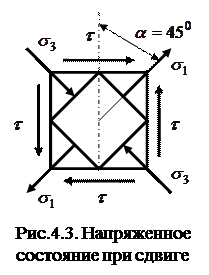Построим круг Мора: Точк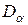и и 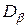точки, соответствующие напряженному состоянию на указанных взаимно перпендикулярных площадках 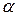и 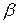с координатами ( 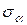; 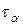) т.е. (0; - 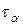) и ( 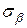; 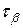) т.е. (0; 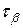) соответственно ( 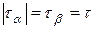). Через эти две точки проводится окружность радиусом 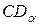или 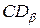(точка С – центр круга Мора). В точках где круг Мора пересекает ось можно найти величину главных нормальных напряжений 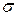(так как касательные напряжения равны нулю.

Определим величину и направление главных напряжений при чистом сдвиге:

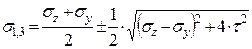,(4.4)

так как 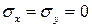, можно записать 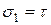и

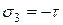
Направление главных площадок определяется углом 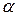, который найдем по формуле:

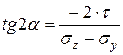; (4.5)

учитывая что ,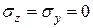

;

; .

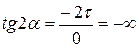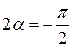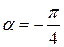Деформации при сдвиге

Рассмотрим деформацию квадратного элемента при сдвиге.

Рис.4.5. Деформация квадратного элемента при сдвиге.

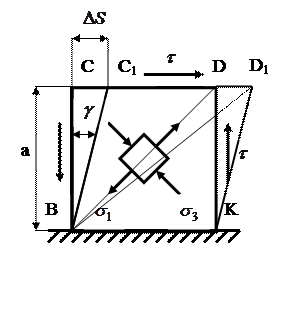Поскольку по граням элемента не действуют нормальные напряжения, то вдоль граней нет и удлинений. В то же время диагональ BD, совпадающая с направлением , удлинится, а диагональ СК, совпадающая с направлением сжимающего напряжения 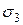, укоротиться. В результате квадрат BCDK трансформируется в ромб BC₁D₁K, без изменения длины граней. Таким образом, деформация сдвига характеризуется изменением первоначально прямых углов.

Малый угол 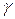, на который изменяется первоначально прямой угол элемента при сдвиге, называется
углом сдвига или относительным сдвигом.

Величину абсолютного смещения грани обозначают 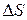и называют абсолютным сдвигом.

Из прямоугольного треугольника ВСС₁:

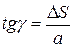(4.6)

Учитывая малость угла можно считать, что 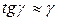, тогда окончательно запишем взаимосвязь между относительным и абсолютным сдвигом элемента

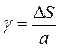(4.7)

При сдвиге можно экспериментально построить диаграмму сдвига, аналогичную диаграмме растяжения, на которой также в начале нагружения будет прямолинейный участок деформации по закону Гука.

Закон Гука при сдвиге:

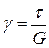или 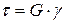, (4.8)

где G – модуль касательной упругости или модуль сдвига (модуль упругости второго рода), которая является константой для данного материала.

Закон Гука при сдвиге через абсолютные деформации:

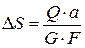, (4.9)

где а – расстояние между сдвигаемыми гранями; F – площадь грани.

Взаимосвязь между упругими постоянными:

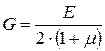. (4.10)