Прямоугольное отверстие в непрозрачном экране

Интегральные преобразования оптических сигналов

1) Определить спектр пространственных частот оптического сигнала, записанного на оптический транспарант с функцией пропускания ,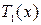

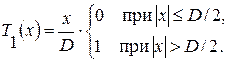
где D = 15 мм – апертура транспаранта, в схеме оптического процессора, осуществляющего преобразование Фурье, на длине волны l = 0,63 мкм и имеющего линзу с фокусным расстоянием F = 35 мм.

2) Определить энергию, сосредоточенную в основном лепестке и боковых лепестках спектра оптического сигнала.

3) Представить схему оптического процессора, графики исходного сигнала и его спектра.

4) Рассчитать дифракционные картины Фраунгофера для различных типов отверстий.

Расчет спектра сигнала

Исходные данные:

- Длина волны λ, мкм: 0,63;

- Фокусное расстояние линзы F, мм: 35;

- Апертура транспаранта D, мм: 15.

Зададим сигнал на входе транспаранта:

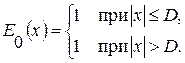
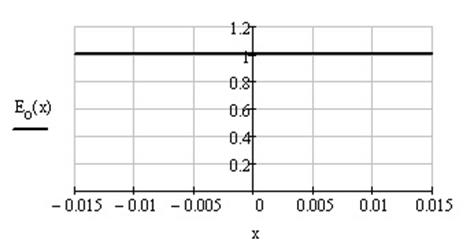
Рисунок 1.1 – Сигнал на входе транспаранта

Функция пропускания транспаранта:

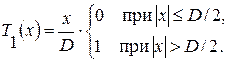
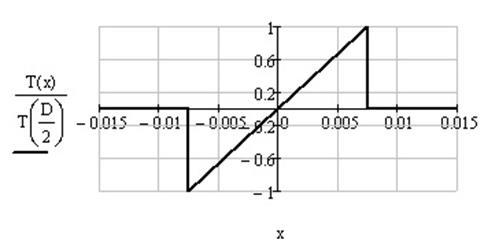
Рисунок 1.2 – Функция передачи транспаранта

Запишем сигнал на выходе транспаранта:

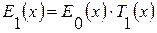
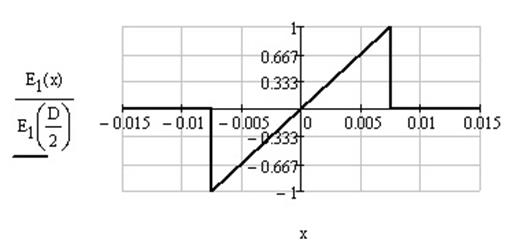
Рисунок 1.3 – Сигнал на выходе транспаранта

Определим спектр сигнала, используя преобразование Фурье:

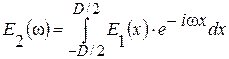
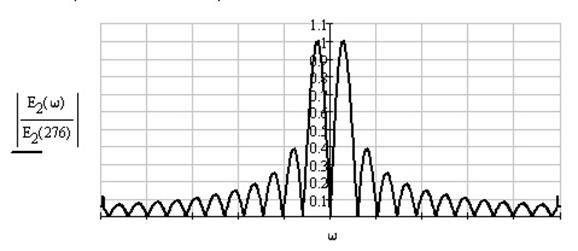
Рисунок 1.4 – Спектр сигнала

Определим энергию спектра:

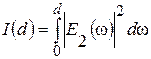
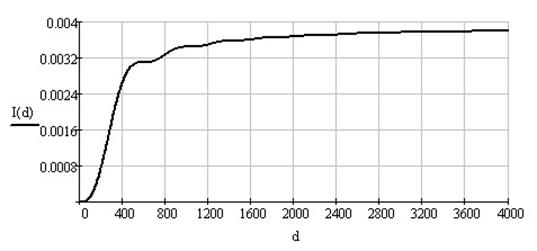
Рисунок 1.5 – Энергия спектра сигнала

Рассчитаем энергию, сосредоточенную в основном и боковых лепестках:

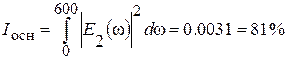
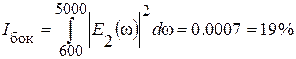
Схема оптического процессора представлена на рисунке 1.6.

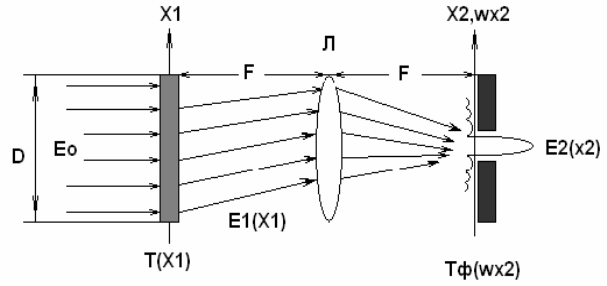
Рисунок 1.6 – Схема оптического процессора

Световая волна Е₀ падает на транспарант с функцией пропускания T(Х1). Линза выполняет преобразование Фурье и фокусирует световой пучок на экране, откуда с помощью анализатора спектра получаем информацию о сигнале.

Расчет дифракционных картин Фраунгофера для различных типов отверстий

Прямоугольное отверстие в непрозрачном экране

Получим выражение для интенсивности света в дифракционной картине:

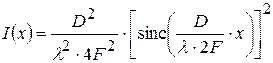
Распределение нормированной интенсивности света при дифракции Фраунгофера на прямоугольном отверстии, представленное на рис.1.7, имеет характерные признаки: ширина главного лепестка равна ∆х=4λF/D, максимальная интенсивность в первом дифракционном максимуме составляет около 4% от интенсивности в центре главного максимума.

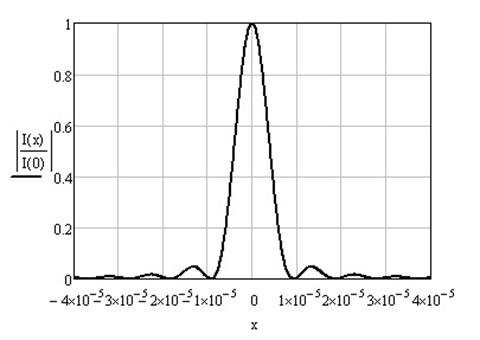
Рисунок 1.7 – Распределение интенсивности света вдоль координаты х при дифракции Фраунгофера на прямоугольном отверстии

при F = 35 мм, D = 15 мм

Проведем исследование. Выясним, как зависит спектр от фокусного расстояния и размеров отверстия

При F = 30 мм, D = 1 мм.

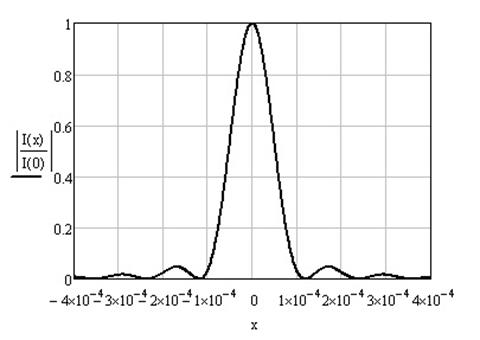
Рисунок 1.8 – Распределение интенсивности света вдоль координаты х при дифракции Фраунгофера на прямоугольном отверстии

при F = 30 мм, D = 1 мм

При F = 10 мм, D = 3 мм.

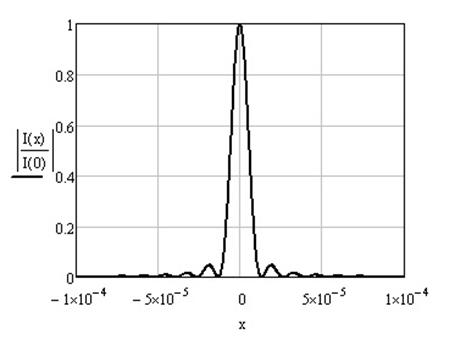
Рисунок 1.9 – Распределение интенсивности света вдоль координаты х при дифракции Фраунгофера на прямоугольном отверстии

при F = 10 мм, D = 3 мм