Расчет «максимального» и «минимального» магнитных моментов наночастиц и их диаметра
Для того чтобы частицы не выпадали в осадок скорость теплового движения частиц должна быть больше скорости оседания, определяемой формулой Стокса. Отсюда верхняя оценка размеров взвешенной частицы:
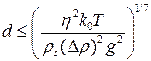 , (3.14)
, (3.14)
где 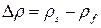 - разность плотностей твердой и жидкой фаз.
- разность плотностей твердой и жидкой фаз.
В зависимости от вязкости жидкости η формула (3.14) дает при комнатных температурах dmax~ 10-5 – 10-6 м. Практически в устойчивых коллоидах размеры частиц лежат в пределах 10-9 – 10-6 м.
В состоянии термодинамического равновесия распределение частиц по высоте подчиняется барометрическому закону:
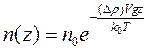 , (3.15)
, (3.15)
где V- объем частицы.
При сравнении численного значения объемной концентрации φ, полученной по плотности компонент системы φρ и по намагниченности насыщения φМ ≡MS/MS0 , оказывается, что φМ / φρ ≈ 0,7. Одной из причин такого расхождения является некоторое уменьшение размера магнитного ядра частиц в результате реакции адсорбции молекул ПАВа - олеиновой кислоты с поверхностью частиц магнетита Fe3O4. В результате образуется олеат железа, который не обладает магнитными свойствами. Благодаря этому «магнитный диаметр» каждой частицы уменьшается на величину удвоенную толщину немагнитного слоя ε=0,83 нм (постоянная кристаллической решетки магнетита).
Понятие суперпарамагнетизм введено в 1938 г. Элмором (W.C. Elmore). Его эксперименты положили начало магнитной гранулометрии – методу измерения размеров и магнитных моментов мелких частиц по кривой намагничивания. В реальной дисперсной системе существует распределение частиц по магнитным моментам и линейным размерам. Получаемые путем сравнения кривой намагничивания с идеальной ланжевеновской зависимостью оценки параметров наночастиц физически и количественно различны между собой, поскольку для их получения используются начальный и конечный участки кривой намагничивания. Начальный участок кривой намагничивания в основном формируется частицами с наибольшим магнитным моментом, а участок окрестности магнитного насыщения – частицами с относительно малым магнитным моментом.
Поэтому условно можно ввести понятия «максимальном» и «минимальном» магнитных моментов наночастиц.
Максимальные и минимальные магнитные моменты частиц 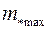 ,
, 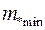 полученные на основе магнитогранулометрического метода, в соответствии с теорией суперпарамагнетизма рассчитываются по формулам:
полученные на основе магнитогранулометрического метода, в соответствии с теорией суперпарамагнетизма рассчитываются по формулам:
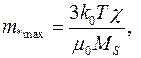 (3.15)
(3.15)
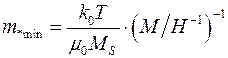 , (3.16)
, (3.16)
где 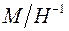 - тангенс угла наклона прямолинейного участка кривой
- тангенс угла наклона прямолинейного участка кривой 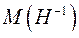 при
при 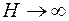 .
.
Магнитный момент наночастицы может быть представлен также в виде:
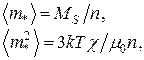 (3.17)
(3.17)
где n концентрация частиц.
Размер частиц (диаметр – в предположении их сферической формы) определяется из выражения:
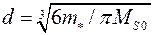 = 0,016
= 0,016 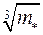 , (3.18)
, (3.18)
где 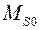 - намагниченность насыщения дисперсной фазы (
- намагниченность насыщения дисперсной фазы ( 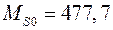 кА/м для магнетита).
кА/м для магнетита).
Магнитный момент феррочастицы выражается через намагниченность насыщения ферромагнетика MSO:
m*=MSO·Vf,
где Vf – объем магнитной части частицы.
Если «магнитное ядро» частицы магнетита имеет форму шара диаметром d, то 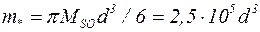 . При d=10 нм m*=2,5·10-19 А·м2.
. При d=10 нм m*=2,5·10-19 А·м2.
ЗАДАЧА:Рассчитать напряженность магнитного поля Н, при которой потенциальная энергия магнитной наночастицы в магнитном поле равна кинетической энергии поступательного движения частицы в звуковой волне.
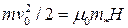 ;
; 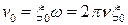 ;
; 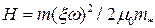
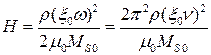 ;
;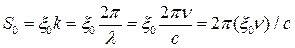 ;
;
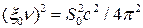 ;
; 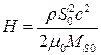 .
.
Проверить размерность полученного выражения для Н и произвести расчет для случая S0=10-4. ρ=5,25·103кг/м3, 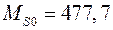 кА/м, с=103м.
кА/м, с=103м.
--------------------------------------------------------------------------------
Аналогичная задача для эллипсоидальных частиц (линейных кластеров):
На тело, обтекаемое однородным потоком идеальной, несжимаемой жидкости, действует момент сил равный [18]:
Mr=- 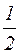 (λ||-λ ^)U2 sin2q,
(λ||-λ ^)U2 sin2q,
где λ|| и λ^ – компоненты тензора присоединенных масс эллипсоида, U – скорость обтекающего потока, q – угол между направлением скорости U и большой осью эллипсоида.
Эффективность вращательного воздействия потока жидкости на агрегаты по сравнению с воздействием теплового броуновского движения и магнитного поля достаточно мала.
Используя выражения λ|| и λ^ для эллипсоида вращения с большой и малой полуосями 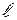 и d, по порядку величины получим [18]: Mr ~ (4/3)p
и d, по порядку величины получим [18]: Mr ~ (4/3)p 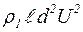 . Магнитный момент эллипсоида находим по формуле
. Магнитный момент эллипсоида находим по формуле
m=m*Nag= 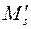 Nag 4p
Nag 4p 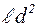 /3,
/3,
где Nag – число ферромагнитных частиц в агрегате, m* – магнитный момент одной ферромагнитной частицы, 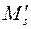 – намагниченность ферромагнитных частиц.
– намагниченность ферромагнитных частиц.
Оценим величину магнитного поля, при котором удовлетворяется равенство 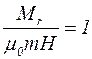 . Составим отношение
. Составим отношение
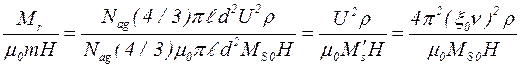 .
.
Для ультразвука мощностью 1 Вт/см2 при частоте ν=1 МГц амплитуда смещения порядка 2·10-8 м. Это соответствует амплитуде колебательной скорости U=0,13 м/с. Полагая 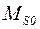 ~4,7·105 А/м, получим что Mr=µ0m*H при H»20 А/м.
~4,7·105 А/м, получим что Mr=µ0m*H при H»20 А/м.
Оценим объем эллипсоидальной частицы, имеющей в потоке звуковой волны энергию, сопоставимую с энергией теплового броуновского движения (U~0,02 м/с, Т~300 К)
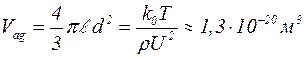 .
.
Принимая по порядку величин 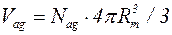 (Rm – радиус одной ферромагнитной частицы), получим оценку числа частиц в агрегате Nag: Nag≈2·104.
(Rm – радиус одной ферромагнитной частицы), получим оценку числа частиц в агрегате Nag: Nag≈2·104.
