Тема 3. Расчеты на прочность и жесткость при растяжении – сжатии. Определение напряжений, напряженное состояние, испытание на растяжение. Условия прочности и жесткости
Нормальные и касательные напряжения в поперечном сечении стержня. Абсолютная и относительная деформация
Прежде чем исследовать особенности напряженно – деформированного состояния стержня при растяжении – сжатии целесообразно сформулировать основные понятия, которые будут использованы в данной теме.
Продольная ось бруса (стержня) – непрерывная линия, проходящая через центры тяжести (центры площади) поперечных сечений бруса.
Поперечное сечение бруса (стержня) - сечение бруса плоскостью, перпендикулярной продольной оси бруса.
Волокно – (понятие вводится для повышения наглядности) цепочка частиц деформируемого тела. Продольные волокна параллельны продольной оси стержня. Реальные волокна существуют в волокнистых материалах, например, дереве. Воображаемые волокна помогают представить картину деформирования.
Центральное растяжение стержня – вид нагружения и деформирования стержня, при котором все внешние силы действуют вдоль его продольной оси.
Продольная интегральная сила N является суммой распределенных внутренних сил, действующих в данном поперечном сечении площадью F
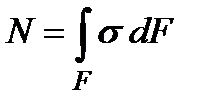 . (3.1)
. (3.1)
Если нормальную силу N можно найти, составляя уравнения равновесия для отсеченной части стержня согласно методу сечений (рис.3.1б,в, сечение I-I), то нормальные напряжения σ в каждой точке сечения из соотношения (3.1) найти нельзя, так как в общем случае неизвестно, как они распределены по площади сечения.
Рис. 3.1. Центральное растяжение стержня
Рассмотрим стержень длиной l, на который в общем случае действует сложная система внешних сил: сосредоточенных и направленных вдоль продольной оси (Р1, Р4, Р5, Р6); распределенных q3, действующих на участке длиной l3; сосредоточенных, которые приложены в одной точке продольной оси (Р21, Р22) и направлены под некоторым углом α к этой оси. В последнем случае силы должны быть равны по величине, чтобы сумма их проекций на поперечную ось равнялась нулю.
Для вычисления нормальных напряжений σ в сечении необходимо знать характер их распределения по сечению. При решении данной задачи применяется обоснованная экспериментальными данными гипотеза плоских сечений (Бернулли). Установлено, что ортогональная система рисок (рис. 3.2а), нанесенная на стержень до нагружения, при малых деформациях остается ортогональной и после его нагружения (рис. 3.2б). Значит, поперечные сечения остаются плоскими и перпендикулярными продольной оси стержня, а продольные волокна не взаимодействуют между собой (остаются прямыми и параллельными оси) и удлиняются на одну и ту же величину. Ортогональность продольных и поперечных рисок свидетельствует также об отсутствии сдвигов, а следовательно, и связанных с ними касательных напряжений τ в поперечных и продольных сечениях стержня. При этом можно утверждать, что при центральном растяжении – сжатии нормальные напряжения σ равномерно распределены по сечению. Однако следует учитывать, что такой характер распределения нормальных напряжений (гипотеза Сен-Венана) справедлив лишь на некотором удалении от точки приложения внешней силы.
Рис. 3.2. Гипотеза плоских сечений
Тогда нормальные напряжения в текущем сечении стержня с координатой z (ось Oz совпадает с продольной осью стержня) при центральном растяжении – сжатии равны
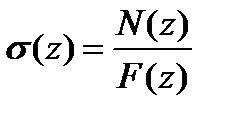 , (3.2)
, (3.2)
где F(z) – площадь поперечного сечения стержня в текущем сечении z. При растяжении σ>0, а при сжатии σ<0.
Рассмотрим подробнее изменение напряжений в сечениях стержня, которые не перпендикулярны его продольной оси, на так называемых наклонных площадках.
Определение напряжений на наклонных площадках при растяжении – сжатии стержня
Рассмотрим однородный растянутый стержень (рис.3.3а), в поперечных сечениях которого действуют равномерно распределенные напряжения  . Проведем произвольную секущую плоскость а-б, которая наклонена по отношению к поперечному сечению стержня на угол
. Проведем произвольную секущую плоскость а-б, которая наклонена по отношению к поперечному сечению стержня на угол 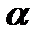 . Определим напряжения, действующие в этой наклонной плоскости. Очевидно, что полное напряжение р на данной площадке, согласно условию однородности, будет постоянным в любой точке площадки.
. Определим напряжения, действующие в этой наклонной плоскости. Очевидно, что полное напряжение р на данной площадке, согласно условию однородности, будет постоянным в любой точке площадки.
Рис. 3.3. Напряжения на наклонных площадках
Равнодействующая внутренних сил в сечении должна быть направлена по оси стержня и равна растягивающей силе в поперечных сечениях, т.е.
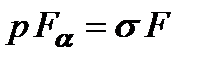 ,
,
где 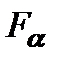 - площадь наклонного (косого) сечения, причем
- площадь наклонного (косого) сечения, причем 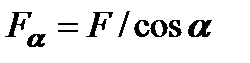 . Тогда полное напряжение на наклонной площадке равно
. Тогда полное напряжение на наклонной площадке равно 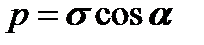 . Раскладывая это напряжение по нормали и по касательной к наклонной площадке (рис. 3.3б, в), находим
. Раскладывая это напряжение по нормали и по касательной к наклонной площадке (рис. 3.3б, в), находим
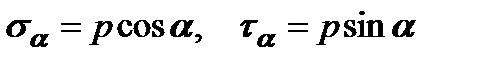
или, учитывая 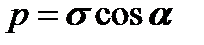 , имеем
, имеем
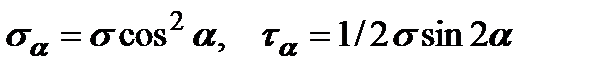 . (3.3)
. (3.3)
Видно, что в одной и той же точке А растянутого стержня значения возникающих в сечении напряжений оказываются различными в зависимости от ориентации наклонной площадки (угол α). Поэтому утверждение о том, что при растяжении – сжатии стержня возникают только нормальные напряжения не корректно, это справедливо только для поперечных сечений. Анализ формул (3.3) показывает, что в поперечных сечениях стержня (α=0°) нормальные напряжения достигают максимального значения, а касательные равны нулю. В продольных сечениях (α=90°) и нормальные, и касательные напряжения равны нулю. Касательные напряжения достигают максимального значения τmax=σ/2 на площадках, наклоненных под углом 45° к поперечному сечению стержня.
Выделим в растянутом стержне (рис. 3.4) прямоугольник ABCD, причем стержень представляет собой пластину толщиной h. Нормальные и касательные напряжения, действующие по граням данного прямоугольника, определяются формулами (3.3). Причем для вычисления напряжений на гранях АВ и CD в формулу (3.3) необходимо подставить угол α, а для вычислений напряжений по граням ВС и DA угол α+90°. Важно отметить, что переход от произвольной площадки, наклоненной на угол α, к площадке, наклоненной на угол α+90° не сказывается на абсолютном значении касательных напряжений, а изменяет лишь их направление.
Рис.3.4. К закону парности касательных напряжений
Действительно,
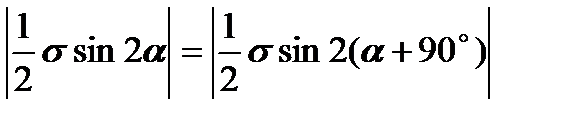 .
.
Следовательно, на двух взаимно перпендикулярных площадках (если не учитывать знаки) касательные напряжения должны быть равны. Это условие носит название закона парности касательных напряжений. Данное утверждение можно доказать составив уравнения равновесия прямоугольника ABCD, так для касательных напряжений имеем τAB=τCD и τBС=τDА. Очевидно, что пары моментов от касательных напряжений тоже должны быть уравновешены
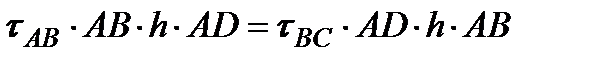 .
.
Таким образом, 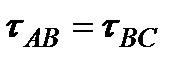 , что и требовалось доказать. Кроме того, следует обратить внимание, что касательные напряжения на двух взаимно перпендикулярных площадках направлены либо оба к общему ребру А и С, либо от ребра B и D.
, что и требовалось доказать. Кроме того, следует обратить внимание, что касательные напряжения на двух взаимно перпендикулярных площадках направлены либо оба к общему ребру А и С, либо от ребра B и D.
Деформированное состояние растянутого (сжатого) стержня
Рассмотрим брус длиной l и шириной b до нагружения (рис. 3.5а) и после нагружения силой Р (рис. 3.5б). Абсолютное продольное удлинение (деформация) стержня равно Δl. При растяжении Δl>0, при сжатии Δl<0. Если найти отношение абсолютного удлинения стержня к его исходной длине, то получим относительную продольную деформацию стержня Δl / l= εпрод. Очевидно, что при растяжении εпрод>0, при сжатии εпрод<0. Одновременно с продольным удлинением стержня для большинства материалов характерно изменение его поперечного сечения, где Δb – абсолютная поперечная деформация, причем при сжатии Δb>0, при растяжении Δb<0. Отношение Δb / b = εпопер называется относительной поперечной деформацией.
Рис. 3.5. Продольная и поперечная деформации стержня
Эксперимент показывает, что при малых деформациях растяжения - сжатия выполняется закон Гука в виде:
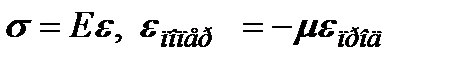 ,
,
где E - модуль Юнга (модуль упругости первого рода), µ - коэффициент Пуассона (для основных конструкционных материалов - µ = 0,3…0,4). Модуль Юнга и коэффициент Пуассона являются важнейшими механическими характеристиками материала, из которого изготовлен стержень и определяются опытным путем. Таким образом, если относительное продольная деформация постоянно по сечению, то и напряжение постоянно по сечению стержня 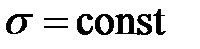 , и тогда из соотношения (3.1) сразу получаем:
, и тогда из соотношения (3.1) сразу получаем:
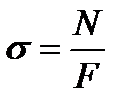 . (3.4)
. (3.4)
Формула (3.4) является основной для расчета на прочность при центральном растяжении (сжатии).
Относительная деформация (далее индекс «продольная» опускаем) в сечении стержня по закону Гука
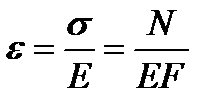 .
.
Произведение EF называют жесткостью стержня на растяжение.
Если на некотором участке стержня длиной l продольная сила постоянна, то постоянна и деформация. Т.к. по определению линейной деформации 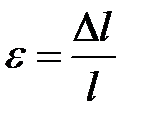 , то
, то
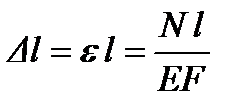 . (3.5)
. (3.5)
Для стержня, состоящего из ряда участков с постоянной жесткостью (EF)i и продольной силой Ni, производится суммирование по участкам:
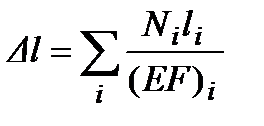 . (3.5’)
. (3.5’)
В самом общем случае сумма, очевидно, заменяется интегралом по всей длине стержня:
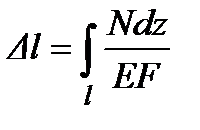 , (3.6)
, (3.6)
где координата z отсчитывается вдоль оси стержня.
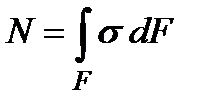 . (3.1)
. (3.1)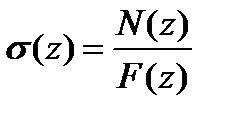 , (3.2)
, (3.2) . Проведем произвольную секущую плоскость а-б, которая наклонена по отношению к поперечному сечению стержня на угол
. Проведем произвольную секущую плоскость а-б, которая наклонена по отношению к поперечному сечению стержня на угол  . Определим напряжения, действующие в этой наклонной плоскости. Очевидно, что полное напряжение р на данной площадке, согласно условию однородности, будет постоянным в любой точке площадки.
. Определим напряжения, действующие в этой наклонной плоскости. Очевидно, что полное напряжение р на данной площадке, согласно условию однородности, будет постоянным в любой точке площадки.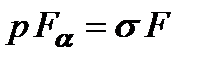 ,
,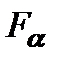 - площадь наклонного (косого) сечения, причем
- площадь наклонного (косого) сечения, причем 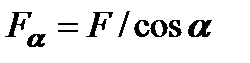 . Тогда полное напряжение на наклонной площадке равно
. Тогда полное напряжение на наклонной площадке равно 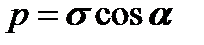 . Раскладывая это напряжение по нормали и по касательной к наклонной площадке (рис. 3.3б, в), находим
. Раскладывая это напряжение по нормали и по касательной к наклонной площадке (рис. 3.3б, в), находим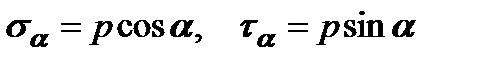
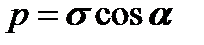 , имеем
, имеем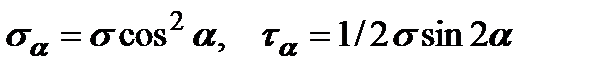 . (3.3)
. (3.3)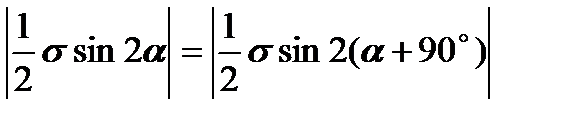 .
.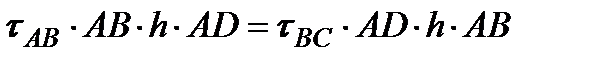 .
.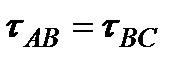 , что и требовалось доказать. Кроме того, следует обратить внимание, что касательные напряжения на двух взаимно перпендикулярных площадках направлены либо оба к общему ребру А и С, либо от ребра B и D.
, что и требовалось доказать. Кроме того, следует обратить внимание, что касательные напряжения на двух взаимно перпендикулярных площадках направлены либо оба к общему ребру А и С, либо от ребра B и D.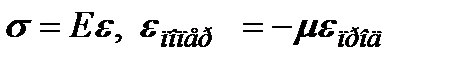 ,
,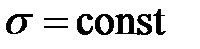 , и тогда из соотношения (3.1) сразу получаем:
, и тогда из соотношения (3.1) сразу получаем: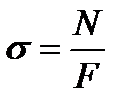 . (3.4)
. (3.4)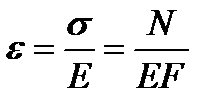 .
.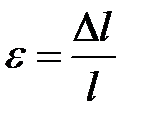 , то
, то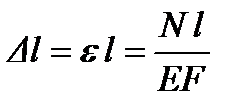 . (3.5)
. (3.5)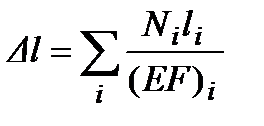 . (3.5’)
. (3.5’)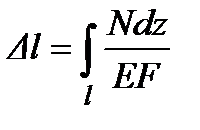 , (3.6)
, (3.6)