Дифракция в расходящихся лучах от круглого отверстия (дифракция Френеля)
Работа № 3. ДИФРАКЦИЯ
Цель работы: научиться получать дифракционные картины от различных объектов в расходящихся лучах, определять длину волны света по картине дифракции.
Вопросы, знание которых обязательно
для допуска к выполнению работы:
1. В чем заключается явление дифракции света?
2. Принцип Гюйгенса-Френеля.
3. Метод зон Френеля.
4. Как по виду дифракционной картины, получаемой от круглого отверстия, можно определить число зон Френеля?
5. В чем отличие дифракции Фраунгофера от дифракции Френеля?
6. Дифракция в расходящихся и параллельных лучах от круглого экрана и круглого отверстия.
7. Каков порядок следования цветов в дифракционных спектрах? Какова окраска нулевого максимума?
8. Что называют зонной пластинкой?
ВВЕДЕНИЕ
Дифракцией называется явление отклонения светового луча от прямолинейного распространения или огибания светом непрозрачных объектов. После дифракции, отклонившиеся от прямолинейного распространения, лучи могут встречаться и налагаться друг на друга, а в виду того, что они получены из одной волны, они являются когерентными (см. работу по интерференции света) и, следовательно, образуют интерференционную картину (чередование максимумов и минимумов излучения). Такую картину называют «дифракционной картиной». Для анализа такой картины необходимо знать амплитуды и фазы встречающихся волн.
Рассмотрим дифракция в расходящихся лучах (дифракция Френеля) и дифракция в параллельных лучах (дифракция Фраунгофера).
Дифракция в расходящихся лучах от круглого отверстия (дифракция Френеля)
 |
 Амплитуды колебаний, пришедших в точку А от различных участков волновой поверхности (рис.1), зависят от расстояния (b) этих участков до точки А, их величины и угла a между нормалью к
Амплитуды колебаний, пришедших в точку А от различных участков волновой поверхности (рис.1), зависят от расстояния (b) этих участков до точки А, их величины и угла a между нормалью к фронту волны и направлением на точку А. При нахождении результирующей амплитуды колебаний от всех участков необходимо учитывать еще и то, что фазы отдельных колебаний могут не совпадать, так как различны их пути до точки А. Нахождение амплитуды колебаний, в общем случае довольно сложная задача. Френель предложил простой метод, применение которого дает качественно правильную картину дифракции в ряде простейших случаев.
При разности хода волн 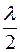 (
( 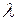 – длина волны) колебания происходят в противофазе и гасят друг друга. Френель предложил разбить волновой фронт на зоны, крайние точки которых дают колебания в противофазе, эта зона – часть шаровой поверхности на волновом фронте.
– длина волны) колебания происходят в противофазе и гасят друг друга. Френель предложил разбить волновой фронт на зоны, крайние точки которых дают колебания в противофазе, эта зона – часть шаровой поверхности на волновом фронте.
Зоны Френеля строятся следующим образом. Центральная зона (рис.1) включает все точки, разность фаз колебаний от которых в точке А не превышает p (расстояние которых до точки А не более b1 = 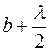 , где b – кратчайшее расстояние от волнового фронта до точки А). Соседняя вторая зона (при разности хода
, где b – кратчайшее расстояние от волнового фронта до точки А). Соседняя вторая зона (при разности хода 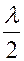 ) представляет кольцевую область на сфере, заключенную между точками, для которых
) представляет кольцевую область на сфере, заключенную между точками, для которых 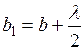 , с одной стороны, и
, с одной стороны, и 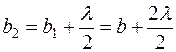 , с другой стороны. Очевидно, что следующие зоны будут также кольцевыми, ограниченными снаружи точками, для которых
, с другой стороны. Очевидно, что следующие зоны будут также кольцевыми, ограниченными снаружи точками, для которых 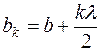 , где k – номер зоны. Можно показать, что площади всех зон приблизительно равны, а радиус k-ой зоны равен
, где k – номер зоны. Можно показать, что площади всех зон приблизительно равны, а радиус k-ой зоны равен
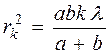 . (1)
. (1)
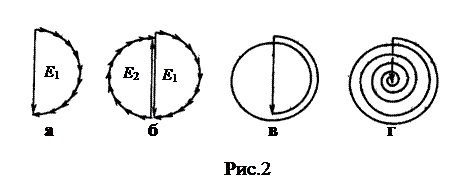 Расчет результирующей амплитуды колебаний от всех зон Френеля в точке А удобно производить на векторной диаграмме. Для этого мысленно разобьем каждую зону Френеля на большое число концентрических подзон одинаковой площади. Тогда амплитуду колебаний всей подзоны можно представить в виде суммы элементарных векторов, имеющих между собой малый сдвиг фаз, т. е. поворот на dj, а крайние элементарные векторы будут сдвинуты по фазе на угол p, т. е. направлены в противоположные стороны. Все элементарные векторы зоны вместе образуют полуокружность, а результирующая амплитуда колебаний Е1 от одной зоны может быть найдена суммированием всех векторов, т. е. образует вектор, соединяющий начало и конец цепочки элементарных векторов (рис.2,а).
Расчет результирующей амплитуды колебаний от всех зон Френеля в точке А удобно производить на векторной диаграмме. Для этого мысленно разобьем каждую зону Френеля на большое число концентрических подзон одинаковой площади. Тогда амплитуду колебаний всей подзоны можно представить в виде суммы элементарных векторов, имеющих между собой малый сдвиг фаз, т. е. поворот на dj, а крайние элементарные векторы будут сдвинуты по фазе на угол p, т. е. направлены в противоположные стороны. Все элементарные векторы зоны вместе образуют полуокружность, а результирующая амплитуда колебаний Е1 от одной зоны может быть найдена суммированием всех векторов, т. е. образует вектор, соединяющий начало и конец цепочки элементарных векторов (рис.2,а).
Аналогично можно сделать построение, включая вторую зону (рис.2,б). Результирующий вектор Е2 направлен против Е1 и по абсолютной величине несколько меньше Е1. Последнее обстоятельство связано с тем, что, хотя площади зон одинаковы, но вторая зона слегка наклонена по отношению к наблюдателю в точке А. Однако суммарная амплитуда колебаний Е1 + Е2 мала (рис.2,б).
 Графически расчет амплитуды колебаний можно производить, заменяя цепочки векторов соответствующими частями окружности. На рис.2 (в и г) приведены такие построения для трех и большего числа зон сферического волнового фронта. Сравнивая случаи а и г, заметим, что амплитуда колебаний от 1-ой зоны Френеля в два раза (а интенсивность света I в 4 раза, так как I » A2) больше, чем соответствующая амплитуда от бесконечного числа зон.
Графически расчет амплитуды колебаний можно производить, заменяя цепочки векторов соответствующими частями окружности. На рис.2 (в и г) приведены такие построения для трех и большего числа зон сферического волнового фронта. Сравнивая случаи а и г, заметим, что амплитуда колебаний от 1-ой зоны Френеля в два раза (а интенсивность света I в 4 раза, так как I » A2) больше, чем соответствующая амплитуда от бесконечного числа зон.
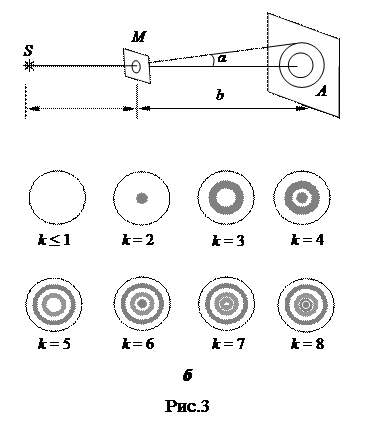
Пусть имеется точечный источник S и непрозрачная пластинка M с круглым отверстием (рис.3,а). Требуется определить освещенность в точке А, лежащей на прямой, проходящей от источника S через центр отверстия. Очевидно, отверстие пропустит лишь часть сферической волны. Освещенность в точке А будет определяться действием только этой части фронта, т. е. только открытыми зонами Френеля, число которых зависит от диаметра отверстия, длины волны и геометрии опыта.
Если число открытых зон К четное, то графический расчет интенсивности (рис.2,б) приводит к исчезающе малой интенсивности, т. е. в точке А будет темнота, а при нечетном К (рис.2,а, в) в точке А будет максимальная освещенность.
Очевидно, она должна быть симметричной относительно точки А (так как в точках, находящихся на одном и том же расстоянии от центральной, условия дифракции будут одинаковы). При этом, если в точке на оси мы наблюдаем светлое пятно, то вокруг него мы обнаружим темное кольцо, вокруг которого заметим светлое кольцо, т. е. картина дифракции представляет собой чередующиеся темные и светлые кольца (окружности) (рис.3,б).
Угол a, характеризующий направление на какой-либо дифракционный максимум, называется углом дифракции (рис.3,а). Можно (хотя и непросто) показать, что направление на первое кольцо характеризуется углом 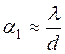 (точнее 1,22
(точнее 1,22 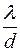 ), где d – диаметр отверстия.
), где d – диаметр отверстия.
