Естественный и поляризованный свет

Поляризация света

5.1 Поляризация электромагнитных волн

При изучении явлений интерференции и дифракции вопрос о том, являются ли волны продольными или поперечными имел второстепенное значение. Если задано направление распространения электромагнитной волны, а также одного из ее векторов, например 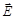, то направление другого определяется однозначно. Однако, таких взаимно перпендикулярных направлений в плоскости, нормальной к направлению распространения света, бесконечное множество. Поэтому, при рассмотрении электромагнитных волн отдельно выделяют вопрос об ориентации в пространстве векторов 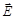и или поляризации волн. Волна называется линейно- или плоско поляризованной, если 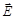все время лежит в одной плоскости, не меняющей своей ориентации в пространстве, в которой также расположен вектор . Эту плоскость будем называть плоскостью поляризации.

Рассмотрим суперпозицию двух линейно поляризованных волн с одной и той же частотой и одинаковым вектором . Для определенности будем считать, что параллелен оси Oz, а световые вектора перпендикулярны друг другу, т.е. вектор 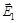колеблется в плоскости xOz, а – в плоскости yOz. Тогда,

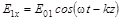; . (5.1.1)

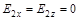; . (5.1.2)

Здесь d – сдвиг фаз между колебаниями. Напряженность результирующего вектора с течением времени будет меняться непрерывно. Так как начала векторов 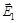и лежат на оси Oz, то начало результирующего вектора 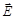также лежит на ней. Координата конца вектора 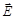меняется с течением времени, причем 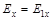, 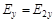. Для нахождения уравнения кривой, вдоль которой движется конец вектора 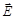, распишем косинус суммы в уравнении (5.1.2), а уравнение (5.1.1) оставим без изменения

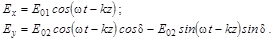
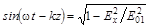Из формулы (5.1.1) следует, что , а следовательно . Тогда,

.

Перенесем первое слагаемое из правой части равенства в левую, и, возведем обе части уравнения в квадрат

.

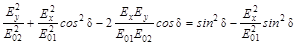Перенеся второе слагаемое из правой части равенства в левую, и учитывая, что cos² d + sin² d = 1, получим

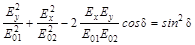. (5.1.3)

Рассмотрим различные частные случаи, описываемые этим уравнением.

1.

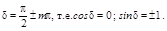
Тогда, (5.1.3) принимает вид

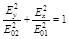. (5.1.4)

Это уравнение эллипса с центром в начале координат. Полуоси эллипса направлены вдоль осей координат и равны 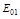и . Выясним направление вращения вектора . При 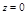уравнение (5.1.2) имеет вид

;

.

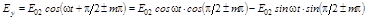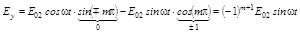Тогда

Следовательно, конец вектора вращается по часовой стрелке, если m четное и против часовой, если m нечетное. Наблюдение ведется со стороны, в которую движется волна. Такую волну называют эллиптически поляризованной. Если 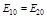, то эллипс вырождается в окружность. В этом случае говорят о круговой поляризации электромагнитных волн.

2.

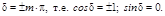
В этом случае уравнение (5.1.3) примет вид:

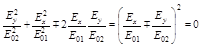или .

Приведем это выражение к более привычному виду

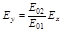(рис. а); 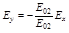(рис. б). (5.1.5)

Уравнения (5.1.5) являются уравнениями прямых, проходящих через начало координат и лежащих в первой и третьей (рис. а) или второй и четвертой (рис. б) четвертях соответственно. Конец вектора принимает всевозможные значения, лежащие на отрезке АБ или А'Б', то есть поляризация такой волны тоже линейная.

В произвольном случае выражение (5.1.3) также описывает эллипс, главные оси которого не совпадают с осями координат. Этот эллипс вписан в прямоугольник со сторонами с центром в начале координат.

Все изложенное выше показывает, что любая поляризованная волна может быть представлена в виде суперпозиции двух линейно поляризованных волн.

Естественный и поляризованный свет

Очевидно, что отдельный волновой цуг является линейно поляризованной волной. Однако, так как реальные источники света излучают множество независимых друг от друга цугов, то в каждый момент времени 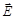, , 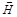хоть и остаются взаимно перпендикулярными, но направления 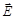и 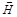беспорядочно меняются с течением времени. Такой свет называют естественным или неполяризованным. Поляризованный свет получают при пропускании естественного света через специальные устройства, называемые поляризаторами или поляроидами. Поляризаторы можно применять и для исследования поляризации света. В этом случае их называют анализаторами. Действие поляризаторов чаще всего основано на том, что материал, из которого сделан прибор, сильно поглощает световые лучи, в которых вектор 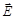перпендикулярен определенному направлению, называемому оптической осью. Если же вектор 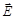параллелен оптической оси, то такие лучи проходят через поляризатор почти без поглощения.

Так как направления светового вектора в естественном свете равновероятны, то поляризатор поглотит, в среднем, половину энергии светового потока. Следовательно, интенсивность плоско поляризованного светового пучка вдвое меньше интенсивности естественного, из которого он был получен.

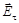Если свет проходит через два поляризатора, поставленных друг к другу так, что их оси образуют между собой некоторый угол a, то интенсивность результирующего пучка еще более уменьшится. Пусть первый поляроид пропустит свет, вектор которого параллелен его оси OA. Обозначим через I₀ интенсивность этого света. Разложим на и 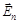. Составляющая 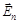будет задержана вторым поляроидом. Через оба поляроида пройдет свет, для которого 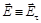, длина которого равна 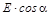. Интенсивность света, прошедшего через оба поляроида, определяется соотношением

, (5.2.1)

называемым законом Малюса.

Величину, характеризующую поляризованность света, называют степенью поляризации. Она определяется по формуле

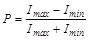, (5.2.2)

где 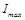и – максимальная и минимальная интенсивности света, соответствующие двум взаимно перпендикулярным направлениям вектора 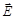. Для естественного света 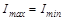, то есть степень поляризации такой волны равна нулю. Для плоско поляризованного света минимальное значение интенсивности 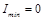, следовательно, ее степень поляризации равна единице. Поляризация эллиптически поляризованного света зависит от соотношения длин полуосей эллипса.