Расчетно-графическая работа №7. Расчёт продольных сил и нормальных напряжений

Задание 1.Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса. Двухступенчатый стальной брус нагружен силами F₁, F₂; F₃. Площади поперечных сечений А₁ и А₂.

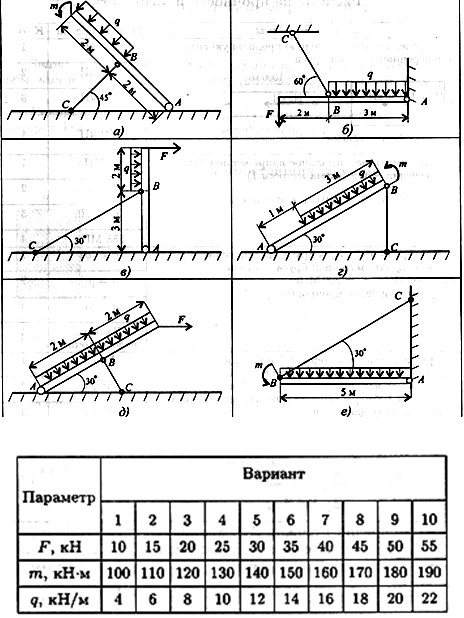
Задание 2.Балка АВ, на которую действуют указанные на­грузки, удерживается в равновесии тягой ВС. Определить разме­ры поперечного сечения тяги для двух случаев: 1) сечение — круг; 2) сечение — уголок равнополочный по ГОСТ 8509-86. Принять [σ] = 160 МПа. Собственный вес конструкции не учитывать.

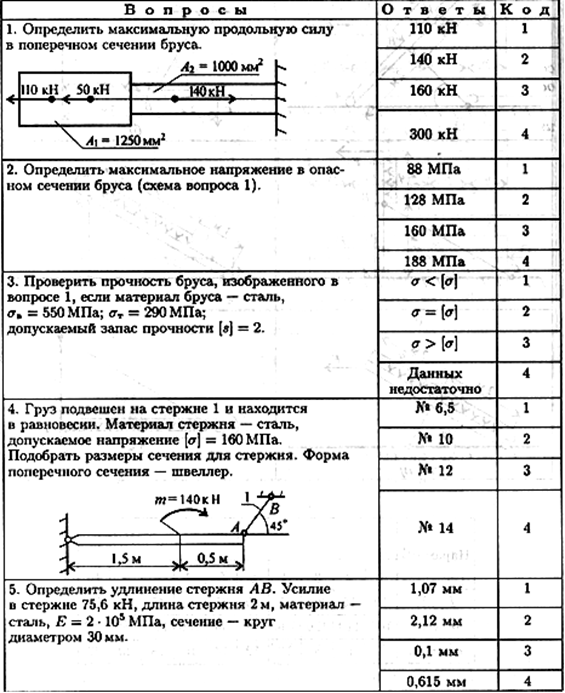
При защите работы ответить на вопросы тестового задания.

Тема 2.2. Растяжение и сжатие. Расчеты на прочность и жесткость.

ЛЕКЦИЯ 23

Тема 2.3. Практические расчеты на срез и смятие. Основные предпосылку расчетов и расчетные формулы

Иметь представление об основных предпосылках и условностях расчетов о деталях, работающих на срез и смятие.

Знать внутренние силовые факторы, напряжения и деформа­ции при сдвиге и смятии, условия прочности.

Уметь определять площади среза и смятия.

Детали соединений (болты, штифты, шпонки, заклепки) рабо­тают так, что можно учитывать только один внутренний силовой фактор — поперечную силу. Такие детали рассчитываются на сдвиг.

Сдвиг (срез)

Сдвигом называется нагружение, при котором в поперечном се­чении бруса возникает только один внутренний силовой фактор — поперечная сила.

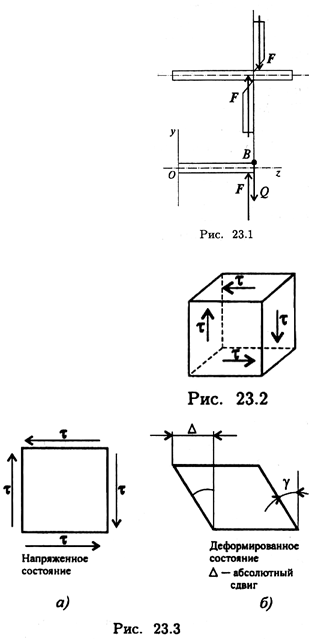
Рассмотрим брус, на который действу­ют равные по величине, противоположно направленные, перпендикулярные продоль­ной оси силы (рис. 23.1).

Применим метод сечений и определим внутренние силы упругости из условия равновесия каждой из частей бруса:

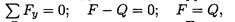
где Q — поперечная сила. Естественно считать, что она вызовет появление только касательных напряжений τ.

Рассмотрим напряженное состояние в точке В поперечного сечения.

Выделим элемент в виде бесконечно малого параллелепипеда, к граням которо­го приложены напряжения (рис. 23.2).

Исходя из условия равновесия точки В, внутри бруса при возникновении касательного напряжения τ на правой вертикальной площадке такое же напря­жение должно возникнуть и на левой площадке. Они образуют пару сил. На горизонтальных площадках возникнут такие же напряжения, образующие такую же пару обратного направления (рис. 23.3).

Такое напряженное состояние называется чистым сдвигом. Здесь действует закон парности касательных напряжений:

При сдвиге в окрест­ностях точки на взаимно перпендикулярных площад­ках возникают равные по величине касательные на­пряжения, направленные на соседних площадках ли­бо от ребра, либо к ребру (рис. 23.3а).

В результате площадки сдвигаются на угол γ, назы­ваемый углом сдвига.

При сдвиге выполняется закон Гука, который в данном случае записывается следующим образом:

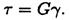
Здесь τ — напряжение; G — модуль упругости сдвига; γ — угол сдвига.

При отсутствии специальных испытаний G можно рассчитать по формуле

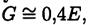
Е — модуль упругости при растяжении.

[G] = МПа.

Расчет деталей на сдвиг носит условный характер.

Для упрощения расчетов принимается ряд допущений:

— при расчете на сдвиг изгиб деталей не учитывается, хотя силы, действующие на деталь, образуют пару;

— при расчете считаем, что силы упругости распределены по сечению равномерно;

— если для передачи нагрузки используют несколько деталей, считаем, что внешняя сила распределяется между ними равномерно.

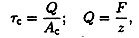Откуда формула для расчета напряжений имеет вид:

где τ_с — касательное напряжение; Q — поперечная сила; Ас — площадь сдвига; F — внешняя сдвигающая сила; z — количество деталей.

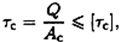Условие прочности при сдвиге (срезе)

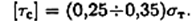[τ_с] — допускаемое напряжение сдвига, обычно его определяют по формуле

При разрушении деталь перерезается поперек. Разрушение детали под действием поперечной силы называют срезом.

Смятие

Довольно часто одновременно со сдвигом происходит смятие боковой поверхности в месте контакта в результате передачи нагрузки от одной поверхности к другой. При этом на поверхности возникают сжимающие напряжения, называемые напряжениями смятия, σ_см.

Расчет также носит условный характер. Допущения подобны принятым при расчете на сдвиг (см. выше), однако при расчете боковой цилиндрической поверхности напряжения по поверхности распределены не равномерно, поэтому расчет проводят для наиболее нагруженной точки (на рис. 23.4 б). Для этого вместо боковой поверхности цилиндра в расчете используют плоскую поверхность, проходящую через диаметр. На рис. 23.4 показана примерная схема передачи давления на стержень заклепки.

Таким образом, условие прочности при смятии можно выразить соотношением

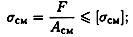
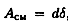
где d — диаметр окружности сечения; δ — наименьшая высота соединяемых пластин; Асм — расчетная площадь смятия; F — сила взаимодействия между деталями, допускаемое напряжение смятия: