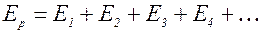Принцип Гюйгенса Френеля
Дифракция света
Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики.
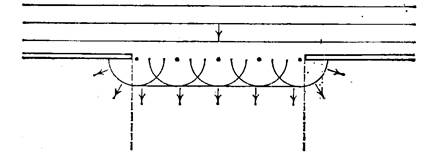 Рис.8.1 Рис.8.1 |
Пусть на плоскую преграду с отверстием падает параллельный ей фронт волны (рис. 8.1). По Гюйгенсу каждая точка выделяемого отверстием участка волнового фронта служит центром вторичных волн, которые в однородной и изотропной среде будут сферическими. Построив огибающую вторичных волн, мы убеждаемся в том, что за отверстием волна проникает в область геометрической тени (на рисунке границы этой области показаны пунктиром),т.е огибает края преграды.
. Благодаря дифракции света возникают волны (рис. 8.2), отражённые от освещаемых объектов, и становится возможным их визуализация (" видение ").
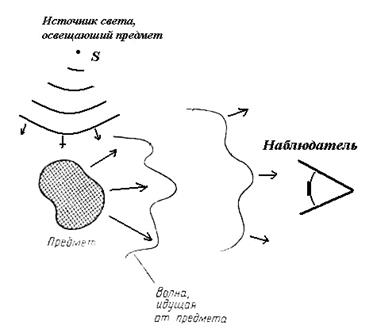 Рис.8.2 Рис.8.2 |
Дифракция световых волн определяет качество оптических приборов, в частности их разрешающую способность.
Огибание препятствий звуковыми волнами (т. е. дифракция звуковых волн) наблюдается постоянно в обыденной жизни. Для наблюдения дифракции световых волн необходимо создание специальных условий. Это обусловлено малостью длин световых волн. Мы знаем, что в пределе при l→ 0 законы волновой оптики переходят в законы геометрической оптики. Следовательно, отклонения от законов геометрической оптики при прочих равных условиях оказываются тем меньше, чем меньше длина волны.
Принцип Гюйгенса Френеля.
Проникновение световых волн в область геометрической тени может быть объяснено с помощью принципа Гюйгенса. Однако этот принцип не дает сведений об амплитуде, а следовательно и об интенсивности волн, распространяющихся в различных направлениях. Френель дополнил принцип Гюйгенса представлением об интерференции вторичных волн, т.е по Френелю все вторичные источники когерентны между собой. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны
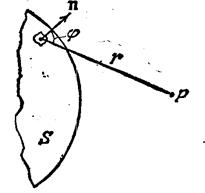 Рис.8.3 Рис.8.3 |
в любой точке пространства. Развитый таким способом принцип Гюйгенса получил название принципа Гюйгенса — Френеля.
Согласно принципу Гюйгенса — Френеля каждый элемент волновой поверхности S (рис8.3) служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS. Амплитуда сферической волны убывает с расстоянием г от источника по закону 1/г (Следовательно, от каждого участка dS волновой поверхности в точку Р, лежащую перед этой поверхностью, приходит колебание
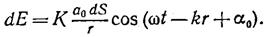 (8.1)
(8.1)
В этом выражении 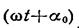 — фаза колебания в месте расположения волновой поверхности S, k — волновое число, г — расстояние от элемента поверхности dS до точки Р. Множитель
— фаза колебания в месте расположения волновой поверхности S, k — волновое число, г — расстояние от элемента поверхности dS до точки Р. Множитель 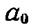 определяется амплитудой светового колебания в том месте, где находится dS. Коэффициент К зависит от угла j между нормалью n к площадке dS и направлением от dS к точке Р. При j =0 этот коэффициент максимален, при j =p/2 он обращается в нуль.
определяется амплитудой светового колебания в том месте, где находится dS. Коэффициент К зависит от угла j между нормалью n к площадке dS и направлением от dS к точке Р. При j =0 этот коэффициент максимален, при j =p/2 он обращается в нуль.
Результирующее колебание в точке Р представляет собой суперпозицию колебаний, взятых для всей волновой поверхности S:
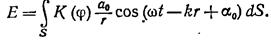 (8,2)
(8,2)
Эта формула является аналитическим выражением принципа Гюйгенса — Френеля.
Сказанное означает, что при вычислении амплитуды колебания, порождаемого в точке Р световой волной, распространяющейся от реального источника, можно заменять этот источник совокупностью вторичных источников, расположенных вдоль волновой поверхности. А в этом и состоит суть принципа Гюйгенса — Френеля.
Так как вторичные источники когерентны между собой, то дифракционная картина будет представлять собой перераспределение интенсивности светового потока. Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. По историческим причинам перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией волн. Перераспределение интенсивности, возникающее вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией волн. Наблюдение дифракции осуществляется обычно по следующей схеме. На пути световой волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности световой волны. За преградой располагается экран, на котором возникает дифракционная картина.
Различают два вида явления дифракции в зависимости от расстояния точки наблюдения до препятствия или неоднородности, а также от вида волнового фронта в точке наблюдения. Если точка наблюдения расположена достаточно далеко от препятствия и в точку наблюдения после взаимодействия с неоднородностью приходит плоская волна, то говорят о дифракции Фраунгофера. В остальных случаях говорят о дифракции Френеля.
В качестве примера рассмотрим взаимодействие светового потока от источника 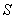 с непрозрачной плоской преградой, в которой прорезано отверстие произвольной формы. При дифракции Френеля (рис. 8.4а) в точку наблюдения
с непрозрачной плоской преградой, в которой прорезано отверстие произвольной формы. При дифракции Френеля (рис. 8.4а) в точку наблюдения 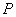 , расположенную на экране на конечном расстоянии
, расположенную на экране на конечном расстоянии 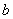 от преграды, приходят сферические волны от источника, расположенного на конечном расстоянии
от преграды, приходят сферические волны от источника, расположенного на конечном расстоянии 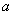 от преграды, и от точек контура, ограничивающего отверстие. При дифракции Фраунгофера (рис. 8.4b) световой волны от источника
от преграды, и от точек контура, ограничивающего отверстие. При дифракции Фраунгофера (рис. 8.4b) световой волны от источника 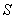 , бесконечно удалённого от преграды, в точку наблюдения
, бесконечно удалённого от преграды, в точку наблюдения 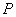 , также бесконечно удалённую от преграды, приходят плоские волны.
, также бесконечно удалённую от преграды, приходят плоские волны.
 Рис.8.4 Рис.8.4 |
Отсюда следует, что дифракция Френеля проявляется в виде интерференции сферических (цилиндрических) волн, приходящих в точку наблюдения от неоднородности, с которой взаимодействует электромагнитная волна (свет). Интерференция цилиндрических волн, представляющая собой частный случай интерференции сферических волн, имеет место в том случае, когда и световая волна и неоднородность среды распространения обладают общей осью симметрии, вследствие которой поле волны и параметры неоднородности одинаковы в любом сечении, перпендикулярном оси симметрии.
Дифракция Фраунгофера обусловлена интерференцией параллельных, плоских волн (лучей), приходящих в точку наблюдения от неоднородности, с которой взаимодействует электромагнитная волна (свет). С помощью линзы 2 (рис. 8.5)
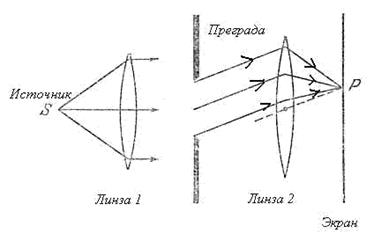 Рис.8.5 Рис.8.5 |
дифракцию Фраунгофера можно наблюдать на экране, расположенном на конечном расстоянии от преграды, с которой взаимодействует свет (электромагнитная волна). Линза 1 (рис. 8.6), в фокусе которой расположен источник 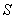 , используется для освещения отверстия в преграде плоской волной.
, используется для освещения отверстия в преграде плоской волной.
Зоны Френеля
Как следует из принципа Гюйгенса- Френеля амплитуда волны в точке наблюдения 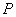 (рис. 8.3), создаваемая источником монохроматической электромагнитной волны в точке
(рис. 8.3), создаваемая источником монохроматической электромагнитной волны в точке 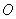 , может быть найдена как суперпозиция амплитуд сферических волн, испускаемых вторичными источниками на произвольной замкнутой поверхности
, может быть найдена как суперпозиция амплитуд сферических волн, испускаемых вторичными источниками на произвольной замкнутой поверхности 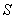 , охватывающей точку
, охватывающей точку 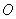 в соответствии с выражением (8.2).
в соответствии с выражением (8.2).
Вычисления по формуле (8.2) представляют собой в общем случае очень трудную задачу. Однако, как показал Френель, в случаях, отличающихся симметрией, нахождение амплитуды результирующего колебания может быть осуществлено простым алгебраическим или геометрическим суммированием.
Чтобы понять суть метода, разработанного Френелем, амплитуду светового колебания, возбуждаемого в точке Р сферической волной, распространяющейся в изотропной, однородной среде из точечного источника S (рис. 8.6). Волновые поверхности такой световой волны симметричны относительно прямой линии SP. Воспользовавшись этим, разобьем изображенную на рисунке волновую поверхность на кольцевые зоны, построенные так, что расстояния от краев каждой, зоны до точки Р отличаются на l/2. Обладающие таким свойством зоны носят название зон Френеля.
 Рис.8.6 Рис.8.6 |
Из рис. 8.6 видно, что расстояние bm от внешнего края m-й равно
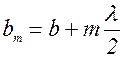 (8.3)
(8.3)
(b — расстояние от вершины волновой поверхности О до точки Р). Колебания, приходящие в точку Р от аналогичных точек двух соседних зон (т. е. от точек, лежащих в середине зон, или у внешних краев зон и т. д.), находятся в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на p.
Вычислим радиус зон Френеля. Так, граница  - ой зоны Френеля (
- ой зоны Френеля ( 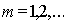 ) отстоит от прямой
) отстоит от прямой 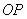 (рис. 8.6) на расстоянии
(рис. 8.6) на расстоянии 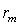 , называемом радиусом
, называемом радиусом 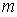 - ой зоны Френеля. Найдём радиус
- ой зоны Френеля. Найдём радиус 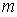 - ой зоны Френеля. Как следует из геометрических соображений (рис. 8.7):
- ой зоны Френеля. Как следует из геометрических соображений (рис. 8.7):
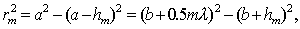 (8.4)
(8.4)
где 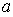 - расстояние вдоль прямой
- расстояние вдоль прямой 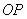 от источника до центра волнового фронта ;
от источника до центра волнового фронта ; 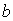 - расстояние вдоль прямой
- расстояние вдоль прямой 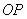 от центра волнового фронта до точки наблюдения.
от центра волнового фронта до точки наблюдения.
Из 8.4, пренебрегая 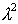 , для не очень больших
, для не очень больших 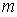 найдём
найдём 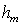 :
:
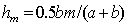 (8.5)
(8.5)
С помощью этого соотношения из (8.4) найдём
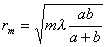 (8.6)
(8.6)
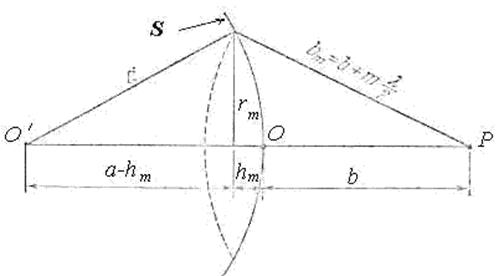 Рис8.7 Рис8.7 |
В частном случае бесконечно удалённого источника от точки наблюдения ( 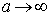 ) волновой фронт
) волновой фронт  является плоскостью и радиус m-ой зоны Френеля определяется формулой
является плоскостью и радиус m-ой зоны Френеля определяется формулой
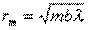 (8.7)
(8.7)
Принимая во внимание (рис. 8.5), находим площадь 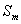 сферического сегмента радиуса
сферического сегмента радиуса 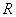 и высоты
и высоты 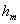
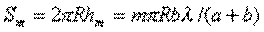 (8.8)
(8.8)
и получаем, что площадь 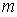 - ой зоны Френеля
- ой зоны Френеля 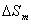 :
:
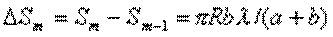 (8.9)
(8.9)
не зависит от 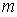 .Это значит, что в каждой зоне Френеля находится одинаковое число вторичных источников, а, следовательно, суммарную амплитуду вторичных источников можно заменить амплитудой зоны Френеля.
.Это значит, что в каждой зоне Френеля находится одинаковое число вторичных источников, а, следовательно, суммарную амплитуду вторичных источников можно заменить амплитудой зоны Френеля.
Итак, площади зон Френеля примерно одинаковы. Расстояние bm от зоны до точки Р медленно растет с номером зоны m Угол j между нормалью к элементам зоны и направлением на точку Р также растет с m. Все это приводит к тому, что амплитуда Em колебания, возбуждаемого m-й зоной в точке Р, монотонно убывает с ростом m. Таким образом, амплитуды колебаний, возбуждаемых в точке Р зонами Френеля, образуют монотонно убывающую последовательность:
E1>E2>E3> Em >Em+n
Фазы колебаний, возбуждаемых соседними зонами, отличаются на p.
Действительно, пусть 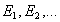 - амплитуды, создаваемые первой, второй и т.д. зонами Френеля. Тогда искомая амплитуда в точке
- амплитуды, создаваемые первой, второй и т.д. зонами Френеля. Тогда искомая амплитуда в точке 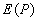 , создаваемая всеми зонами Френеля в точке наблюдения, равна
, создаваемая всеми зонами Френеля в точке наблюдения, равна
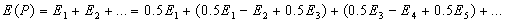 (8.10)
(8.10)
Как было отмечено выше, можно считать, что вклады от соседних зон примерно равны и их величины монотонно уменьшаются. По этой причине можно считать выражения в скобках в (8/10) равными нулю, т. е. имеет место равенство для любого m .>1
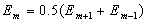 .
.
Тогда из выражения (8.10) получим:
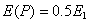 (8.11)
(8.11)
Итак, амплитуда результирующего колебания, получающегося вследствие взаимной интерференции света, идущего в точку Р от различных участков сферической волны, меньше амплитуды первой зоны Френеля. Так, как в однородной изотропной среде интенсивность распространяющегося света определяется только амплитудой первой зоны Френеля, то можно оценить радиус того цилиндрического канала, по которому распространяется свет: пусть а=b=1м, l=0,5мкм, тогда r1=0,5мм. Следовательно, распространение света от точки S к точке P происходит в узком канале, т.е. прямолинейно, что соответствует законам геометрической оптики. Таким, образом, теория зон Френеля не противоречит законам геометрической оптики.
Учитывая, что интенсивность волны пропорциональна квадрату модуля электромагнитных векторов, можно заключить, что интенсивность поля 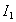 , создаваемого первой зоной Френеля, в четыре раза больше интенсивности волны источника
, создаваемого первой зоной Френеля, в четыре раза больше интенсивности волны источника 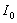 в точке наблюдения, создаваемой всеми вторичными источниками на поверхности
в точке наблюдения, создаваемой всеми вторичными источниками на поверхности 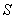 :
:
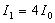 (8.12)
(8.12)
Зонные пластинки.
Мы нашли выражение для радиусов зон Френеля сферических световых волн
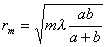 (8.13)
(8.13)
Используя, это выражение , можно приготовить экран, состоящий из последовательно чередующихся прозрачных и непрозрачных колец, радиусы которых удовлетворяют условию 8.13 для заданных значений a, b и l. Приготовленная таким образом пластинки носит название амплитудной зонной пластинки. Колебания от четных и нечетных зон Френеля находятся в противофазе и, следовательно, взаимно ослабляют друг друга. Если поставить на пути световой волны приготовленную пластинку, которая перекрывала бы все четные или нечетные зоны, то интенсивность света в точке Р резко возрастает. Такая пластинка действует подобно собирающей линзе.
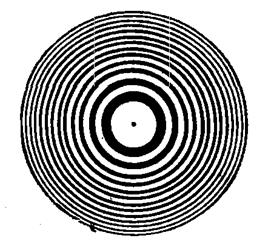 Рис.8.8 Рис.8.8 |
На рис. 8.8 изображена пластинка, перекрывающая четные зоны.
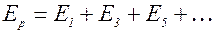 Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на p. Это можно осуществить о помощью
Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на p. Это можно осуществить о помощью
прозрачной пластинки, толщина которой в местах, соответствующих четным или нечетным зонам, отличается на надлежащим образом подобранную величину. Такая пластинка называется фазовой зонной пластинкой. По сравнению с перекрывающей зоны амплитудной зонной пластинкой, фазовая дает дополнительное увеличение амплитуды в два раза, а интенсивности света — в четыре раза.
Для фазовой пластинки результирующую амплитуду светового вектора можно записать следующим образом: