Нормальное напряжение характеризует сопротивление сечения растяжению или сжатию

Касательное напряжение характеризует сопротивление сечения сдвигу.

Сила N (продольная) вызывает появление нормального напря­жения σ. Силы Q_x и Q_y вызывают появление касательных напря­жений τ. Моменты изгибающие М_х и М_у вызывают появление нор­мальных напряжений σ, переменных по сечению.

Крутящий момент М_Z вызывает сдвиг сечения вокруг продоль­ной оси, поэтому появляются касательные напряжения τ.

Примеры решения задач

Последовательность построения эпюр продольных сил

1. Изобразить расчетную схему бруса и приложить заданные силы. При необ­ходимости определить опор­ную реакцию из уравнения равновесия.
2. Брус разбить на участ­ки соответственно точкам приложения сил.
3. Определить по методу сечений продольную силу для каждого участка.
4. Найденные величины продольных сил отложить в масштабе в виде ординат, перпендикулярных оси стерж­ня. Через концы ординат провести линии; проставить знаки и заштриховать эпю­ру параллельно ординатам

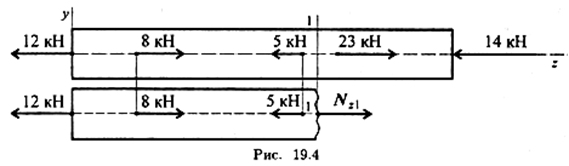
Пример 1. Определить величину продольной силы в сечении 1-1 (рис. 19.4).

Решение

Используем уравнение равновесия

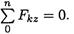
Рассматривая левую часть бруса, определяем

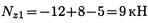
Рассматривая правую часть бруса, определяем N_z1 = 23 — 14 = 9кН.

Величина продольной силы в сечении не зависит от того, какая часть бруса рассматривается.

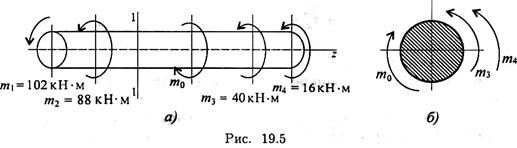
Пример 2. Определить внутренний силовой фактор в сечении 1-1 (рис. 19.5а).

Решение

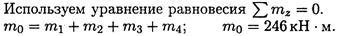
Рассматриваем правую часть бруса. На отсеченную часть бруса принято смотреть со стороны отброшенной части (рис. 19.5, б). Полу­чаем M_z = 246 – 40 – 16 = 190 кН • м.

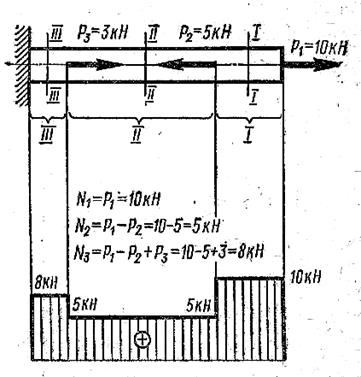
Пример 3. Для бруса, изображенного на рис. 2.4, а, построить эпюру продольных сил.

Решение

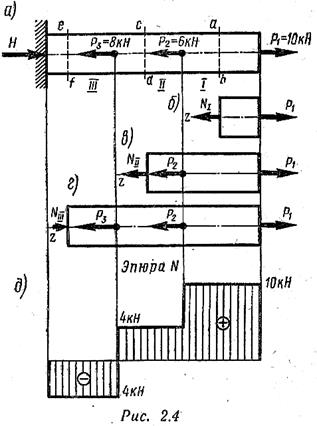
Заданный брус имеет три участка 1, II, III (рис. 2.4, а). Границами участков при построении эпюры N являются сечения, в которых приложены внешние силы.

1. Проведем произвольное сечение аb на участке 1 и, отбросив левую часть бруса, рассмотрим равновесие пра­вой части, изображенной отдельно на рис. 2.4, б.

2. На оставленную часть действуют сила Р₁ и искомое усилие N₁. Проектируя на ось z силы, действующие на оставленную часть, получаем:

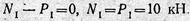
Значение получилось со знаком плюс, что указы­вает на совпадение ее предположительного (см. рис. 2.4, 6) направления с действительным. Сила направлена от сечения, т. е. участок I испытывает растяжение.

3. Проведем произвольное сечение cd на участке II, от­бросим левую часть бруса и рассмотрим равновесие оставленной (правой) части, изображенной отдельно на рис. 2.4, в. На оставленную часть действуют силы Р₁, Р₂ и искомое усилие N_II.. Проектируя эти силы на ось г, получаем

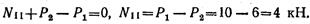
Сила N_II направлена от сечения, т. е. участок II испытывает растяжение.

4.

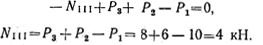Проведем произвольное сечение еf на участке III, от­бросим левую часть бруса и рассмотрим равновесие оставлен­ной (правой) части, изображенной отдель­но на рис. 2.4, г. На оставленную часть действуют силы Р₁, Р₂, Р₃ и искомое уси­лие N_III. Проекти­руя эти силы на ось z, получаем

Сила N_III направ­лена к сечению, т. е. участок III испыты­вает сжатие.

Напомним, что продольные силы, соответствующие растяжению, принято считать положительными, а соот­ветствующие сжатию — отрицательными.

Эпюра продольных сил показана на рис. 2.4, д.

Контрольные вопросы и задания

1. Какие силы в сопротивлении материалов считают внешними? Какие силы являются внутренними?

2. Какими методами определяют внешние силы? Как называют метод для определения внутренних сил?

3. Сформулируйте метод сечений.

4. Как в сопротивлении материалов располагают систему коор­динат?

5. Что в сопротивлении материалов называют внутренними си­ловыми факторами? Сколько в общем случае может возникнуть внутренних силовых факторов?

6. Запишите систему уравнений, используемую при определении внутренних силовых факторов в сечении?

7. Как обозначается и как определяется продольная сила в се­чении?

8. Как обозначаются и как определяются поперечные силы?

9. Как обозначаются и определяются изгибающие и крутящий моменты?

10. Какие деформации вызываются каждым из внутренних си­ловых факторов?

11. Что называют механическим напряжением?

12. Как по отношению к площадке направлены нормальное и касательные напряжения? Как они обозначаются?

13. Какие напряжения возникают в поперечном сечении при дей­ствии продольных сил?

14. Какие напряжения возникают при действии поперечных сил?

15.

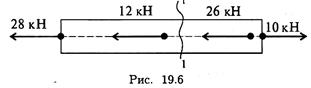С помощью метода сечений определите величину внутренне­го силового фактора в сечении 1-1 и вид нагружения (рис. 19.6).

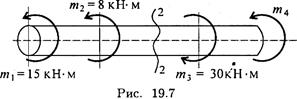
16. С помощью метода сечений определите величину момента m₄, величину внутреннего силового фактора в сечении 2-2 и вид нагружения (рис. 19.7).

17. Ответьте на вопросы тестового задания.

Тема 2.1. Основные положения, метод сечений, напряжения