Порядок выполнения расчета на устойчивость

1. Получение сведений о материале стержня для определения предельной гибкости стержня расчетным путем или по таблице:

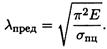
2. Получение сведений о геометрических размерах поперечно­го сечения, длине и способах закрепления концов для определения категории стержня в зависимости от гибкости:

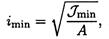
где А — площадь сечения; J_min— минимальный момент инерции (из осевых);

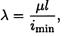
μ — коэффициент приведенной длины.

3. Выбор расчетных формул для определения критической силы и критического напряжения.

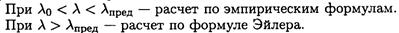
4. Проверка и обеспечение устойчивости.

При расчете по формуле Эйлера условие устойчивости:

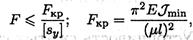
F — действующая сжимающая сила; [s_у] — допускаемый коэффици­ент запаса устойчивости.

При расчете по формуле Ясинского

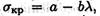
где a, b — расчетные коэффициенты, зависящие от материала (величины ко­эффициентов приводятся в таблице 36.1)

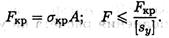
В случае невыполнения условий устойчивости необходимо уве­личить площадь поперечного сечения.

Иногда необходимо определить запас устойчивости при задан­ном нагружении:

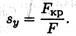
При проверке устойчивости сравнивают расчетный запас вынос­ливости с допускаемым:

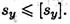
Примеры решения задач

Пример 1. Рассчитать гибкость стержня. Круглый стержень диаметром 20 мм закреплен так, как показано на рис. 37.1.

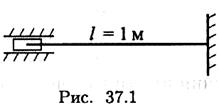Решение

1. Гибкость стержня определяется по формуле

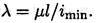
2. Определяем минимальный радиус инерции для круга.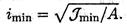

Подставив выражения для J_min и А (сечение круг)

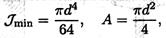
получим

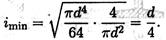
1. Коэффициент приведения длины для данной схемы крепле­ния μ= 0,5.
2. Гибкость стержня будет равна

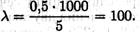
Пример 2. Как изменится критическая сила для стержня, ес­ли изменить способ закрепления концов? Сравнить представленные схемы (рис. 37.2)

Решение

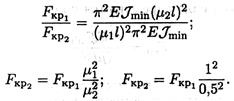
Критическая сила увеличится в 4 раза.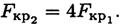

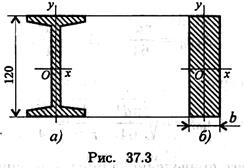Пример 3. Как изменится критическая сила при расчете на устойчивость, если стержень двутаврового сечения (рис. 37.3а, дву­тавр № 12) заменить стержнем прямоугольного сечения той же пло­щади (рис. 37.3б)? Остальные параметры конструкции не меняются. Расчет выполнить по формуле Эйлера.

Решение

1. Определим ширину сечения прямоугольника, высота сечения равна высоте сечения двутавра. Геометрические параметры двутавра № 12 по ГОСТ 8239-89 следующие:

площадь сечения А₁ = 14,7см²;

минимальный из осевых моментов инерции .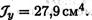

По условию площадь прямоугольного сечения равна площади сечения двутавра. Определяем ширину полосы при высоте 12 см.

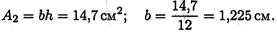
2. Определим минимальный из осевых моментов инерции.

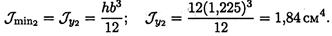
3. Критическая сила определяется по формуле Эйлера:

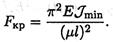
4. При прочих равных условиях отношение критических сил рав­но отношению минимальных моментов инерции:

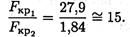
5. Таким образом, устойчивость стержня с сечением двутавр № 12 в 15 раз выше, чем устойчивость стержня выбранного пря­моугольного сечения.

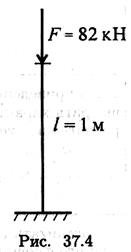Пример 4. Проверить устойчивость стержня. Стержень длиной 1 м защемлен одним концом, сечение — швеллер № 16, материал — СтЗ, запас устойчивости трехкратный. Стержень нагружен сжима­ющей силой 82 кН (рис. 37.4).

Решение

1. Определяем основные геометрические пара­метры сечения стержня по ГОСТ 8240-89. Швеллер № 16: площадь сечения 18,1см²; минимальный осевой момент сечения 63,3 см⁴; мини­мальный радиус инерции сечения г_т;_п = 1,87см.

2. Определяем категорию стержня в зависимости от гибкости.

Предельная гибкость для материала СтЗ λ_пред = 100.

Расчетная гибкость стержня при длине l = 1м = 1000мм

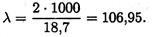
Рассчитываемый стержень — стержень большой гибкости, рас­чет ведем по формуле Эйлера.

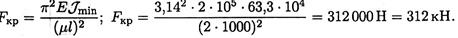
3. Допускаемая нагрузка на стержень

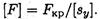
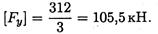
4. Условие устойчивости

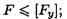
82кН < 105,5кН. Устойчивость стержня обеспечена.

Пример 5. На рис. 2.83 показана расчетная схема трубчатой стойки самолетной конструкции. Проверить стойку на устойчивость при [n_у] = 2,5, если она изготовлена из хромоникелевой стали, для которой Е = 2,1*10⁵ и σ_пц = 450 Н/мм².

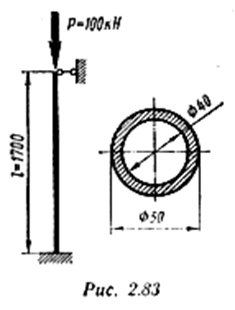Решение

Для расчёта на устойчивость должна быть известна критическая сила для заданной стойки. Необходимо установить, по какой формуле следует вычислять критическую силу, т. е. надо сопоставить гибкость стойки с предельной гибкостью для её материала.

Вычисляем величину предельной гибкости, так как табличных данных о λ,_пред для материала стойки не имеется:

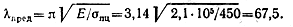
Для определения гибкости рассчитываемой стойки вычисляем геометрические характеристики ее поперечного сечения:

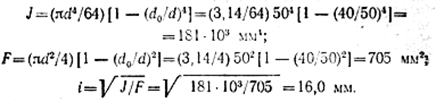
Определяем гибкость стойки:

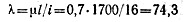
и убеждаемся, что λ < λ_пред, т. е. критическую силу можно опреде­лить ею формуле Эйлера:

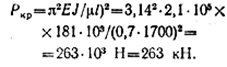
Вычисляем расчетный (действительный) коэффициент запаса устойчивости:

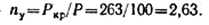
Таким образом, n_у > [n_у] на 5,2%.

Пример 2.87. Проверить на прочность и устойчи­вость заданную стержневую систему (рис. 2.86), Материал стержней — сталь Ст5 (σ_т = 280 Н/мм²). Требуемые коэффи­циенты запаса: прочности [n] = 1,8; устойчивости [n_у] = 2,2. Стержни имеют круглое поперечное сечение d₁ = d₂ = 20 мм, d₃ = 28 мм.

Решение

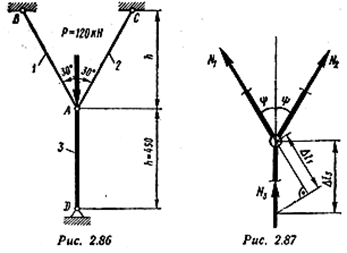
Вырезая узел, в котором сходятся стержни, и составляя уравнения равновесия для действующих на него сил (рис. 2.86)

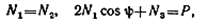
устанавливаем, что заданная система статически неопре­делима (три неизвестных усилия и два уравнения ста­тики). Ясно, что для расчета стержней на прочность и устойчивость необходимо знать величины продольных сил, возникающих в их поперечных сечениях, т. е. нужно раскрыть статическую неопределимость.

Составляем уравнение перемещений на основе диа­граммы перемещений (рис. 2.87):

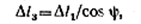
или, подставляя значения изменений длин стержней, по­лучаем

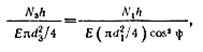
откуда

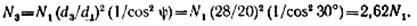
Решив это уравнение совместно с уравнениями ста­тики, найдем:

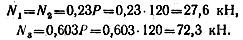
Напряжения в поперечных сечениях стержней 1 и 2 (см. рис. 2.86):

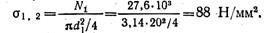
Их коэффициент запаса прочности

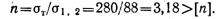
Для определения коэффициента запаса устойчивости стержня 3 надо вычислить критическую силу, а это тре­бует определения гибкости стержня, чтобы решить, какой формулой для нахождения N_Kp следует воспользоваться.

Итак, λ₀ < λ < λ_пред и крити­ческую силу следует определять по эмпирической формуле:

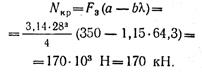
Коэффициент запаса устой­чивости

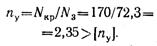
Таким образом, расчет пока­зывает, что коэффициент запаса устойчивости близок к требуемо­му, а коэффициент запаса проч­ности значительно выше требуемого, т. е. при увеличении нагрузки системы потеря устойчивости стержнем 3 вероят­нее, чем возникновение текучести в стержнях 1 и 2.