Частотные характеристики звена.

Колебательное звено.

Динамика процессов в колебательном звене описывается уравнением (1.16):

, (1.16)

где K- коэффициент усиления звена;

Т-постоянная времени колебательного звена, определяющая угловую
частоту свободных колебаний ;

- коэффициент демпфирования звена (или коэффициент затухания).

В зависимости от величины коэффициента демпфирования различают
четыре типа звеньев:

а) колебательное 0< <1;

б) апериодическое звено II порядка >1;

в) консервативное звено =0;

г) неустойчивое колебательное звено <0.

Общепринятая запись передаточной функции колебательного звена имеет вид (1.17):

. (1.17)

Переходная характеристика колебательного звена представлена на рис. 1.5:

Рис. 1.5

Весовая функция колебательного звена определяется по выражению

.

Частотные и временные характеристики звена имеют следующий вид:

-АФЧХ

;

-АЧХ

;

-ФЧХ

- ЛАЧХ

Графики частотных характеристик колебательного звена приведены на рисунке 1.6.

а – АФЧХ	б – АЧХ
в – ФЧХ	г – ЛАЧХ

Рис. 1.6.

Анализ АЧХ показывает, что для любого , если . При на графике появляется «горб», который уходит в бесконечность при .

Реальное интегрирующее звено.Реальное интегрирующее звено представляет собой последовательное соединение идеального интегрирующего звена и апериодического.

Динамика процесса в таком звене описывается следующим уравнением:

,

и передаточная функция примет вид

. (1.18)

Временные характеристики реального интегрирующего звена определяются по формулам:

Частотные характеристики реального интегрирующего звена определяются по формулам:

-АФЧХ

;

-АЧХ

;

-ФЧХ

- ЛАЧХ

Фоpсиpующеeзвeнопepвогопоpядка.

Дифференциальное уравнение и передаточная функция звена имеют вид

,

,

а частотные и временные характеристики определяются выражениями

, ,

, ,

, .

В системе MATLAB для описания моделей систем и действий над ними используется пакет прикладных программ ControlSystemToolbox [].

В пакете введен класс объектов, называемый lti–объекты –линейные с постоянными параметрами. При создании lti–объекта ему присваивается имя. Передаточная функция имеет две формы представления:

tf – форма, в которой передаточная функция задается двумя векторами–строками, составленными из коэффициентов многочленов числителя и знаменателя в порядке убывания степеней s.

Например, оператор W = tf ([2 1], [1 3 7]) создает объект W подкласса tf, соответствующий передаточной функции ;

zpk – форма нулей, полюсов и коэффициента усиления, которая определяет передаточную функцию (1.19) выражением вида

(1.19)

где k – коэффициент усиления;

z₁, z₂,…, z_m – нули системы, т.е. корни многочлена числителя;

p₁, p₂,…, p_n – полюсы системы, т.е. корни многочлена знаменателя.

Объективно нули полосы имеют отрицательную действительную часть.

В zpk–форме передаточная функция описывается двумя векторами–строками и одним числом, задающими нули, полюсы и коэффициент усиления системы.

Например, оператор W = zpk(0, [-1-j, -1+j, -2], 5) формирует zpk–объект, соответствующий передаточной функции

.

При отсутствии нулей на их место записывается знак «пусто» [ ].

При описании элементов и систем кроме входныхu(t) и выходных y(t) переменных можно выделить некоторые промежуточные переменные x(t), которые связаны с внутренней структурой системы и называются переменными состояния.

В параметрах пространства состояний система n-го порядка с одним входом и одним выходом описывается системой уравнений (1.20)

(1.20)

Здесь А – квадратная матрица порядка n, элементы которой определяются коэффициентами дифференциального уравнения, В – вектор-столбец [n·1] постоянных коэффициентов, С – вектор–строка [1·n] постоянных коэффициентов, D – одноэлементная матрица.

Описание системы в параметрах пространства состояний предусматривает переход от дифференциального уравнения n-го порядка к системе из n дифференциальных уравнений первого порядка и алгебраическому уравнению вход—состояние—выход.

ss–форма представления системы используется для формирования модели в пространстве состояний. Оператор описывает объект W четверкой матриц A, B, C, D, которые должны иметь согласованные размеры.

Пакет ControlSystem содержит ряд команд для временного и частотного анализа, необходимых для проектирования СУ.

Временной отклик.Он описывает переходные процессы в LTI системах во времени при воздействиях на входе и возмущениях на входе. Для этого используются следующие команды (табл. 1.1):

Таблица 1.1

Команды Matlab

Команда	Описание
step	Реакция на ступенчатое воздействие
impulse	Реакция на импульсное воздействие
gensig	Генерация входных сигналов
lsim	Реакция на произвольное заданное воздействие
initial	Реакция на ненулевые начальные условия

Функции step, impulse, initial автоматически выбирают пределы по оси абсцисс для построения переходного процесса. Их синтаксис таков:

step(sys)

impulse(sys)

initial(sys,x0) % x0 – вектор начальных значений переменных состояния.

Автоматический режим выбора пределов времени на графиках можно отменить, задав конечноезначение времени:

step(sys,10) % simulates from 0 to 10 seconds

или вектор равномерно распределенных значений времени отсчета:

t = 0:0.01:10 % отсчет осуществляется каждые 0,01 секунд

step(sys,t)

Частотный отклик.Он позволяет исследовать поведение LTI модели в частотной области и определить полосу пропускания, резонансную частоту, коэффициент усиления на постоянном токе, АЧХ и ФЧХ, устойчивость замкнутой системы.

Для этого используют следующие команды (табл.1.2):

Таблица1.2

Команды Matlab

Команда	Описание
bode	Диаграмма Боде - ЛАЧХ и ЛФЧХ
nyquist	Частотный годограф Найквиста - АФХ
nichols	Частотный годограф Никольса - АФХ в угловых координатах
margin	Запас устойчивости по фазе и модулю

В этих командах диапазон частот выбирается автоматически в зависимости от расположения нулей и полюсов системы. Для задания частотной области точно в интервале {wmin, wmax} используют такой синтаксис команд

bode(sys,{wmin , wmax}) % обратите внимание на фигурные скобки

Можно также задать вектор интересующих частот.

Например,

w = logspace(-1,2,100)

bode(sys,w)

.

Команда logspace задает вектор w логарифмически распределенных частот, начиная с 10^-1 = 0,1 рад/с и заканчивая 10² =100 рад/с, всего 100 точек.

1.2 Порядок выполнения работы

1. Задать в виде tf-модели передаточные функции следующих элементарных звеньев:

– идеального интегрирующего ;

– реального интегрирующего ;

– апериодического ;

– колебательного ;

– форсирующего ;

– интегродифференцирующего .

Параметры звеньев установить в соответствии с вариантом задания(см. табл.1.3).

Tf-модель звена с выбранными параметрами сохранить в отдельном
m-файле с соответствующим именем (например, zveno1) на диске в рабочем каталоге.

2. В созданных и сохраненныхm-файлахс передаточными функциями типовых звеньев реализовать возможность графического представления следующих характеристик этих звеньев:

–переходной функции h(t) – step(zveno1);

–импульсной функции w(t) – impulse(zveno1);

–логарифмических амплитудной и фазочастотных функций L(w) и j(w) – bode(zveno1);

–АФЧХ или частотного годографа Найквиста W(jw) – nyquist(zveno1).

Для форсирующего звена построить графики переходной и импульсной функций не представляется возможным. В отчёте письменно поясните причину такого явления и укажите, как реализуется это звенья на практике.

3. Исследовать влияние коэффициента усиления K на временные и частотные характеристикиинтегрирующего, апериодического и колебательного звеньев. ПараметрыКпринять равным 0,5K, K, 2K.

4. Исследовать влияние постоянной времени T на временные и частотные характеристикиапериодического и колебательного звеньев.Параметры Tпринять равным 0,5T, T, 2T.

5. Исследовать влияние параметра ξ на временные и частотные характеристикиколебательного звена. Параметры ξпринять равным 0,2ξ, ξ, 2ξ.

6. Исследовать влияние постоянной времени T реального интегрирующего звена на временные и частотные характеристики. Параметр Tпринять равным T, 0,1T, 0,01T.Предусмотреть вывод характеристик совместно с характеристиками идеального интегрирующего звена.

7. Построить частотные характеристики для интегро-дифференцирую-щего звена при соотношении T₁>T₂ и T₁<T₂.

1.3 Варианты заданий

Варианты заданий приведены в таблице 1.3.

Таблица 1.3

Варианты заданий

№	К	Т	ξ	Т1	Т2
		0,6	0,3	0,6
		0,8	0,56	0,8
		0,5	0,4	0,5
		1,1	0,75	1,1
		1,2	0,48	1,2
		0,4	0,33	0,4
		0,9	0,64	0,9
		0,5	0,77	0,5
		1,5	0,36	1,5

Окончание табл. 1.3

		0,6	0,5	0,6
		0,7	0,86	0,7
		0,8	0,9	0,8
		0,9	0,6	0,9
			0,45
		1,1	0,92	1,1

1.4 Содержание отчета

Отчет должен содержать следующие разделы:

1.Цель работы.

2.Математические модели динамических звеньев.

3.Графики временные и частотных характеристик.

4.Выводы. Сравнительный анализ результатов моделирования.

1.5Контрольные вопросы

1. Перечислите типовые звенья САУ.

2. Перечислите основные типовые сигналы, применяемые при анализе САУ.

3. Какие временные характеристики звеньев применяют в ТАУ?

4. Какие существуют частотные характеристики звеньев? Объясните их физический смысл, принцип построения.

5. Какие существуют способы математического описания САУ в Matlab?

6. Какие функции анализа статических и динамических характеристик систем существуют в Matlab?

ЛАБОРАТОРНАЯ РАБОТА № 2
ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ систем автоматического управления

Цель работы– изучение особенностей практического использования алгебраических и частотных критериев устойчивости для анализа динамики линейных САУ 3-го порядков в Matlab.

2.1 Краткие теоретические сведения

Устойчивость линейных САУ. Любая система должна быть, прежде всего, работоспособной. Это значит, что она должна нормально функционировать при действии на нее различных внешних возмущений. Иными словами, система должна работать устойчиво, что должно подтверждаться и при анализе ее математической модели.

Понятие устойчивости системы управления связано со способностью возвращаться в состояние равновесия после исчезновения внешних воздействий, которые вывели ее из этого состояния. В общем случае устойчивость САУ определяется характером ее свободного движения.

Устойчивость линейной системы определяется только ее собственными характеристиками и не зависит от действующих на систему возмущений.

Необходимым и достаточным условием устойчивости линейной САУ в общемслучае является нахождение всех корней ее характеристического уравнения в левой половине комплексной плоскости.

Вычисление корней характеристического уравнения высокого порядка затруднительно. Поэтому для исследования устойчивости систем разработаны критерии, позволяющие судить о расположении корней на комплексной плоскости без их расчета. Прежде чем воспользоваться для оценки устойчивости, тем или иным критерием, следует проверить выполнение необходимого условия устойчивости.

Необходимым, но недостаточным условием устойчивости системы является положительность (отрицательность) всех коэффициентов характеристического уравнения системы, т.е. a_i> 0 для всех i от 0 до n, где n- порядок системы.

В ТАУ широко используются алгебраические ичастотные критерии устойчивости. Алгебраические критерии позволяют непосредственно по коэффициентам характеристического уравнения судить об устойчивости систем. В теории управления наибольшее применение из алгебраических критериев устойчивости получили критерий Рауса и критерий Гурвица.

ЛИНЕЙНЫХ СИСТЕМ

Цель работы:

– исследование влияния введения управления по интегралу и производной от ошибки регулирования на точности и качество процессов управления линейных динамических систем.

4.1 Краткие теоретические сведения

Задача синтеза систем автоматического управления (коррекция ихдинамических свойств) состоит в выборе структуры и параметров системрегулирования объектами, которые в соответствии с заданными техническимиусловиями обеспечивают наиболее рациональные характеристики по запасамустойчивости и показателям качества.

Коррекция осуществляется с помощью введения в систему специальных корректирующих звеньев с особо подобранной передаточной функцией.Таким образом, задача синтеза включает в себя определение структуры ипараметров корректирующих звеньев при известных параметрах остальныхзвеньев, входящих в систему, с учетом заданных технических условий.

Корректирующие звенья могут включаться последовательно, параллельно

и в обратной связи. В непрерывных системах автоматического управления используется множество типов корректирующих устройств и в общем случае их структура может быть любой. Однако в теории автоматического управления выделяюттиповые корректирующие звенья, которые называются регуляторами [].

Типовые регуляторы являются наиболее универсальными и распространенными регуляторами. В силу своей универсальности они легко приспосабливаются для автоматизации разнообразных технологических процессов и объектов.

Типовые регуляторы реализуют типовые законы управления.

Закон управления – это алгоритм или функциональная зависимость, в соответствии с которыми регулятор формирует управляющее воздействие u(t).

Эта зависимость может быть представлена в виде:

u(t) = F(e,g,f),

где F– некоторый оператор от сигнала рассогласования e(t), задающего воздействия v(t) и возмущающего воздействия f(t), а также от их производных и интегралов по времени.

Обычно закон управления можно разделить по виду входного сигнала на три слагаемых:

u(t) = F₁(e) + F₂(v) + F₃(f),

где F₁(e), F₂(v) и F₃(f) – выражают управление по отклонению, задающему
и внешнему воздействиям, соответственно.

В зависимости от вида оператора F законы управления делятся настандартные и специальные:

–стандартные законы управления – это универсальные законы, с помощью которых можно решать задачи автоматизации разнообразных технологических процессов и объектов.

– специальные законы управления – это законы, формируемые для решения конкретных задач.

Стандартный закон управления имеет следующий вид:

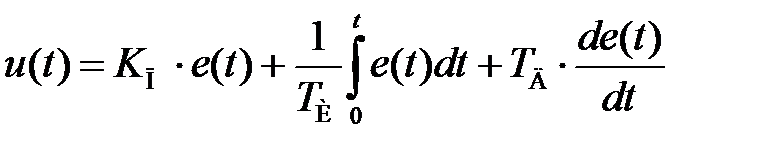(4.1)

Первое слагаемое является пропорциональной, второе – интегральной, третье – дифференциальной составляющими стандартного закона управления.

Коэффициенты K_П, T_ИиТ_Д определяют вклад каждой из составляющих в формируемое управляющее воздействие.

Регулятор, формирующий управляющее воздействие в соответствии со стандартным законом управления имеет передаточную функцию:

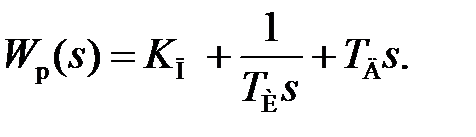(4.2)

Структура регулятора представлена на рис. 4.1.

Рис.4.1

Пропорциональная составляющаястандартного закона управления позволяет уменьшить установившуюся ошибку:

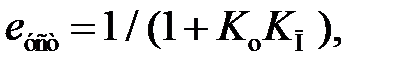
где K_о – коэффициент передачи объекта управления.

Интегральная составляющая стандартного закона управления вводится для повышения степени астатизма системы и, следовательно для повышения точности: e_уст = 0.

Дифференциальная составляющая стандартного закона управления непосредственно не влияет на установившуюся ошибку. Однако она повышает запас устойчивости системы, что позволяет компенсировать потерю устойчивости при увеличении вклада пропорциональной и интегрирующей составляющих.

Кроме того, дифференцирующая составляющая обеспечивает повышение быстродействия и снижение динамической ошибки системы, то есть работает с «предвидением» (предварением).

Рассмотрим типовые алгоритмы управления(законы регулирования), применяемые в линейных автоматических системах.

П (пропорциональный) – регулятор:

Простейший закон регулирования реализуется при помощи безынерционного звена с передаточной функцией

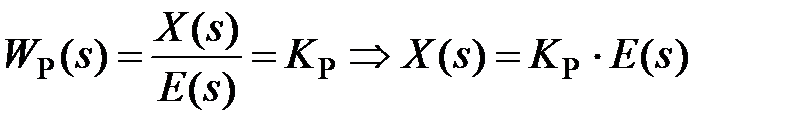. (4.3)

Согласно этому выражению, управляющее воздействие и в статике и в динамике пропорционально сигналу ошибки е. Поэтому такой закон регулирования называется пропорциональным (П).

Преимуществами данного регулятора являются простота и быстродействие, а недостатком – ограниченная точность.

И (интегральный) – регулятор:

Закон регулирования, которому соответствует передаточная функция

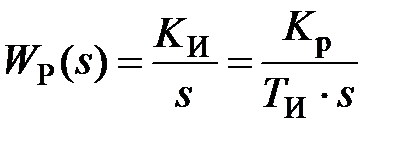, (4.4)

где K_р – коэффициент усиления регулятора;

Т_И – постоянная времени регулятора.

При интегральном управлении получается астатическая система.

Повышение степени астатизма приводит к увеличению установившейся точности системы, но одновременно снижает ее быстродействие, а также приводит к ухудшению устойчивости.

ПИ – регулятор:

Наибольшее распространение в промышленной автоматике получил пропорционально-интегральный(ПИ) закон регулирования

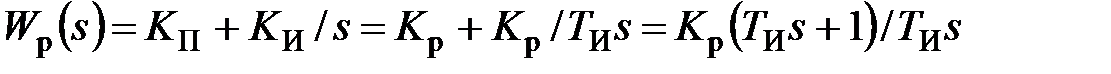. (4.5)

Пропорционально–интегральное (изодромное) управление сочетает в себе высокую точность интегрального управления (астатизм) с большим быстродействием пропорционального управления.

ПД – регулятор:

Наилучшее быстродействие достигается при пропорционально - дифференциальном (ПД) законе регулирования

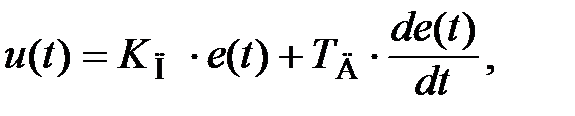
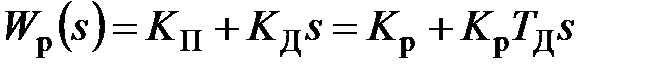. (4.6)

ПД – регулятор реагирует не только на величину сигнала ошибки, но и на скорость его изменения. Благодаря этому при управлении достигается эффект упреждения. Недостатком пропорционально – дифференциального закона регулирования является ограниченная точность.

Пропорционально-дифференциальное управление применяются для
повышения быстродействия работы системы. В результате увеличивается
скорость реакции системы, повышается быстродействие, снижается ошибка в динамике.

ПИД – регулятор:

Наиболее гибким законом регулирования (в классе линейных законов) является пропорционально – интегрально – дифференциальный(ПИД) закон

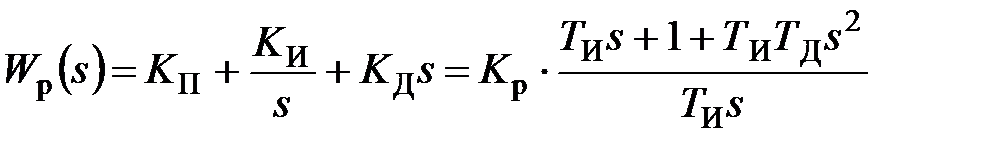, (4.7)

который сочетает в себе преимущества более простых законов.

ПИД–регулятор, представляющий собой астатический изодромный регулятор с предвидением, обеспечивает повышенную точность и повышенное быстродействие системы.

Настройка такого регулятора заключается в задании значений коэффициентов K_П, T_И, T_Д таким образом, чтобы удовлетворить требованиям качества управления в соответствии с выбранными критериями качества.

Существует инженерный подход к синтезу ПИД–регуляторов – методика Зиглера–Николса, которая предполагает следующиешаги:

1.Коэффициенты 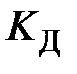и 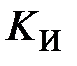устанавливаются равными нулю, а коэффициент 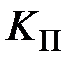увеличивается до тех пор, пока система не потеряет устойчивость.

2.Предельное значение 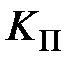обозначается как 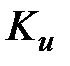, а период автоколебаний как .

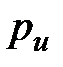3.Значения коэффициентов ПИД – регулятора рассчитываются последующим формулам:

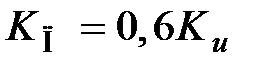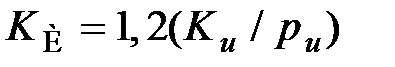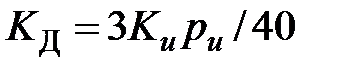, , . (6.3)

В аналоговых промышленных ПИД–регуляторах коэффициенты настраиваются вручную.

4.2 Порядок выполнения работы

На рис. 4.2 - 4.4 представлены схемы набора для исследования процессов регулирования объектами типа апериодическое звено 1-го порядка (рис.4.2) и двойного интегрирующего звена (рис.4.3 и 4.4).

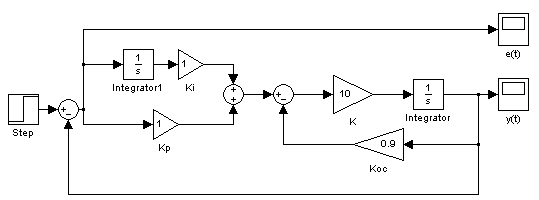
Рис. 4.2 Модель системы с ПИ-регулятором

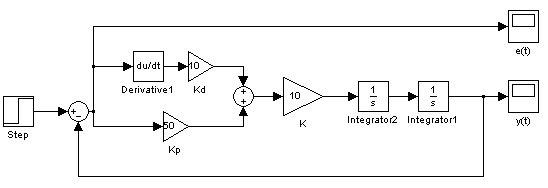
Рис. 4.3 Модель системы с ПД-регулятором

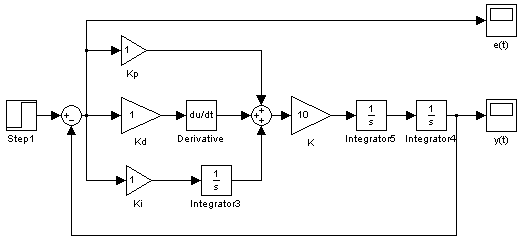
Рис. 4.4 Модель системы с ПИД-регулятором

Для исследования влияния структуры и параметров регулятора на процессы в системе необходимо поочередно рассмотреть САР с различными вариантами регуляторов – П, ПД, ПИ, ПИД при различных значениях коэффициентов передачи.

Порядок выполнения работы следующий:

1. Собрать модель замкнутой САР для апериодического звена 1-го порядка (рис.4.2) с параметрами, заданными в табл. 4.1. На вход системы подать сигнал 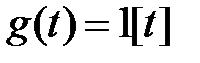. Зарисовать график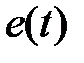и и 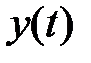исходной нескорректированной системы.

2. Исследовать влияние коэффициентов 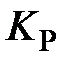и 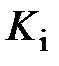на характер изменения функции 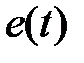. Для этого провести следующие эксперименты:

2.1. Установить 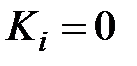. Меняя 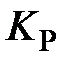определить зависимость статической ошибки, времени регулирования и перерегулирования от величины .

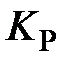2.2.Установить 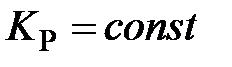. Меняя 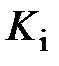оценить эффект от введения интегральной составляющей в закон управления. Зарисовать графики , .

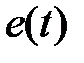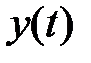По экспериментальным данным сделать выводы о влиянии пропорциональной и интегральной составляющих на процессы регулирования звена 1-го порядка.

3. Собрать модель замкнутой САР для двойного интегрирующего звена (рис. 4.3) с параметрами, заданными в таблице 4.1. На вход системы подать сигнал 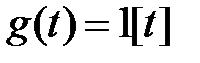. Зарисовать график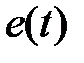и и 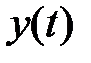исходной нескорректированной системы.

4. Исследовать влияние коэффициентов и на характер изменения функции 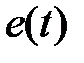. Для этого провести следующие эксперименты:

4.1.Установить . Меняя определить его влияние на .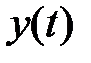

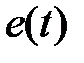4.2.Установить . Меняя оценить эффект от введения дифференциальной составляющей в закон управления. Зарисовать графики и 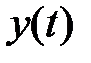. По экспериментальным данным сделать выводы о влиянии пропорциональной и дифференциальной составляющих на процессы регулирования звена.

5. Собрать модель замкнутой САР для двойного интегрирующего звена (рис. 4.4) с параметрами, заданными в табл.4.1. На вход системы подать сигнал 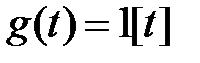. Зарисовать график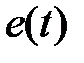и и 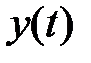исходной нескорректированной системы.

6. Исследовать влияние коэффициентов , и на характер изменения функции . По экспериментальным данным сделать выводы о влиянии пропорциональной, интегральной и дифференциальной составляющих на процессы регулирования звена.Подобрать параметры ПИД–регулятора, обеспечивающие в системе заданные показатели качества ( , ) и запасы устойчивости (табл. 4.2).

Варианты заданий представлены в табл.4.1.

Таблица 4.1

Варианты заданий

№ варианта	Значения параметров
		0.9
		0,8
		0,7
		0,6

Окончание табл. 4.1

		0,5
		0,6
		0,7
		0,8
		0,9
		0,9
		0,8
		0,7
		0,8

Таблица 4.2

Требование к системе

№ варианта Параметр
tрег, c ≤				2,5	3,5		2,5
σ, % ≤
№ варианта Параметр
tрег,c ≤	3,5	3,5				2,5	2,5
σ, % ≤

4.3 Содержание отчета

1. Цель работы.

2.Схемы моделирования исследуемых систем.

3. Полученные графики для каждого пункта.

4.Выводы о влиянии варьируемой составляющей закона регулирования на точность и качество процессов по результатам эксперимента.

4.4 Контрольные вопросы

1. Запишите выражение, реализующее ПИД–регулятор.

2. Как влияют составляющие ПИД–регулятора на качественные характеристики системы?

3. Каким образом настраиваются коэффициенты ПИД–регулятора?

4.

лабораторная работа №5
синтез регулятора в одноконтурной скоростной

Системе постоянного тока

Цель работы:

– изучение метода расчета параметров регуляторов при настройке одноконтурной системы на технический оптимум.

5.1 Краткие теоретические сведения

Электроприводы постоянного тока являются наиболее распространенными объектами регулирования различных автоматических систем. В зависимости от назначения в приводах осуществляется регулирование либо скорости вращения, либо угла поворота (величины перемещения).Типовым примером привода с регулированием скорости вращения являются приводы главного движения различных обрабатывающих станков, которые обеспечивают заданную величину перемещения инструмента. Причем в этих приводах помимо регулирования величины перемещения осуществляется регулирование и стабилизация скорости перемещения.

Для обеспечения высокого качества работы электропривода системы управления строятся по принципу систем подчиненного регулирования с регуляторами тока, скорости и положения.

Это позволяет осуществить регулирование тока якоря, скорости вращения и положения отдельными регуляторами, выбирать желаемые законы регулирования и рассчитывать параметры настроек регуляторов для каждого контура.

При этом обеспечивается раздельная настройка регуляторов и коррекция переходных процессов в каждом контуре.

Функциональная схема трехконтурной системы регулирования электропривода приведена на рис. 5.1.

Рис.5.1

На рисунке: РП, РС, РТ – регуляторы положения, скорости, тока; ДП, ДС, ДТ – датчики положения, скорости, тока; , , – сигналы задания, положения, скорости, тока; УМ – усилитель мощности; ДВ – двигатель.

При проектировании и расчете систем управления электроприводами выбор закона регулирования и расчет параметров настройки регуляторов обычно стремятся сделать так, чтобы получить технически оптимальный переходный процесс (расчет на технический оптимум).

Технически оптимальным переходным процессом считается процесс, обеспечивающий минимальное время достижения согласованного положенияt₁ при перерегулированииσ<(4÷10)% (процесс 2 на рис.5.2.)

Рис.5.2

Для получения переходных процессов, изображенных на рис. 5.2, передаточная функция разомкнутого контура должна иметь вид

, (5.1)

а замкнутый контур будет описываться передаточной функцией колебательного звена

(5.2)

В зависимости от величины (коэффициента затухания ) можно получить процессы вида 1, 2 и 3.При получим процесс вида 1(рис.5.2).

При – процесс вида 2 с временем первого согласования .При =1 – процесс колебательный типа 3.

Для получения технически оптимального переходного процесса характеристическое уравнение замкнутого контура должно иметь вид

, (5.3)

т.е. соответствовать колебательному звену с коэффициентом затухания ξ = 0,707.

В лабораторной работе рассматривается одноконтурная скоростная система управлении. Структурная схема системы представлена на рисунке 5.3.

Объектом управления является исполнительный двигателем постоянного тока (ДПТ), управляемый по цепи якоря.Двигатель постоянного тока управляется от силового регулятора, представленного звеном W_ср(s). Силовой регулятор (в данном случае реверсивный широтно-импульсный преобразователь) управляется от регулятораcпередаточной функциейW_p(s), на вход которого подается разность сигнала управления и обратной связи по скорости.

Рис.5.3

Передаточная функция двигателя постоянного тока получается на основании уравнений, которыми описываются электромагнитные и электромеханические процессы.Схема двигателя изображена на рис. 5.4.

Рис.5.4

На рисунке:

U, I – напряжение, приложенное к якорю и ток якоря;

напряжение и ток возбуждения;

сопротивление и индуктивн