Достаточное условие разложимости функции в ряд Тейлора.

Сформулируем утверждение, с помощью которого будет решена поставленная задача.

Если функция в некоторой окрестности точки х₀ имеет производные до (n+1)-го порядка включительно, то в этой окрестности имеет место формула Тейлора

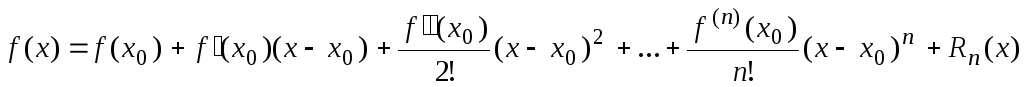
где R_n(х)-остаточный член формулы Тейлора – имеет вид (форма Лагранжа)

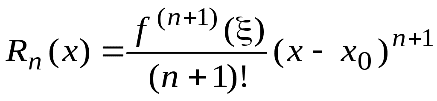
гдеточка ξ лежит между х и х₀.

Отметим, что между рядом Тейлора и формулой Тейлора имеется различие: формула Тейлора представляет собой конечную сумму, т.е. п -фиксированное число.

Напомним, что сумма ряда S(x) может быть определена как предел функциональной последовательности частичных сумм S_п(x)на некотором промежутке Х:

.

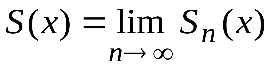Согласно этому, разложить функцию в ряд Тейлора означает найти такой ряд, что для любого х ÎX

Запишем формулу Тейлора в виде , где

.

Заметим, что 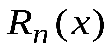определяет ту ошибку, которую мы получаем, заменяй функцию f(x) многочленом S_n(x).

Если 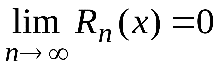, то ,т.е. функция разлагается в ряд Тейлора. Инаоборот, если , то .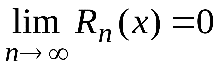

Тем самыммы доказали критерий разложимости функции в ряд Тейлора.

Для того, чтобы в некотором промежутке функция f(х) разлагалась в ряд Тейлора, необходимо и достаточно, чтобы на этом промежутке 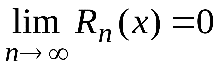, где R_n(x) - остаточный член ряда Тейлора.

С помощью сформулированного критерия можно получить достаточные условия разложимости функции в ряд Тейлора.

Если в некоторой окрестности точки х₀ абсолютные величины всех производных функции ограничены одним и тем же числом М ≥ 0, т.е.

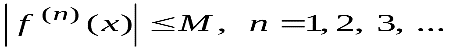, то в этой окрестности функция разлагается в ряд Тейлора.

7. Разложение в ряд Тейлора функций sinx, cosx, ex, ln(1+x), (1+x)m.

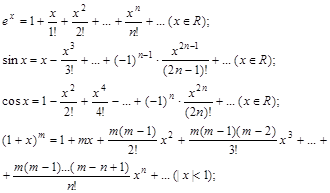
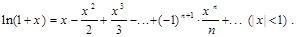
Ряд Фурье для данной функции. Вычисление коэффициентов Фурье. Теорема Дирихле.

Часть – СЛУЧАЙНЫЕ СОБЫТИЯ

Алгебра событий.

Рассмотрим основные операции над событиями и понятие алгебры событий. Пусть - некоторое событие.

1. Дополнением события называется событие , состоящее в том, что событие не произошло. Операциям над событиями можно давать простую геометрическую интерпретацию. Рассмотрим такую интерпретацию операции дополнения. Пусть эксперимент состоит в случайном бросании точки на плоскость, при этом множество условий таково, что исход каждого опыта – это попадание точки в область плоскости.

По определению – это событие, состоящее в том, что не произошло. Поэтому в данной интерпретации – это непопадание точки в область , то есть – попадание точки в заштрихованную область, рис.4.1.

2. Объединением (или суммой) двух событий и называется третье событие , состоящее в том, что произошло хотя бы одно из событий или . Для объединения будем использовать обозначение 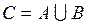или . Признаком операции объединения двух событий может служить союз "или" между ними. Операции объединения, аналогично дополнению, можно дать геометрическую интерпретацию. Пусть – событие, состоящее в том, что случайно брошенная на плоскость точка попала в область, обозначенную также , рис. 4.2. Аналогично событие – это попадание точки в область . Операция объединения определяется для произвольного числа событий. Например, событие 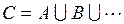состоит в том, что происходит хотя бы одно из событий , … . Событие состоит в том, что происходит хотя бы одно из событий … 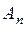. Очевидно операция объединения коммутативна по определению: 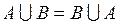и ассоциативна, что также следует из определения: .

3. Пересечением (или произведением) двух событий и называется третье событие , состоящее в том, что произошли оба события и . Для обозначения операции пересечения будем использовать обозначения или . Операция пересечения, также, как и операция объединения, определяется для произвольного числа событий. Например, событие 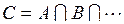состоит в том, что происходят все события 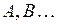Событие 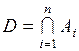состоит втом, что происходят все события 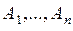. По определению операция пересечения коммутативна, то есть выполняется условие: 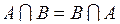, а также ассоциативна:

.

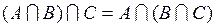Операции объединения и пересечения взаимно дистрибутивны. В частности, операция объединения дистрибутивна относительно пересечения:

.

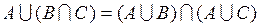Отметим, что если в для операции объединения используется знак "+", а для пересечения – отсутствие знака, то принимает хорошо знакомый вид: – закона дистрибутивности умножения относительно сложения в алгебре чисел. В отличие от этого закон дистрибутивности сложения относительно умножения не имеет аналога в алгебре чисел.Рассмотренные операции над событиями носят алгебраический характер. Поэтому в теории вероятностей важное значение имеет алгебра событий, которая определяется следующим образом.Система событий называется алгеброй событий, если для любой пары событий и из условий следует, что события , , , содержатся в .

Говорят, что алгебра событий – это система событий, замкнутая относительно операций дополнения, пересечения и объединения.