Расчеты сжатых стержней на устойчивость

При помощи коэффициента уменьшения основного

Допускаемого напряжения на сжатие

Для сжатых стержней проводим две проверки:

на прочность:

на устойчивость:

Допускаемое напряжение на устойчивость и допускаемое
напряжение на прочность взаимно связаны. Составим отношение:

где коэффициент уменьшения основного допускаемого напряже-

ния на простое сжатие (коэффициент продольного изгиба). Он

всегда меньше единицы.

Коэффициент 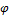зависит от материала стержня и гибкости и принимается по таблицам. Условие устойчивости принимает вид:

При расчете стержня на устойчивость местные ослабления сечений практически не влияют на величину критической силы, поэтому в расчетные формулы вводится полная площадь поперечного сечения A_бpутто.

Различают два вида расчетов на устойчивость сжатых стержней: проверочный и проектировочный.

Проверочный расчет сжатых стержней.

Порядок расчета.

1. Зная размеры и форму поперечного сечения, определить площадь поперечного сечения F_бpуттои минимальный момент инерции J_min.

2. Вычислить минимальный радиус инерции и гибкость стержня по формулам:

3. По таблице найти значение коэффициента .

4. Проверить условие устойчивости

Проектировочный расчет сжатых стержней.

Условие устойчивости содержит две неизвестные величины, которые зависят одна от другой, – площадь поперечного сечения и коэффициент продольного изгиба . Задача при проектировочном расчете сжатых стержней решается методом последовательных приближений. В первом приближении принимают = 0,5, находят площадь сечения и устанавливают фактическое значение .

При большом различии между и выполняется второе приближение, т. е.

до тех пор пока разница в значениях между будет не более 5 %.

Далее окончательно определяются геометрические параметры поперечного сечения стержня.

Выбор материалов и рациональной формы поперечных

Сечений сжатых стержней

Для стержней большой гибкости

модуль упругости Е является единственной механической характеристикой материала, определяющей критические напряжения. Так как модули упругости Е для различных сталей почти одинаковы, то применять высокопрочные стали для гибких стержней нецелесообразно.

Для стержней малой гибкости (они не теряют устойчивости, а разрушаются от простого сжатия) использование сталей повышенной прочности будет целесообразным.

Так как продольный изгиб происходит всегда в плоскости наименьшей жесткости, то при проектировании сжатых стержней необходимо стремиться к тому, чтобы главные моменты инерции были по возможности одинаковыми. Поэтому применять двутавровые и сплошные прямоугольные сечения нерационально. При заданной площади сечения выгоднее будет такое сечение, у которого материал распределен по возможности дальше от главных центральных осей инерции. Поэтому кольцевое сечение в этом отношении значительно выгоднее, чем сплошное круглое. Рациональными являются и коробчатые тонкостенные сечения. Однако при значительном уменьшении толщины стенок пустотелых стержней может произойти местная потеря устойчивости, для предотвращения которой ставят ребра жесткости (рис. 12.10, ж).

Самой экономичной конструкцией сжатых стержней являются решетчатые стержни.

Для стержней, у которых осевые моменты инерции различны, добиться равной устойчивости в двух плоскостях можно при различном закреплении концов стержня.

Рис.12.10. Схемы рациональных поперечных сечений сжатых стержней

Пример расчета

ЗАДАЧА №1

Стальной стержень (сталь 3) прямоугольного поперечного сечения сжат силой F (рис. 12. 11). Один конец стержня жестко закреплен, а второй свободен (μ=2). Определить величину допускаемой силы F, если [σ]=160 МПа, величину критической силы и допускаемый коэффициент запаса устойчивости.

РЕШЕНИЕ:

1. Определим геометрические характеристики поперечного сечения:

Рис. 12. 11. Схема для расчета сжатого стального стержня на устойчивость

2. Определим гибкость стержня:

3. Согласно табличных значений (приложение 5), методом линейной интерполяции определим коэффициент продольного изгиба:

4. Определим величину допускаемой силы F из условия устойчивости:

5. Определим критическую силу по формуле Эйлера, так как :

6. Определим коэффициент запаса устойчивости:

ЗАДАЧА №2

Подобрать двутавровое поперечное сечение стержня длиной 4,5 м под сжимающую нагрузку F=750 кН (рис.12.12). Оба конца стержня жестко защемлены (μ=0,5). Материал стержня – сталь 3. Допускаемое напряжение на сжатие [σ]=160 МПа.

РЕШЕНИЕ:

Рис. 12.12. Схема двутавровой стойки

Задачу решаем методом последовательных приближений.

1. Первое приближение. Принимаем тогда имеем:

Из таблицы сортамента ГОСТ 8239-72 подбираем двутавр № 45, которого A=84,7 см²; i_min=3,09 см. Определим гибкость стержня:

Линейной интерполяцией по таблице (приложение 5) находим:

2. Второе приближение:

Из таблицы сортамента подбираем двутавр № 40, у которого F=72,6 см²; i_min=3,03 см. Находим гибкость стержня:

3. Третье приближение:

Из таблицы сортамента подбираем двутавр № 36, у которого F=61,9 см²; i_min=2,89 см. Определим гибкость стержня:

4. Проверяем условие устойчивости подобранного сечения по формуле:

Окончательно принимаем двутавр №36.

ЗАДАЧА №3

Колонна двутаврового поперечного сечения №30а (рис. 12.13) жестко защемлена обоими концами (μ=0,5). Длина колонны 3,6 м. Определить максимальное значение допускаемой силы, если [σ]=150 МПа.

РЕШЕНИЕ:

1. Задаемся μ=0,5. Из таблицы сортамента ГОСТ 8239-72 находим для двутавра №30а A=49,9 см²; i_min=i_у =2,95 см.

2. Определим гибкость колонны:

Рис. 12.13. Схема двутавровой колонны

3. Линейной интерполяцией по таблице (приложение 5) определим коэффициент продольного изгиба (коэффициент снижения допускаемого напряжения на сжатие):

4. Из условия устойчивости определим допускаемую силу:

ЗАДАЧА №4

Стойка, изготовленная из стали 3, имеет прямоугольное поперечное сечение b´h=20×40 мм и сжата силой F=64 кН (рис.12.14). Одно из сечений стойки ослаблено отверстием диаметром d=10 мм. Проверить прочность и устойчивость стойки, если [σ]=160 МПа.

РЕШЕНИЕ:

1. Определяем площадь сечения A_нетто:

2. Проверяем прочность:

3. Определяем необходимые геометрические характеристики:

Рис. 12.14. Схема стальной стойки с ослабленным поперечным сечением

4. Определяем гибкость:

По таблице (приложение 5) находим

5. Проверяем устойчивость стойки:

Устойчивость стойки обеспечена.

ЗАДАЧА №5

Стальной стержень квадратного поперечного сечения жестко закреплен между двумя опорами (рис. 12.15). Как изменится величина критической силы, если оба его конца закрепить шарнирно (μ=1)?

РЕШЕНИЕ:

Рис. 12.15. Схема стального стержня квадратного поперечного сечения

1. Определим геометрические характеристики поперечного сечения:

2. Первый случай закрепления:

3. Для определения критической силы применим формулу Ясинского:

,

где а=310 МПа, b=1,14 МПа – коэффициенты, которые определяются экспериментальным путем и имеют размерность напряжений.

4.Второй случай закрепления:

5. Для определения критической силы применим формулу Эйлера:

6. Критическая сила во втором случае уменьшилась в

12.9. Задачи для самостоятельного решения

ЗАДАЧА №6

Определить наибольшую допускаемую величину сжимающей силы F на деревянную стойку круглого поперечного сечения диаметром d=200 мм при допускаемом напряжении [σ]=10 МПа. Длина стойки Оба конца ее шарнирно оперты (рис.12.16).

Рис. 12.16. Схема деревянной стойки

ОТВЕТ: [F] = 150кН

12.10. Контрольные вопросы

1. В чем заключается явление потери устойчивости сжатого стержня?

2. Какая сила называется критической силой?

3. Какое дифференциальное уравнение из теории изгиба лежит в основе вывода формулы Л. Эйлера?

4. Что называется гибкостью стержня? Приведите формулу.

5. Приведите формулу Л. Эйлера для определения критической силы?

6. Как учитывается различное закрепление концов стержня при определении критической силы?

7. Каков предел применимости формулы Л. Эйлера?

8. Как определяется предельная гибкость для формулы Л. Эйлера?

9. Как определяется критическая сила при напряжениях, превышающих предел пропорциональности материала?

10. Какой вид имеет график изменения критической силы в зависимости от гибкости (или длины) для стальных стержней?

11. Приведите формулу Ф. Ясинского для определения критической силы и укажите пределы её применимости.

12. Как определяется коэффициент запаса устойчивости сжато-

го стержня?

13. Напишите условие устойчивости сжатого стержня через критическую силу и коэффициент запаса устойчивости.

14. Напишите условие устойчивости сжатого стержня с помощью коэффициента продольного изгиба j.

15. От чего зависит коэффициент продольного изгиба j, и в каких пределах он изменяется?

16. Какие три типа задач можно решать исходя из условия устойчивости сжатого стержня?

17. Покажите порядок подбора сжатого стержня из условия устойчивости с помощью коэффициента j.

Динамические нагружения