Критическая сила. Формула Эйлера. Влияние закрепления концов стержня на величину критической силы

Рассмотрим стержень постоянного сечения, оба конца которого закреплены шарнирно (рис. 12.3). Стержень сжимается критической силой. Рассматриваем малые перемещения сечений стержня. Задавшись прогибом оси стержня в определенном сечении, найдем величину осевой сжимающей силы, при которой такой прогиб возможен. Будем считать, что напряжения в стержне не превышает предела пропорциональности.

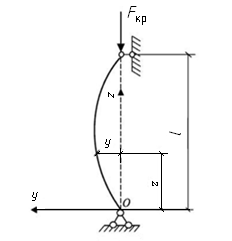
Рис. 12.3. Схема изгиба стержня критической силой F_кр.

Начало координат поместим в точке О, ось z направлена вдоль оси стержня, ось y – влево от начала координат. Определим прогиб стержня в произвольном сечении z.

Воспользуемся приближенным дифференциальным уравнением изогнутой оси стержня:

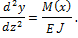
Определим изгибающий момент в произвольном сечении стержня:

тогда

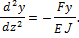
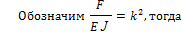
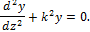
Последнее выражение представляет собой однородное дифференциальное уравнение с постоянными коэффициентами.

Решение этого уравнения можно записать в виде гармонической функции:

у = Asinkz +Bcoskz.

Постоянные интегрирования А и В находятся из граничных условий:

при z = 0, у = 0, В = 0 и дифференциальное уравнение принимает следующий вид:

y = Asinkz.

Стержень изгибается по синусоиде.

При z = l, у = 0 Asinkl = 0.

Известно, что произведение двух сомножителей равно нулю, лишь в том случае, если один из сомножителей равен нулю. Разберем оба случая.

Пусть А = 0, то у(z) всегда равен нулю и прогиба вообще не существует. Это решение противоречит принятому предположению о том, что стержень прогнулся, т. е. А 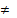0. Следовательно, должно выполняться условие sinkl = 0, откуда:

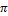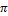kl = 0, , 2 , 3 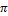, …, n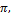

где п – любое целое число.

Определим, какое значение п подходит к решению данной задачи. Рассмотрим условие

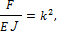
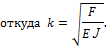
Из последнего выражения следует, что если k = 0, то F_кр =0, т. е. стержень не нагружен, а это противоречит условию задачи. Следовательно, значение k = 0 можно исключить из решения. В общем случае имеем:

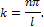
Приравняв F = F_кр, получим выражение

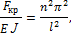
откуда

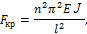
где 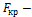наименьшее значение сжимающей силы, при котором проис-

ходит продольный изгиб, поэтому следует принять п = 1.

Тогда уравнение для определения критической силы примет вид

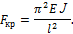
Таким образом, стержень изгибается по синусоиде с одной полуволной.

При z = l/2 прогиб стержня имеет максимальное значение.

При n = 2 и n = 3 стержень изгибается по двум и трем полуволнам синусоиды соответственно (рис. 12.4, б, в).

Прогиб стержня в произвольном сечении под воздействием сжимающей силы можно определить по формуле

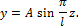
Потеря устойчивости стержня происходит в плоскостях наименьшей жесткости, т. е. J = J_min, поэтому при определении критической силы следует учитывать наименьший осевой момент инерции сечения, тогда окончательно:

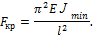
Таким образом, имеем формулу Эйлера (1744) для определения критической силы для стержня с двумя шарнирно закрепленными концами (основной случай).

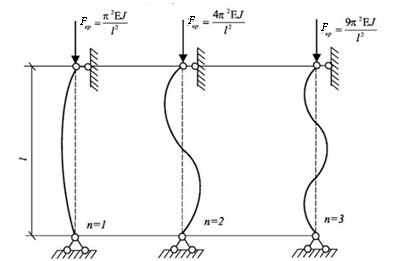
Рис. 12.4. Схема изогнутой оси стержня при различных значениях n

Величина критической силы прямо пропорциональна наименьшей жесткости сечения и обратно пропорциональна квадрату длины стержня.

Как видно из формулы Эйлера, величина критической силы зависит от геометрических характеристик стержня и модуля упругости материала, но не зависит от прочностных характеристик материала.

Так, например, критическая сила F_кр практически не зависит от марки стали.

Предельная растягивающая сила зависит от прочностных характеристик (в зависимости от марки стали она будет различной) и не зависит от длины стержня. Таким образом, можно утверждать, что имеется существенное различие между работой стержня на растяжение и сжатие.

Выше был рассмотрен так называемый основной случай закрепления концов сжатого стержня, когда оба конца стержня закреплены шарнирно. На практике применяются и другие способы закрепления концов стержня.

Рассмотрим, как влияют условия закрепления стержня на величину критической силы.

Второй случай: один конец стержня жестко защемлен, второй – свободен (рис. 12.5, а).

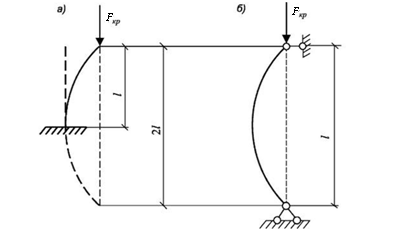
Рис. 12.5. Схема закрепления стержня по второму случаю

При потере устойчивости верхний конец стержня отклонится на некоторую величину и повернется, нижний защемленный конец останется вертикальным. Изогнутая ось получится такая же, как для одной половины стержня первого случая (рис. 12.5, б).

Для получения полного соответствия с первым случаем продолжим мысленно изогнутую ось стержня вниз. Тогда форма потери устойчивости будет полностью совпадать с первым случаем. Отсюда можно сделать вывод, что критическая сила для этого случая будет такая же, как и для пропорционально закрепленного по концам стержня длиной 2 м. Тогда

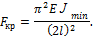
Третий случай: оба конца стержня жестко закреплены (рис. 12.6).

После потери устойчивости концы стержня не поворачиваются. Средняя часть стержня длиной l/2 вследствие симметрии будет работать в таких же условиях, что и стержень с шарнирно опертыми концами, но длиной l. Тогда, исходя из формулы, получим:

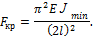
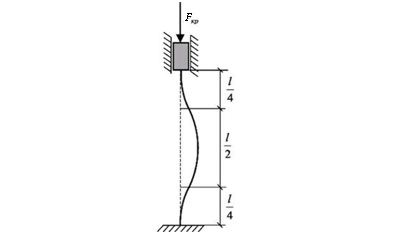
Рис. 12.6. Схема закрепления стержня

по третьему случаю

Четвертый случай: один конец стержня жестко защемлен, а другой – закреплен шарнирно. В этом случае верхняя часть стержня длиной приблизительно 2l/3 имеет вид полуволны синусоиды и находится в таких же условиях, что и стержень с шарнирными опорами на концах (рис. 12.7).

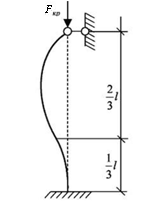
Рис. 12.7. Схема закрепления стержня

по четвертому случаю

Тогда

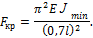
Анализируя последние выражения для определения критической силы, приходим к выводу, что чем более жестко закреплены концы стержня, тем большую нагрузку данный стержень может воспринимать.

Поэтому зависимости для определения критической силы при различных условиях закрепления стержня можно объединить в одну формулу:

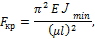
где 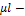приведенная длина стержня;

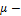коэффициент приведения длины стержня, зависящий от способа

закрепления концов стержня;

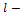фактическая длина стержня.

Понятие о приведенной длине стержня впервые было введено профессором Петербургского института путей сообщения Ф. С. Ясинским в 1892 году.

Необходимо также отметить, что при составлении формул для определения критических сил в стержнях с различными условиями закрепления по концам использовалась аналогия в формах потери устойчивости отдельных их участков.

Однако эти решения можно получить также строго математически. Для этого необходимо записать для каждого случая дифференциальное уравнение упругой линии стержня при потере устойчивости и решить его с использованием граничных условий.

Коэффициент продольной длины стержня в зависимости от условий его закрепления представлен на рис. 12.8.

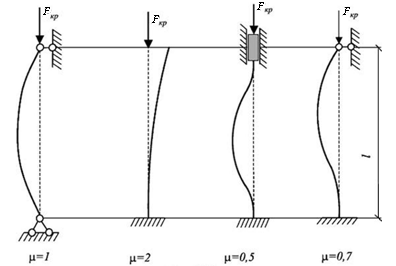
Рис.12.8. Коэффициент приведения длины для различных случаев

закрепления концов стержня