Определение положения опасного сечения и диаметра вала

С использованием третьей и четвертой теорий прочности

По эпюрам М_кр и М_и находим опасное сечение и определяем максимальный расчетный момент.

Опасным сечением вала следует считать то, где суммарный изгибающий и крутящий моменты одновременно имеют большое значение.

В тех случаях, когда М_кр и М_и имеют большое значение в разных сечениях, необходимо в каждом из сечений подсчитать величину расчетного момента и принять для дальнейшего расчета наибольшее из полученных значений.

Материал вала находится в условиях плоского напряженного состояния, которое создается нормальными напряжениями изгиба и касательными напряжениями кручения. Поэтому величину расчетного момента определяем по одной из принятых теорий прочности. Значения расчетных моментов для стальных валов определяем по следующим формулам:

по третьей теории прочности

по четвертой теории прочности

Расчетный момент для вала из хрупкого материала (дерево, чугун): по второй теории прочности

где М_и и М_кр – суммарный изгибающий и крутящий моменты в опасном сечении вала соответственно.

Если известны величина расчетного момента М_р (кНсм) и допускаемое напряжение [σ] (кН/см²), то из условия прочности можно найти диаметр вала по формуле

см³.

Таким образом, необходимый диаметр вала рассчитывается по формуле

Полученный диаметр вала следует округлить до ближайшего стандартного значения линейного ряда размеров.

размеры кольцевого сечения вала определяются из условия прочности аналогичным образом:

где 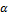– отношение внутреннего диаметра вала к наружному.

С учетом последнего выражения определим диаметр вала по формуле

Пример расчета

Задача 1. Стальная балка прямоугольного поперечного сечения нагружена, как указано на схеме (рис. 11.14). Допускаемые напряжения [σ] = 160 МПа. Проверить прочность балки в двух сечениях: при α = 20˚ и при α = 0. Сравнить результаты расчета.

Рис. 11.14. Схема защемленной балки при косом изгибе

Решение.

1. Определим геометрические характеристики сечения балки:

2. Определим проекции силы F на координатные оси:

случай нагружения α = 20˚:

3. Определим максимальное нормальное напряжение:

тогда из условия прочности имеем:

Прочность балки не обеспечена.

4. Определим проекции силы F на координатные оси:

случай нагружения α = 0˚:

тогда

Прочность балки обеспечена.

Сравниваем результаты расчета:

Задача 2. Проверить прочность изображенной на схеме балки (рис. 11.15), если [σ] = 160 МПа.

Рис. 11.15. Схема защемленной балки при косом изгибе

Решение.

1. Определим геометрические характеристики поперечного сечения:

2. Определим максимальное нормальное напряжение:

3. Проверим условие прочности:

Условие прочности соблюдается.

Задача 3. Двутавровая балка № 20 длиной l = 1,4 м нагружена на консоли сосредоточенной силой F = 4 кН, направление которой составляет угол 30º с главной осью инерции сечения (рис. 11.16). Определить нормальные напряжения в угловых точках защемленного сечения и построить эпюру нормальных напряжений.

Рис. 11.16. Схема двутавровой балки при косом изгибе

Решение.

1. Из сортамента ГОСТ 8239–72 для двутавра № 20 находим:

2. Определим изгибающие моменты, действующие в главных плоскостях инерции двутавровой балки:

3. Определим нормальные напряжения в угловых точках защемленного поперечного сечения по формуле

окончательно получим:

Задача 4. Деревянная балка нагружена, как указано на схеме (рис. 11.17). Определить размеры поперечного сечения балки, если [σ] = 10 МПа.

Рис. 11.17. Схема деревянной балки для определения размеров

поперечного сечения при косом изгибе

Решение.

1. Определим геометрические характеристики поперечного сечения:

2. Определим значение изгибающих моментов:

3. Условие прочности для защемленного сечения балки:

Задача 5. Определить наибольшую величину силы F (рис. 11.18), которую можно приложить к стальной балке, если допускаемое напряжение [σ] = 160 МПа. Чему будет равен максимальный прогиб при этом значении силы?

Рис. 11.18. Схема консольной стальной балки при косом изгибе

Решение.

1. Определим геометрические характеристики поперечного сечения:

2. Из условия прочности имеем:

откуда .

3. Определим максимальный прогиб балки при F = 297 кН:

Задача 6. Колонна прямоугольного поперечного сечения нагружена в точке А сжимающей силой F = 120 кН (рис. 11.19). Определить напряжения в угловых точках сечения и построить эпюру нормальных напряжений.

Рис. 11.19. Схема колонны для определения напряжений

в угловых точках сечения

Решение.

1. Определяем геометрические характеристики поперечного сечения:

площадь поперечного сечения:

моменты сопротивления поперечного сечения:

2. Определим внутренние силовые факторы:

3. Находим напряжения в угловых точках прямоугольного сечения по формуле

Окончательно находим:

Задача 7. Деревянный брус прямоугольного поперечного сечения
b ´ h = 50 ´ 60 мм (рис. 11.20) растягивается приложенной вдоль оси силой F = 10 кН. Проверить прочность бруса для двух случаев:

1) брус ослаблен двумя вырезами глубиной 20 мм;

2) брус ослаблен одним вырезом с той же глубиной.

Допускаемое напряжение [σ] = 10 МПа.

Рис. 11.20. Схема деревянного бруса

Решение.

1-й случай (центральное растяжение):

2-й случай (внецентренное растяжение):

Во 2-м случае прочность не обеспечена. Нормальные напряжения увеличились на 25 %.

Задача 8.Проверить прочность нижней части бетонной колонны (рис. 11.21), имеющей прямоугольное поперечное сечение b ´ h = 180 ´ 200 мм. Допускаемое напряжение на растяжение [σ]_р = 0,6 МПа, на сжатие [σ]_сж = 7 МПа.

Рис. 11.21. Схема бетонной колонны при внецентренном сжатии

Решение.

1. Определим геометрические характеристики сечения:

2. Определим внутренние силовые факторы:

3. Определим нормальные напряжения:

Условие прочности соблюдается.

Задача 9. Стальной вал диаметром d = 75 мм опирается на подшипники и приводится во вращение от двигателя с угловой скоростью ω = = 20 рад/с (рис. 11.22). Передаваемая на вал мощность N = 50 кВт. На валу насажен шкив, диаметр которого D = 0,8 м и вес G = 0,6 кН. Через шкив переброшен ремень, ветви которого параллельны и наклонены к горизонту под углом 30º. Натяжения ветвей равны 2t и t. Проверить прочность вала по четвертой теории прочности, если [σ] = 80 МПа.

Рис. 11.22. Схема вала при совместном действии изгиба с кручением

Решение.

1. Определим крутящий момент, передаваемый с электродвигателя на шкив ременной передачи:

2. Определим усилие натяжения набегающей ветви ремня:

3. Определим усилие, которое передается на вал за счет натяжения ветвей ременной передачи:

4. Определим усилия, которые действуют на вал в главных плоскостях инерции:

5. Построим эпюры изгибающих моментов в вертикальной и горизонтальной плоскостях. Определим опасное сечение, где

.

6. Определим значение суммарного изгибающего момента:

7. Определим значение приведенного расчетного момента по четвертой теории прочности:

8. Определим момент сопротивления сечения вала:

9. Определим напряжения, возникающие в опасном сечении вала:

Прочность вала обеспечена.

11.11. Контрольные вопросы

1. Какой изгиб называется косым?

2. По каким формулам определяются нормальные напряжения при косом изгибе?

3. Как находится положение нейтральной оси при косом изгибе?

4. Что представляют собой опасные точки в сечении и как определяется их положение при косом изгибе?

5. Как определяются перемещения точек оси при косом изгибе?

6. Какой вид нагружения называется внецентренным растяжением (сжатием)?

7. Как определяются нормальные напряжения при внецентренном растяжении (сжатии)?

8. Как определяется положение нейтральной оси при внецентренном растяжении (сжатии)?

9. Чему равняется нормальное напряжение в центре тяжести сечения при внецентренном растяжении (сжатии)?

10. Что называется ядром сечения?

11. Как строится ядро сечения и как определяются его ординаты?

12. Какой вид нагружения называется совместным действием изгиба с кручением?

13. Какие точки поперечного сечения являются опасными при совместном действии изгиба с кручением?

14. Как находится расчетный момент при совместном действии изгиба с кручением? Построение эпюр изгибающих и крутящих моментов.

15. Какие теории прочности используются в расчетах валов при совместном действии изгиба с кручением?

16. Как определяется диаметр вала при совместном действии изгиба с кручением?