Положение опасных точек. Условие прочности

Нейтральная ось делит сечение на две зоны – сжатую и растянутую. Напряжения в точках сечения линейно зависят от расстояния до нейтральной оси. Проведем касательные к контуру сечения, параллельные нейтральной оси, получим точки M и N (см. рис. 11.8). В этих точках возникают максимальные напряжения растяженияисжатия соответственно. Если материал бруса неодинаково сопротивляется растяжению и сжатию (чугун, бетон, каменная кладка), то необходимо составить два условия прочности:

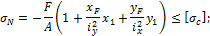
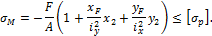
11.7. Понятие о ядре сечения при внецентренном растяжении

(сжатии)

Нейтральная ось в общем случае может проходить через сечение, касаться сечения или находиться за его пределами.

Например, если сила F приложена в центре тяжести сечения, то нейтральная ось проходит в бесконечности и нормальные напряжения в этом случае распределяются равномерно по сечению (центральное растяжение-сжатие).

В некоторых случаях необходимо установить возможные положения сжимающей силы, при которых напряжения во всех точках поперечного сечения будут одного знака. Простейший пример представляет бетонная колонна, на которую опирается балка перекрытия. Так как бетон хорошо работает на сжатие и плохо работает на растяжение, то необходимо приложить внешнюю нагрузку таким образом, чтобы во всех точках сечения возникали только сжимающие напряжения. Следовательно, нейтральная ось в данном случае должна проходить вне сечения или только касаться его.

Область вокруг центра тяжести сечения, характерная тем, что всякая продольная сила, расположенная внутри или по границе этой области, вызывает во всех точках поперечного сечения напряжения одного знака, называется ядром сечения. Если силу приложить на границе ядра сечения, то нейтральная ось будет касательной к контуру сечения.

Для построения ядра сечения необходимо рассмотреть различные положения касательных к контуру сечения, предполагая, что они представляют собой нейтральные линии, и найти координаты граничных точек ядра сечения, а затем по этим точкам построить ядро сечения.

Координаты границ ядра сечения можно определить по формулам:

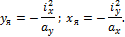
Построения ядра для некоторых сечений рассмотрим на конкретных примерах.

Пример 1. Построить ядро сечения для круга (рис. 11.10). Пусть нейтральная ось совпадает с касательной I–I. Определим отрезки, которые отсекает нейтральная ось на координатных осях:

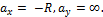
Координаты границы ядра сечения находим по зависимостям:

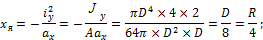
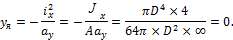
Для симметричного сечения (круг) достаточно рассмотреть одно положение касательной к сечению. Ядром сечения круга также будет круг радиусом R/4 (рис. 11.10).

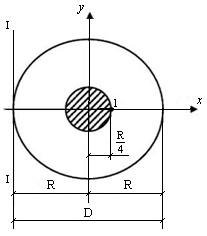
Рис. 11.10. Схема построения ядра

сечения для круга

Пример 2. Построить ядро сечения прямоугольника. Совместим нейтральную ось со стороной АВ (касательная I–I, рис. 11.11):

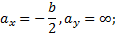
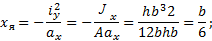
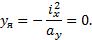
Строим точку 1. Совместим теперь нейтральную ось со стороной BC (касательная II–II).

Координаты касательной II–II и точки 2 соответственно:

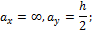
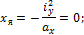
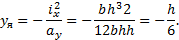
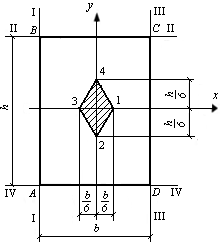
Рис. 11.11. Схема построения ядра сечения

для прямоугольника

Касательная III–III и точка 3:

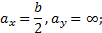
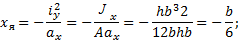
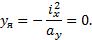
Касательная IV–IV и точка 4:

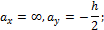
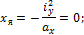
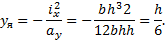
Таким образом, ядром сечения прямоугольника является ромб с диагоналями, равными одной трети соответствующей стороны сечения (рис. 11.11).

11.8. Изгиб с кручением пространственного вала

круглого поперечного сечения

Совместное действие изгиба и кручения является характерным случаем нагружения валов круглого поперечного сечения, которые являются составной частью редукторов, коробок переменных передач, тормозных устройств и т. п.

Силы, действующие на валы (усилия на зубьях шестерен, натяжение ремней шкивов ременных передач, собственный вес валов и шкивов и т. п.) вызывают в поперечном сечении следующие внутренние силовые факторы (ВСФ): .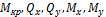

Следовательно, в любом поперечном сечении вала возникают напряжения:

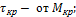
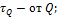
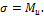
На практике обычно применяются валы круглого поперечного сечения, для которых невозможен косой изгиб. Поэтому в общем случае действия внешних сил вал круглого поперечного сечения испытывает действие прямого поперечного изгиба и кручения. Действием продольных сил N пренебрегаем.

Расчет вала с несколькими шкивами для ременной передачи или зубчатыми колесами начинается с определения величины крутящих моментов, передаваемых на вал по заданной мощности N (квт) и числу оборотов вала n (об/мин). Для определения крутящего момента (кНм) воспользуемся формулой

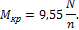
После определения крутящих моментов, используя метод сечений, строим их эпюру. Построение эпюры крутящих моментов производят, двигаясь от одного конца вала к другому, например, слева направо. При этом следует учитывать, что внутренний крутящий момент в любом сечении вала численно равен алгебраической сумме внешних крутящих моментов по одну сторону от рассматриваемого сечения. Будем считать крутящий момент положительным, если со стороны нормали к отсеченной части вала внешний вращающий момент, действующий на эту часть, направлен по ходу часовой стрелки, и отрицательным – против часовой стрелки.

Далее определяем окружные усилия, действующие на шкивы (зубчатые колеса). При этом вес шкивов и зубчатых колес не учитываем.

Силы, которые передаются на вал через шкивы, действуют под определенными углами наклона к горизонтальной оси, проходящей через центр вращения шкива. Каждая их них может быть разложена на две составляющие – горизонтальную и вертикальную. Для ременных передач принимают, что натяжение набегающей ветви ремня равно t, а натяжение сбегающей – 2t.

Следовательно, крутящий момент (кНм), передаваемый шкивом, будет равен:

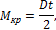
где t – разность натяжений сбегающей и набегающей ветвей ремня, кН;

D – диаметр шкива, м.

Отсюда натяжение набегающей ветви ремня можно определить по формуле

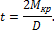
Считаем, что набегающая и сбегающая ветви на шкивах параллельны. Тогда вал в сечениях, где посажены шкивы, будет нагружен силами F = 3t (рис. 11.12).

Силы, изгибающие вал в вертикальной и горизонтальной плоскостях, определяются по формулам:

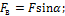
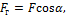
где α – угол наклона ветвей ремня к горизонту.

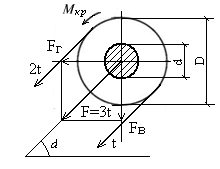
Рис. 11.12. Расчетная схема вала

для определения окружных усилий на шкиве

На расчетной схеме (рис. 11.13) показаны усилия, действующие на зубья колес: окружные – F_t , радиальные – F_r, осевые – F_а.

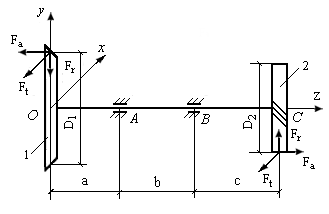
Рис. 11.13. Расчетная схема вала для определения усилий

на зубчатых колесах

Силы, которые передаются на вал через зубчатые колеса, определяются по формулам:

для всех колес окружные усилия:

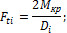
для цилиндрического зубчатого колеса:

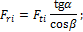
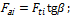
для конического зубчатого колеса:

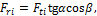
где F_ti – окружная сила на i-м колесе, перпендикулярная оси вала и направленная по касательной к окружности вала диаметром D_i, кН;

F_ri – радиальная сила на i-м колесе, перпендикулярная оси вала и

пересекающая ее, кН;

F_ai – осевая сила на i-м колесе, параллельная оси вала, кН, где a – угол зацепления; b – угол наклона линии зуба; d – угол делительного конуса.

После определения сил, действующих на вал перпендикулярно его оси, строим эпюры изгибающих моментов, действующих в вертикальной и горизонтальной плоскостях. При этом вал рассматривается как простая статически определимая балка на двух опорах.

В вертикальной плоскости линии действия радиальных сил F_ri остаются неизменными. При переносе на ось вала осевых сил F_ai необходимо добавить изгибающие моменты, которые определяются по формуле

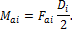
По отношению к осям y и z направления радиальных и осевых сил, а также моментов М_аi в вертикальной плоскости должны соответствовать тем направлениям, которые они имеют на схеме вала. То же самое касается и окружных сил F_ti, действующих в горизонтальной плоскости.

Эпюры изгибающих моментов 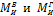от сил, действующих в вертикальной и горизонтальной плоскостях, строим на основании общей схемы построения эпюр изгибающих моментов для однопролетной балки методом сечений.

Суммарный изгибающий момент М_И в любом сечении вала определяется по формуле

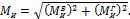
Вычисляя в характерных сечениях значения М_И, строим эпюру суммарных изгибающих момента для вала.

Суммарная эпюра моментов будет прямолинейной на тех участках вала, где 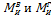по абсолютной величине одновременно убывают или одновременно возрастают. На тех участках, где 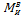возрастает, а 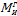убывает (или наоборот, 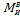убывает, 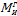возрастает) эпюра суммарных моментов будет криволинейной.