В поперечных сечениях бруса. Нахождение опасного сечения

Косым называют такой вид изгиба, при котором все внешние нагрузки, вызывающие изгиб, действуют в одной силовой плоскости, не совпадающей ни с одной из главных плоскостей.

Рассмотрим брус, защемленный одним концом и загруженный на свободном конце силой F (рис. 11.3).

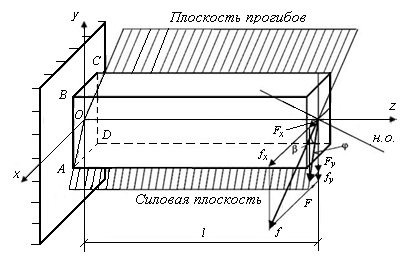
Рис. 11.3. Расчетная схема к косому изгибу

Внешняя сила F приложена под углом 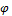к оси y. Разложим силу F на составляющие, лежащие в главных плоскостях бруса, тогда:

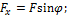
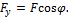
Изгибающие моменты в произвольном сечении, взятом на расстоянии z от свободного конца, будут равны:

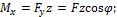
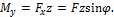
Таким образом, в каждом сечении бруса одновременно действуют два изгибающих момента, которые создают изгиб в главных плоскостях. Поэтому косой изгиб можно рассматривать как частный случай пространственного изгиба.

Нормальные напряжения в поперечном сечении бруса при косом изгибе определяются по формуле

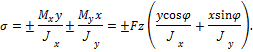
Для нахождения наибольших растягивающих и сжимающих нормальных напряжений при косом изгибе необходимо выбрать опасное сечение бруса.

Если изгибающие моменты |М_х| и |М_у| достигают наибольших значений в некотором сечении, то это и есть опасное сечение. Таким образом,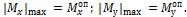

К опасным сечениям относятся также сечения, где изгибающие моменты |М_х| и |М_у| одновременно достигают достаточно больших значений. Поэтому при косом изгибе может быть несколько опасных сечений.

В общем случае, когда 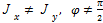– несимметричное сечение, т. е. нейтральная ось не перпендикулярна силовой плоскости. Для симметричных сечений косой изгиб невозможен.

11.3. Положение нейтральной оси и опасных точек

в поперечном сечении. Условие прочности при косом изгибе.

Определение размеров поперечного сечения.

Перемещения при косом изгибе

Положение нейтральной оси при косом изгибе определяется по формуле

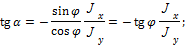
тогда

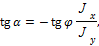
где 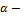угол наклона нейтральной оси к оси х;

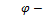угол наклона силовой плоскости к оси у (рис. 11.3).

В опасном сечении бруса (в заделке, рис. 11.3) напряжения в угловых точках определяются по формулам:

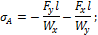
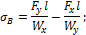
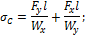
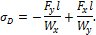
При косом изгибе, как и при пространственном, нейтральная ось делит сечение бруса на две зоны – зону растяжения и зону сжатия. Для прямоугольного сечения эти зоны показаны на рис. 11.4.

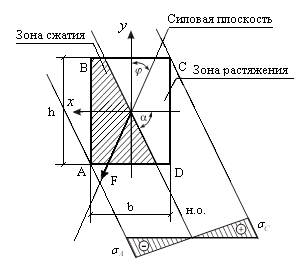
Рис. 11.4. Схема сечения защемленного бруса при косом изгибе

Для определения экстремальных растягивающих и сжимающих напряжений необходимо провести касательные к сечению в зонах растяжения и сжатия, параллельные нейтральной оси (рис. 11.4).

Наиболее удаленные от нейтральной оси точки касания А и С – опасные точки в зонах сжатия и растяжения соответственно.

Для пластичных материалов, когда расчетные сопротивления материала бруса при растяжении и сжатии равны между собой, т. е. [σ_р] = = [σ_c] = [σ], в опасном сечении определяется 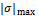и условие прочности можно представить в виде

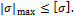
Для симметричных сечений (прямоугольник, двутавровое сечение) условие прочности имеет следующий вид:

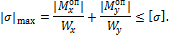
Из условия прочности вытекает три вида расчетов:

- проверочный;

- проектировочный – определение геометрических размеров сечения;

- определение несущей способности бруса (допускаемой нагрузки).

Если известно соотношение между сторонами поперечного сечения, например, для прямоугольника h = 2b, то из условия прочности защемленного бруса можно определить параметры b и h следующим образом:

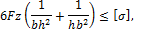
или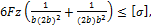

далее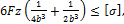

окончательно .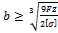

Аналогичным образом определяются параметры любого сечения. Полное перемещение сечения бруса при косом изгибе с учетом принципа независимости действия сил определяется, как геометрическая сумма перемещений в главных плоскостях.

Определим перемещение свободного конца бруса. Воспользуемся способом Верещагина. Вертикальное перемещение находим перемножением эпюр (рис. 11.5) по формуле

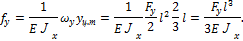
Аналогично определим горизонтальное перемещение:

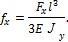
Тогда полное перемещение определим по формуле

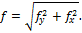
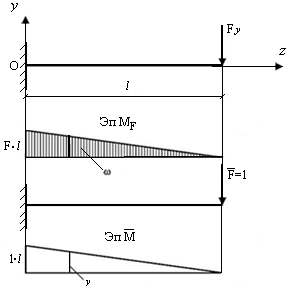
Рис. 11.5. Схема для определения полного перемещения

при косом изгибе

Направление полного перемещения определяется углом β (рис. 11.6):

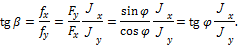
Полученная формула идентична формуле для определения положения нейтральной оси сечения бруса. Это позволяет сделать вывод, что 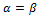, т. е. направление прогиба перпендикулярно нейтральной оси. Следовательно, плоскость прогибов не совпадает с плоскостью нагружения.

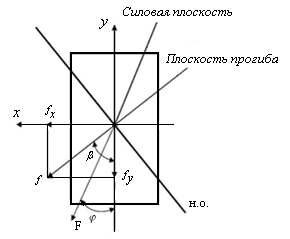
Рис. 11.6. Схема для определения плоскости прогиба

при косом изгибе

Угол отклонения плоскости прогиба 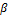от главной оси y будет тем большим, чем большим будет перемещение. Поэтому для бруса с упругим сечением, у которого отношение J_x/J_y велико, косой изгиб опасен, так как вызывает большие прогибы и напряжения в плоскости наименьшей жесткости. Для бруса, у которого J_x = J_y, суммарный прогиб лежит в силовой плоскости и косой изгиб невозможен.

11.4. Внецентренное растяжение и сжатие бруса. Нормальные

напряжения в поперечных сечениях бруса

Внецентренным растяжением (сжатием) называется такой вид деформации, при котором растягивающая (сжимающая) сила параллельна продольной оси бруса, но точка ее приложения не совпадает с центром тяжести поперечного сечения.

Такой тип задач часто применяется в строительстве при расчете колонн зданий. Рассмотрим внецентренное сжатие бруса. Обозначим координаты точки приложения силы F через х_F и у_F,а главные оси поперечного сечения – через х и у. Ось z направим таким образом, чтобы координаты х_F и у_F были положительными (рис. 11.7, а)

Если перенести силу F параллельно самой себе из точки С в центр тяжести сечения, то внецентренное сжатие можно представить как сумму трех простых деформаций: сжатия и изгиба в двух плоскостях (рис. 11.7, б). При этом имеем:

,

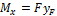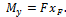
Напряжения в произвольной точке сечения при внецентренном сжатии, лежащей в первом квадранте, с координатами x и y можно найти исходя из принципа независимости действия сил:

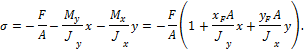
Так как

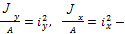квадраты радиусов инерции сечения, то

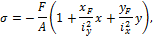
где x и y – координаты точки сечения, в которой определяется напряжение.

При определении напряжений необходимо учитывать знаки координат как точки приложения внешней силы, так и точки, где определяется напряжение.

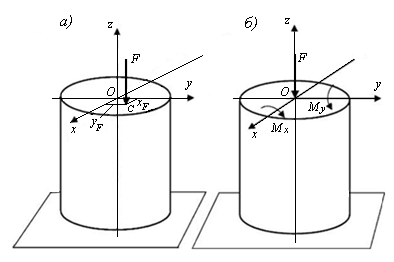Рис. 11.7. Схема бруса при внецентренном сжатии

В случае внецентренного растяжения бруса в полученной формуле следует заменить знак «минус» на знак «плюс».