Особенности расчета брусьев при сложном сопротивлении

Элементы конструкций и сооружений кроме простых деформаций (растяжение, сжатие, изгиб, сдвиг и кручение) могут испытывать более сложные деформации, такие как пространственный изгиб, косой изгиб, внецентренное растяжение (сжатие), изгиб с кручением и др. Такое сопротивление элементов конструкций называется сложным сопротивлением.

В расчетах жестких брусьев (стержней) на сложное сопротивление используется принцип независимости действия сил, который применим в случаях, когда деформации малы и подчиняются закону Гука.

Рассмотрим расчет прямых брусьев при сложном сопротивлении на примере пространственного изгиба. Такой вид деформации можно представить как изгиб в двух плоскостях, проходящих через ось бруса (рис. 11.1, а). При этом изогнутая ось бруса является пространственной кривой.

Для этого все внешние нагрузки следует разложить на составляющие, лежащие в главных плоскостях xOz и yOz, где оси у и x – главные оси инерции сечения (рис. 11.1, б).

В поперечных сечениях бруса возникают изгибающие моменты M_x, M_y и поперечные силы Q_x, Q_y. Действием поперечных сил пренебрегаем и учитываем только изгибающие моменты.

Напряжения в любой точке поперечного сечения бруса определяются по формуле

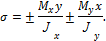
Знаки напряжений определяются знаками изгибающих моментов и координат точек сечения. Так как между напряжениями и координатами точек сечения существует линейная зависимость, то прямая, проходящая через начало координат, является геометрическим местом точек, в которых нормальные напряжения по сечению бруса равны нулю. Эта прямая называется нейтральной осью (рис. 11.2).

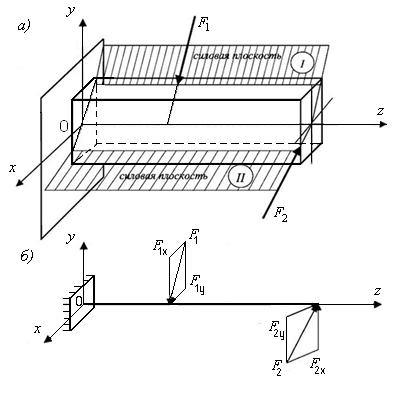
Рис. 11.1. Схема бруса, испытывающего пространственный изгиб

Уравнение нейтральной оси находим из уравнения для определения напряжений в поперечном сечении бруса, приравняв 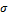нулю. Обозначив координаты точек нейтральной оси через у_о и х_о, получим:

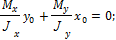
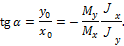
Согласно последней зависимости, нейтральная ось проходит через центр тяжести сечения. Положение нейтральной оси характеризуется ее углом наклона к оси х.

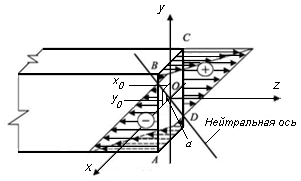
Рис. 11.2. Схема распределения нормальных напряжений

по сечению бруса при пространственном изгибе

Угол наклона нейтральной оси изменяется от сечения к сечению бруса в зависимости от изгибающих моментов М_х и М_у.

Для подбора размеров поперечного сечения бруса следует определить опасное сечение, в котором M_х и М_у одновременно достигают большого значения. Таких сечений может быть несколько. Затем в опасном сечении необходимо найти опасные точки – это наиболее удаленные от нейтральной оси точки (точки А и С на рис. 11.2), где у и х достигают максимального по абсолютной величине значения. Таким образом:

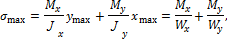
где 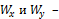моменты сопротивления сечения относительно соответствующих осей.

Для сечений, симметричных относительно обеих главных осей, напряжения в крайних точках сечения определяется по формуле

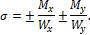
Условие прочности при пространственном изгибе:

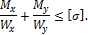
11.2. Косой изгиб, основные понятия. Нормальные напряжения