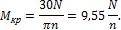Угол закручивания. Главные напряжения.

Потенциальная энергия упругой деформации при кручении

Из выражения крутящего момента при кручении определим относительный угол закручивания :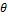

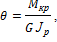
где

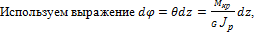проинтегрируем это выражение, если длина вала равна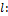

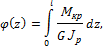
если 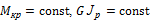, то решение интеграла принимает вид

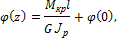
где 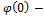угол закручивания сечения в начале системы отсчета.

Для определения касательных напряжений используем формулу 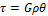. Подставляя в данную формулу выражение 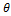, получим:

.

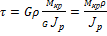Это уравнение показывает, что при чистом кручении в сечении вала возникают касательные напряжения, прямо пропорциональные крутящему моменту и радиусу, где они определяются, и обратно пропорциональные полярному моменту инерции.

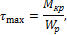
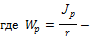полярный момент сопротивления вала.

При кручении внешние моменты, приложенные к валу, совершают работу вследствие поворота сечений, к которым они приложены. Эта работа расходуется на создание запаса потенциальной энергии деформации, численно равной работе внутренних сил.

Согласно закону Гука в пределах упругих деформаций угол закручивания растет пропорционально крутящему моменту. Поэтому зависимость крутящего момента от угла закручивания представляет собой прямую ОА, изображенную на рис. 10.6.

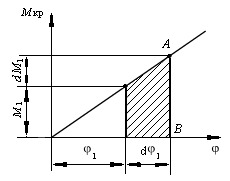
Рис. 10.6. Схема для определения потенциальной

энергии деформации при кручении

Пусть угол 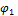соответствует промежуточному значению момента 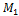. Увеличим момент на бесконечно малую величину 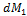. Тогда угол закручивания получит приращение .

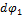Произведенная работа равна площади заштрихованной трапеции и находится по формуле

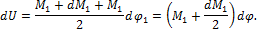
Тогда полная работа деформации при возрастании крутящего момента от 0 до М_кр равна накопленной потенциальной энергии и определяется площадью треугольника ОАB:

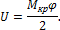
Подставим в полученную формулу значение угла закручивания, получим:

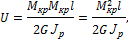
где G – модуль сдвига;

J_p– полярный момент инерции сечения;

l – длина вала.

Выразим потенциальную энергию через деформацию. В формулу для определения 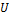подставим зависимость крутящего момента от угла закручивания, тогда:

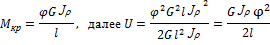
Расчет на прочность и жесткость круглого и кольцевого

Поперечного сечения. Расчет валов по заданной мощности

И частоте вращения

Произведем расчет валов на прочность и жесткость при кручении. Используя формулу для максимальных касательных напряжений, можем записать условие прочности при кручении в следующем виде:

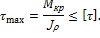
Из этого неравенства определяется полярный момент сопротивления:

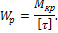
Для вала круглого поперечного сечения имеем:

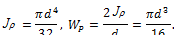
Подставим выражение 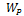в условие прочности при кручении и, решая данное уравнение относительно диаметра, получим следующую расчетную формулу:

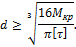
Расчетное значение диаметра округляем до ближайшего большего значения из ряда линейных размеров.

Если выбрать значение d несколько меньше расчетного диаметра, то необходимо выполнить проверочный расчет и убедиться, что перегрузка вала меньше 5 %, т. е. выполнить последовательно следующий расчет:

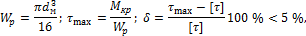
где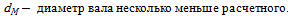

Из схемы распределения касательных напряжений (см. рис. 10.3) следует, что материал вала вблизи оси используется нерационально.
С точки зрения экономии металла и снижения веса конструкции следует выбирать вал пустотелый, поперечное сечение которого имеет форму кольца (рис. 10.7).

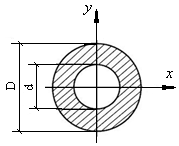
Рис. 10.7. Схема пустотелого вала

Обозначим через d внутренний диаметр кольца, D – наружный диаметр, α = d/D – отношение диаметров.

Определим геометрические характеристики кольцевого сечения вала:

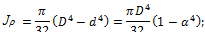
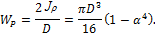
Из условия прочности при кручении определим значение D:

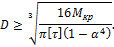
Расчетное значение D округляется до ближайших значений и 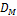, и затем выполняется проверочный расчет:

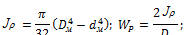
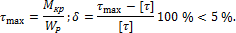
Условие жесткости вала представим в следующем виде:

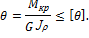
Значения 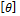зависит от условия работы вала и задается в градусах на длину вала. При статической нагрузке принимают:

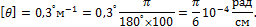
Если при проверочном расчете не выполняется условие прочности, то диаметр вала необходимо подбирать из условия жесткости:

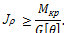
Для сплошного вала:

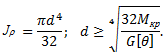
Для вала кольцевого сечения с заданным соотношением диаметров

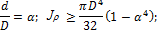
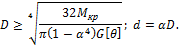
При расчетах валов на прочность, как правило, задают мощность N и число оборотов вала в минуту n. Мощность, передаваемая валом, определяется по формуле

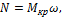
где 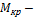крутящий момент в рассматриваемом сечении вала;

ω – угловая скорость вращения вала, рад/с.

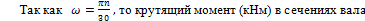определяется по формуле