Кручение прямого стержня круглого поперечного

Сечения. Напряжения в поперечном сечении вала.

Крутящий момент

Кручением называется такой вид деформации, при котором в поперечных сечениях элементов конструкций возникает только крутящий момент М_кр, а другие внутренние силовые факторы (продольная сила, изгибающие моменты, поперечные силы) равны нулю.

Сложность решения задачи по определению напряжений и деформаций при кручении зависит от формы поперечного сечения. Наиболее просто в механике материалов решаются задачи для стержней круглого и кольцевого поперечного сечения. Стержни круглого поперечного сечения, работающие на кручение, называются валами.

Чтобы определить напряжения в поперечных сечениях вала, рассмотрим уравнение, связывающее крутящий момент с касательными напряжениями:

,

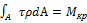где τ – касательное напряжение, действующее на элементарной площадке dА, расположенной на расстоянии ρ от центра тяжести сечения.

Так как закон распределения касательных напряжений по сечению вала не известен, то определить τ из интегрального уравнения невозможно. Для его определения рассмотрим деформации вала.

Для этого на поверхность круглого вала нанесем ортогональную сетку линий с постоянным шагом – прямые линии вдоль образующих цилиндра и окружности, перпендикулярные к продольной оси вала z (рис. 10.1, а). После деформации вала (рис. 10.1, б) образующие цилиндра переходят в винтовые линии, которые составляют угол γс образующими.

Все окружности в перпендикулярных сечениях сохраняют свою форму и поворачиваются одна относительно другой на некоторый угол, называемый углом закручивания. Длина вала не изменяется. Квадратные элементы на цилиндрической поверхности вала деформируются и приобретают форму ромбов.

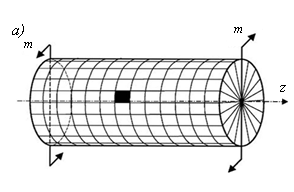
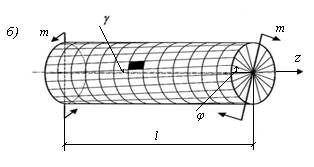
Рис. 10.1. Схема вала с ортогональной сеткой

на его поверхности

Допущения, основанные на гипотезе плоских сечений:

1) сечения, плоские до деформации, остаются плоскими после деформации и поворачиваются одно относительно другого на некоторый угол;

2) радиусы, проведенные мысленно в любом поперечном сечении, при кручении вала не искривляются.

Выделим часть вала длиной dz между двумя поперечными сечениями. Считаем, что правое сечение закреплено в заделке, а левое сечение закручивается моментом М_кр (рис. 10.2, б). При этом точка А остается неподвижной, а точка B переместится в положение 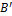. Мысленно вырежем в выделенном элементе внутреннюю часть с наружным радиусом ρ. Получим кольцевое сечение толщиной dρ. Определим значение 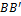из

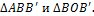
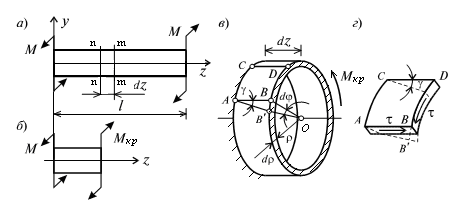Рис. 10.2. Схема выделенной части вала длиной dz

Из 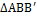имеем:

,

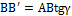учитывая, что при малых деформациях 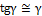, получим

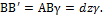
С другой стороны, из :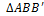

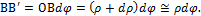
Окончательно получим:

,

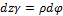откуда

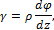
где 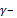угол сдвига,

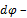абсолютный угол закручивания, размерность, рад.

Обозначим 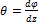– относительный угол закручивания, размерность, 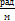, тогда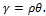

Используя закон Гука при сдвиге, получим:

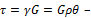величина касательных напряжений в сечении вала на расстоянии 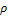от центра тяжести сечения; 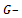модуль сдвига.

На основании полученной формулы можно сделать вывод, что 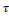в сечении вала распределяются по линейному закону и максимальные касательные напряжения 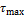возникают на поверхности вала. В центре вала касательные напряжения равны нулю.

Распределение касательных напряжений по сечению вала показано на рис. 10.3.

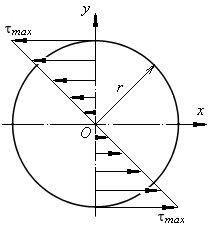
Рис. 10.3. Схема распределения касательных

напряжений по сечению вала

Величину крутящего момента M_кр можно определить через t. Момент относительно оси z от действия касательных напряжений t на элементарной площадке dА равен (рис. 10.4):

.

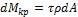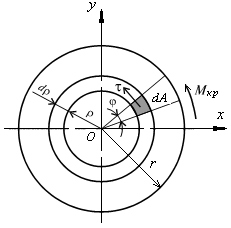
Рис. 10.4. Схема для определения М_кр

в сечении вала

Проинтегрировав это выражение по площади поперечного сечения вала, получим:

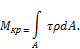
Пусть геометрические размеры поперечного сечения вала одинаковы по длине. Материал вала однороден и изотропен. Подставим в интеграл выражение , получим:

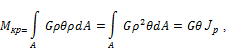
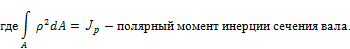
Правило знаков для крутящих моментов.

Если крутящий момент со стороны внешней нормали n к сечению вала вращается против часовой стрелки, то он считается положительным (рис. 10.5), в противном случае – крутящий момент считается отрицательным.

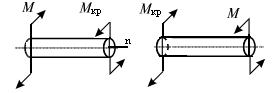
Рис. 10.5. Схема для определения знаков крутящих

моментов в сечениях вала

На эпюре крутящих моментов положительные значения откладываются вверх от нулевой линии, отрицательные значения – вниз.