Критерий удельной потенциальной энергии формоизменения

(четвертая теория прочности)

При построении этой теории первоначально была предложена гипотеза, согласно которой причиной наступления предельного состояния и разрушения считалась полная удельная потенциальная энергия, достигающая предельного значения. Условие прочности представляется в виде

где u – полная удельная энергия деформации, которая для объемного напряженного состояния имеет вид

[u] – простое предельное значение энергии, определяемое из опытов на напряжение.

Формула для вычисления [u] получается, если в предыдущем выражении положить т. е.

Тогда условие прочности запишется в виде

Однако эта гипотеза не прошла экспериментальную проверку и не нашла применения на практике, так как полученные на ее основе результаты не согласуются с экспериментом.

Поэтому была предложена новая теория, которая основана на гипотезе, согласно которой причиной наступления предельного состояния и разрушения считается часть удельной потенциальной энергии деформации, которая накапливается вследствие изменения формы элемента.

Поводом для этой гипотезы послужил тот экспериментальный факт, что при всестороннем сжатии разрушение практически не наступает. Таким образом, энергия, соответствующая изменению объема при всестороннем сжатии, не может служить критерием прочности.

Новая энергетическая теория связывается только с энергией формоизменения. Критерий прочности согласно этой теории представляется в виде

где удельная энергия формоизменения для рассматриваемого напряженного состояния;

допускаемая энергия формоизменения, полученная из опытов на простое растяжение.

Для вычисления удельной энергии формоизменения используем соотношение

где удельная энергия, затрачиваемая на изменение объема.

Представим заданное напряженное состояние (рис. 8.1, а), определяемое главными напряжениями в виде суммы двух напряженных состояний (рис. 8.1, б, в).

Рис. 8.1. Структурная схема объемного напряженного состояния

Первое соответствует гидростатическому растяжению (сжатию), когда по всем граням кубика действуют одинаковые напряжения:

Второе напряженное состояние характеризуется напряжениями

Изменение объема кубика от действия этих напряжений равно нулю. Действительно, подставляя их значение в формулу для объемной деформации, получим:

Тогда удельная энергия формоизменения определяется как разность между u и . После несложных преобразований получим:

Для случая простого растяжения получим:

.

Учитывая последнее равенство, согласно четвертой теории прочности:

Четвертая теория прочности хорошо подтверждается экспериментально для пластических материалов, одинаково работающих на растяжение и сжатие.

Теория прочности Мора

В отличие от изложенных выше теорий, теория Мора основывается не на гипотезах, а на экспериментальных данных. Зависимость между прочностными свойствами материала и видом напряженного состояния выводится и обосновывается с использованием кругов напряжений Мора. Для этого выбирается некоторое напряженное состояние, и одновременно увеличиваются его составляющие. Когда напряженное состояние станет предельным, на напряжениях и 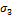строится соответствующий им круг Мора. Среднее напряжение не учитывается. Опыт показывает, что ошибка при этом не превышает 10–15 %. Строится ряд таких кругов, соответствующих различным напряженным состояниям (рис. 8.2). Огибающая этих кругов, форма которой зависит от свойств материала, является его механической характеристикой.

Если огибающая предельных кругов Мора построена, то для ответа на вопрос, является ли напряженное состояние, характеризующееся главными напряжениями , предельным, и для оценки прочности материала следует построить для и 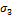круг напряжений в опасной точке материала. Прочность будет обеспечена, если он целиком лежит внутри огибающей. Для нахождения коэффициента запаса следует определить, во сколько раз необходимо увеличить и 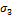, чтобы круг касался огибающей.

Для построения действительной огибающей предельных кругов Мора потребовалось бы опытным путем исследовать всевозможные напряженные состояния. Это неосуществимая задача, поэтому на практике действительную огибающую заменяют прямыми касательными лишь к двум предельным кругам, соответствующим опытам на одноосное растяжение и сжатие.

Рис. 8.2. Огибающая кругов Мора для различных напряженных

состояний материала

Условие прочности для промежуточного напряженного состояния с главными напряжениями и предельным кругом Мора с центром в точке О₃ (рис. 8.3) получим из следующих геометрических соотношений.

Проведем прямые О₁М₁, О₂М₂ и О₃ М₃,соединяющие центры предельных кругов Мора и точки их касания с предельной прямой, а также отрезок BО₁ параллельный М₁М₂. Из подобия ∆О₁О₂В и ∆О₁О₃А получим следующие зависимости:

где

Рис. 8.3. Схема для получения условия прочности Мора

Учитывая эти обозначения, преобразуем последнее равенство к виду:

Тогда получим условие прочности по теории Мора:

Если материал одинаково сопротивляется растяжению и сжатию, т. е. , теория прочности Мора совпадает с третьей теорией.

Выводы. Таким образом, разрушение материала может происходить путем отрыва одной части от другой и путем среза. Как правило, разрушение путем отрыва происходит хрупко, без заметных остаточных деформаций. Разрушение путем среза сопровождается пластическими деформациями. Поэтому первую и вторую теории можно применять для оценки прочности хрупких материалов, а третью и четвертую – пластических. Теория Мора позволяет учитывать разное сопротивление материала растяжению и сжатию.

Пример расчета

Задача 1. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.4). Проверить прочность детали по третьей теории прочности, если [σ] = 160 МПа.

Рис. 8.4. Схема опасной точки

нагруженной детали

Решение.

Задача 2. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.5). Проверить прочность материала по третьей и четвертой теориям прочности, если σ_р = σ_сж и [σ] = 160 МПа.

Рис. 8.5. Схема опасной точки

нагруженной детали

Решение.

.

Задача 3. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.6). Проверить прочность материала по четвертой теории прочности, если
[σ] = 90 МПа.

Решение.

Рис. 8.6. Схема опасной точки

нагруженной детали

8.8. Задачи для самостоятельного решения

Задача 4. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.7). Проверить прочность материала по четвертой теории прочности, если
σ_вр = 150 МПа, σ_всж = 300 МПа и [σ] = 100 МПа.

Рис. 8.7. Схема опасной точки

нагруженной детали

Ответ:

Задача 5. В опасной точке нагруженной детали напряженное состояние оказалось таким, как указано на схеме (рис. 8.8). Проверить прочность материала, если допускаемое напряжение [σ] = 150 МПа. Использовать третью и четвертую теории прочности.

Рис. 8.8. Схема опасной точки

нагруженной детали

Ответ: .

8.9. Контрольные вопросы

1. Какая точка тела называется опасной?

2. Что называется допускаемым напряженным состоянием?

3. Почему причина опасного состояния не имеет значения при расчетах на прочность при одноосном напряженном состоянии?

4. Что представляют собой теории прочности?

5. В чем сущность первой теории прочности?

6. В чем сущность второй теории прочности?

7. В чем сущность третьей теории прочности?

8. В чем сущность четвертой теории прочности?

9. В чем сущность теории Мора? В чем заключаются ее недостатки?

10. Область применения единой теории прочности.

ИЗГИБ