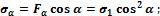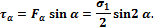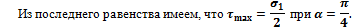Закон парности касательных напряжений

Параллелепипед под действием приложенных к нему сил (см. рис. 7.2) находится в равновесии, следовательно, должны соблюдаться уравнения статики. Составим сумму моментов всех сил, приложенных к граням параллелепипеда, относительно координатной оси z.

Из теоретической механики известно, что силы, пересекающие ось и параллельные ей, не создают момента относительно этой оси. Напряжения τ_ху и τ_ух, действующие на взаимно перпендикулярных гранях, создают моменты относительно оси z,равные по величине и противоположные по направлению. Поэтому соответствующее уравнение равновесия можно представить в следующем виде:

Откуда следует:

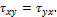
Аналогично составляя уравнения равновесия относительно других координатных осей

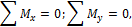
получим

Эти равенства называют законом парности касательных напряжений. Он гласит: на любых взаимно перпендикулярных площадках касательные напряжения равны по величине и направлены так, что стремятся вращать выделенный элемент в противоположные стороны.

Главные площадки и главные напряжения

При повороте выделенного элемента напряжения, действующие на его гранях, изменяются. При этом существуют такие площадки, на которых касательные напряжения равны нулю. Они называются главными площадками, а нормальные напряжения, действующие на этих площадках – главными напряжениями. Главные напряжения обозначают σ₁, σ₂ и σ₃, при этом индексы выбираются так, чтобы выполнялись алгебраические неравенства σ₁ > σ₂ > σ₃.

Если только одно главное напряжение отлично от нуля, то напряженное состояние называется одноосным или линейным, только два – двухосным или плоским, три – трехосным или объемным.

Линейное напряженное состояние

Рассмотрим стержень, растягиваемый силами N, действующими вдоль его оси. В поперечных сечениях стержня, достаточно удаленных от точек приложения сосредоточенных сил, нормальные напряжения распределяются равномерно и определяются по формуле (рис. 7.4, а):

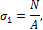
где 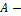площадь поперечного сечения.

Касательные напряжения в сечениях равны нулю. Следовательно, эти сечения являются главными площадками. Напряжения на площадках, параллельных оси стержня, равны нулю. Таким образом, стержень находится в линейном напряженном состоянии.

Определим напряжения на наклонных площадках. Проведем сечение стержня так, чтобы его внешняя нормаль составляла угол α с осью стержня. Будем считать угол α положительным, если он направлен против часовой стрелки. Действующие на наклонной площадке A_α напряжения: P_α = σ₁ – полное, σ_α – нормальное, τ_α – касательное (рис. 7.4).

Рис. 7.4. Схема линейного напряженного состояния

Составим уравнения равновесия отсеченной части стержня (рис. 7.4, б):

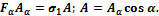
Откуда

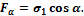
Проектируя 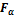на направление нормали и касательной к сечению, получим: