Теории напряженного и деформированного

СОСТОЯНИЙ

Напряженное состояние в точке. Виды напряженного

Состояния

Рассмотрим тело, находящееся в равновесии под действием пространственной системы сил. Внешние силы стремятся изменить взаимное расположение частиц тела, т. е. деформировать его. Внутренние силы (напряжения) стремятся воспрепятствовать этому.

В соответствии с гипотезой сплошности, материал в рассматриваемом теле распределяется непрерывно, а расположенная в данной точке частица взаимодействует с другими частицами. Поэтому напряжения распределяются непрерывно и в разных направлениях имеют различную величину.

Для исследования напряженного состояния тела выберем произвольную точку А и, используя метод сечений, выделим в ее окрестности элемент в виде параллелепипеда с гранями длиной dx, dy, dz, направленными вдоль координатных осей (рис. 7.1).

На гранях параллелепипеда действуют внутренние силы, заменяющие действие отброшенной части тела.

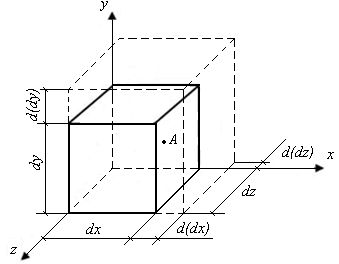
Рис. 7.1. Схема выделенного элемента

напряженного тела

B общем случае направление полных напряжений не совпадает с нормалью к площадке, на которой они действуют. Разложим их по трем взаимно перпендикулярным направлениям, совпадающим с координатными осями (рис. 7.2).

Напряжения, перпендикулярные к граням выделенного элемента, обозначаются символом σ с индексом, соответствующим координатной оси, вдоль которой они действуют, и называются нормальными. Два напряжения, расположенные на гранях выделенного элемента, обозначаются символом τ с двумя индексами, первый из которых соответствует координатной оси, перпендикулярной к площадке, второй – координатной оси, вдоль которой действует напряжение. Эти напряжения называются касательными. Так, например, на площадке, перпендикулярной к оси x, действуют напряжения σ_x, τ_xy, τ_xz (рис. 7.2).

Рис. 7.2. Схема распределения напряжений

на гранях параллелепипеда

Таким образом, на каждой грани выделенного элемента действуют три составляющие полного напряжения.

Правило знаков.

Нормальное напряжение считается положительным, если оно совпадает с направлением координатной оси, перпендикулярной к площадке, на которой это напряжение действует (растяжение), и отрицательным – наоборот (сжатие).

Знак касательных напряжений связан с направлением координатных осей.

Совокупность напряжений, действующих на трех взаимно перпендикулярных гранях, можно представить в виде матрицы, которая называется тензором напряжений:

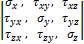
Если внешняя нормаль к площадке совпадает с направлением координатной оси, то на этой площадке касательное напряжение положительное, когда оно действует в направлении соответствующей оси.

Если же внешняя нормаль противоположна направлению оси, то касательное напряжение положительно, если оно действует в направлении, противоположном соответствующей координатной оси.

Таким образом, напряжения, возникающие на видимых гранях выделенного элемента (рис. 7.2), считаются положительными.

Напряженное состояние материала бывает линейным, плоским и объемным (рис. 7.3, а, б, в).

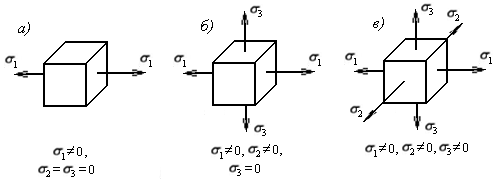
Рис. 7.3. Схема напряженных состояний материала