Заклепочных и болтовых соединений на срез и смятие.
Расчет сварных соединений
С теоретической точки зрения эти расчеты являются несовершенными, так как основываются на ряде упрощающих расчет допущений.
Расчет заклепочных и болтовых соединений. К числу таких допущений при расчете заклепочных соединений относится предположение, что в сечении, по которому может произойти разрушение от сдвига, касательные напряжения распределены равномерно. Предполагается также, что все заклепки (рис. 6.8) работают в одинаковых условиях и передаваемое усилие распределяется между заклепками равномерно, что при работе в упругой стадии материала практически невозможно.
Однако многолетняя служба различных сооружений показывает, что подобный расчет, несмотря на свой условный характер, вполне обеспечивает прочность конструкций.

Рис. 6.8. Схема заклепочного соединения
Заклепки для соединения элементов металлических конструкций начали применять в 20-е годы прошлого столетия. Так как заклепки изготавливаются из пластичных материалов, то разрушению предшествуют значительные деформации, что повышает надежность соединения.
В настоящее время заклепки применяются в основном в тяжелых конструкциях или при достаточно резких динамических нагрузках, которые испытывают соединяемые элементы конструкций.
Отверстия для заклепок в соединяемых деталях просверливаются, а в менее ответственных продавливаются.
Диаметр отверстия в деталях делается на 0,5–1,0 мм больше диаметра заклепки. Заклепка, имеющая с одной стороны головку, разогревается до определенной температуры (светло-красное каление) и вставляется в заготовленное отверстие. В некоторых соединениях используют холодные заклепки. Из выступающего конца стержня формируется вторая головка при помощи пневматического молотка или специальной клепальной машины. При этом стержень расширяется, плотно заполняет отверстие и при остывании сильно стягивает соединяемые детали. Таким образом, расчетным диаметром заклепки является диаметр заготовленного отверстия. Силы трения, возникающие на поверхности соединения элементов конструкций (листов), плотно сжатых заклепками, при расчете не учитываются, и принимается, что их взаимному скольжению препятствует только сопротивление заклепок срезу.
Заклепки в соединении внахлестку, изображенном на рис. 6.8, испытывают напряжения среза по одному поперечному сечению и называются односрезными заклепками. Разрушение от среза может произойти по сечениям т–п (рис. 6.9).

Рис. 6.9. Схема заклепки,
работающей на срез
Площадь среза одной заклепки определяется по формуле
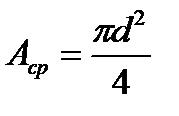 .
.
Если число заклепок в соединении равно n, то
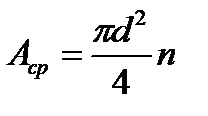 .
.
Соединение внахлестку имеет недостаток в том, что листы располагаются не в одной плоскости, вследствие чего силы F образуют пару сил, вызывающих изгиб листов и перекашивание соединения. Более рационально соединение листов впритык с накладками (рис. 6.10).
В таком соединении каждая заклепка испытывает напряжения среза по двум плоскостям. Такие заклепки называется двухсрезными заклепками.
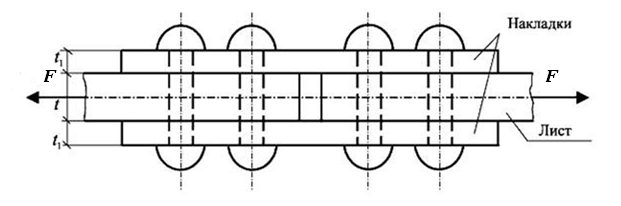
Рис. 6.10. Схема соединения листов впритык с помощью накладок
Встречаются конструкции, в которых склепываются целые пакеты листов (рис. 6.11). В таких случаях заклепки являются многосрезными.
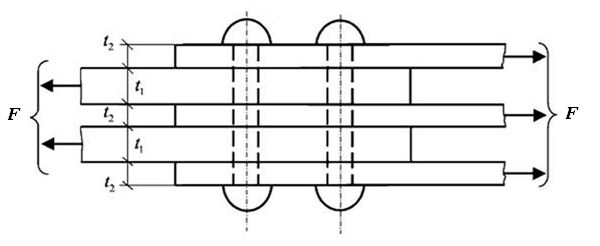
Рис. 6.11. Схема многосрезных заклепок при соединении пакета листов
Если число плоскостей среза обозначить через m, то площадь среза соединения определяется по формуле
 ,
,
где n – число заклепок, расположенных по одну сторону стыка.
Условие прочности соединения на срез имеет вид
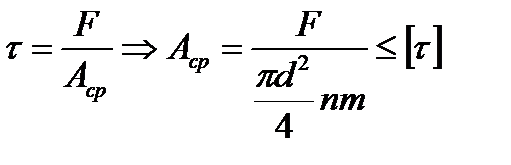 .
.
Данное условие позволяет выполнять три вида расчетов на прочность – проверочный, проектировочный и определение максимально допустимой нагрузки на соединение.
Проектировочный расчет обычно заключается в определении диаметра d заклепок, если их количество п задано конструктивно. Таким образом:
 .
.
Если конструктивно назначается диаметр заклепок d, то определяют их общее количество по формуле
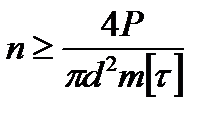 .
.
Количество срезов заклепки m определяется конструкцией соединения.
Деформация сдвига часто сопровождается смятием.
Смятием называется местная деформация сжатия, когда действие сжимающей силы передается на сравнительно небольшом участке. Если, например, соединить два деревянных бруса болтом, то при навинчивании гайки поверхность дерева под гайкой и головкой болта будет сжиматься, вдавливаясь внутрь древесины. В этих местах появится местное смятие, напряжение от которого быстро уменьшается по мере удаления от очага деформации. Для того чтобы уменьшить напряжение смятия дерева, увеличивают опорную поверхность в месте смятия, подкладывая под гайку и головку болта металлические шайбы, имеющие большую опорную поверхность с деревом.
В заклепочных и болтовых соединениях напряжения смятия распределяются неравномерно по полуцилиндрической поверхности отверстия листа и заклепки и имеют наибольшую величину в точке К (рис. 6.12, а).
Для упрощения расчетов условно принимают, что смятие происходит по площади тпрr.
Асм = td,
где d – диаметр заклепочного отверстия;
t – толщина листа.
Если заклепка соединяет два листа неодинаковой толщины, то в формулу следует подставить меньшую из них.
Для двухсрезных заклепок условной площадью смятия является:
Асм = td, или Асм = 2t1d.
В расчете принимают меньшую из этих двух величин.
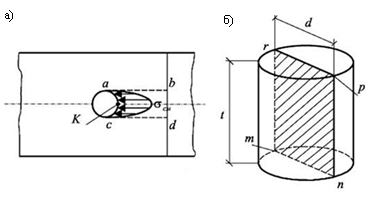
Рис. 6.12. Схема для расчета заклепки на смятие
Аналогично определяется площадь смятия и для многосрезных соединений. Так как предполагается, что напряжения смятия по условной площади распределяются равномерно, то условие прочности соединения на смятие принимает вид
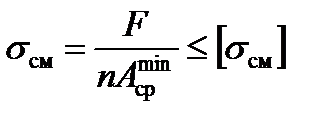 ,
,
где n – число заклепок;
[σсм] –допускаемое напряжение на смятие, для стали оно принимается [σсм] = (2 – 2,5)[σсм].
Расчет болтовых и заклепочных соединений на смятие проводится как проверочный.
Расчет сварных соединений. При изготовлении металлических конструкций часто применяется сварка с помощью электрической дуги, открытой русским ученым, профессором В. В. Петровым в 1802 году.
В настоящее время сварочное оборудование и технология сварки усовершенствованы и получили широкое распространение во всем мире. Немалая заслуга в развитии сварочного производства принадлежит академику Е. О. Патону.
Соединение элементов при помощи электросварки наиболее прогрессивно. Сварные соединения менее трудоемки, чем заклепочные, они не ослабляют сечений соединяемых элементов, упрощают конструкцию и по надежности не уступают заклепочным соединениям.
Наиболее простым типом сварного соединения является соединение встык, при котором зазор между двумя соединяемыми элементами заполняется наплавленным металлом. В зависимости от толщины соединяемых элементов зазорам между ними придают V-образную или X-образную форму. При малой толщине листов их кромки перед сваркой не обрабатываются (рис. 6.13).

Рис. 6.13. Схемы сварки элементов конструкций встык
Проверка сварного соединения на растяжение или сжатие производится из условия прочности
 ,
,
где [στ] – допускаемое напряжение при электросварке, зависит от вида сварки (ручная или автоматическая) и типа электродов (с тонкой или толстой обмазкой);
l – расчетная длина шва;
δ – толщина свариваемых элементов.
Сварное соединение элементов встык с косым швом (рис. 6.14), как показывают экспериментальные исследования, является равнопрочным целому сечению.

Рис. 6.14. Схемы сварки элементов конструкций встык косым швом
Другими типами соединения листов являются соединения внах-лестку, с накладными, в тавр и др., выполняемые при помощи валко-вых или угловых швов.
Угловой шов, параллельный направлению усилия, называется фланговым. Швы, перпендикулярные к действующему усилию, назы-ваются лобовыми, швы, идущие под углом к направлению силы, – косыми.
Расчет на прочность угловых швов производится условно на срез по сечению, расположенному в биссектронной плоскости прямого угла (рис. 6.15).
Площадь среза сварного шва (рис. 6.16) определим по формуле
Аср = δcos45о l = 0,7δl.
При расчете сварных швов на прочность предполагают, что касательные напряжения по плоскости среза распределяются равномерно. Из условия прочности можно определить расчетную длину сварного шва:
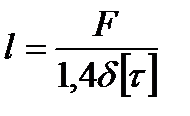 .
.
В некоторых элементах металлических конструкций растягивающая сила не проходит посредине привариваемой полки. Например, в уголке растягивающая сила проходит через центр тяжести сечения (рис. 6.17).

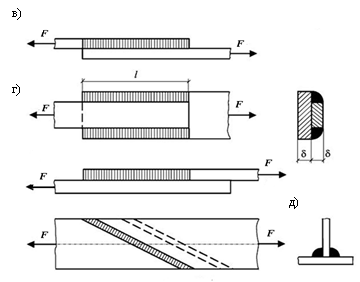
Рис. 6.15. Схемы сварки элементов конструкций внахлестку,
с накладками, тавром валковыми и угловыми швами
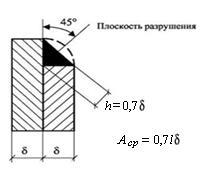
Рис. 6.16. Схема для расчета
площади среза сварного шва

Рис. 6.17. Схема для расчета длины швов
при приложении растягивающей силы
в центре тяжести привариваемого элемента
Усилия, приходящиеся на каждый шов, обратно пропорциональны расстояниям h1 и h2. Чтобы обеспечить одинаковые условия работы обоих швов, длина их должна быть разной и определяться из условия
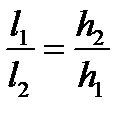 .
.
При одинаковой толщине шва условие прочности имеет вид:
 .
.
Из последних двух уравнений находится расчетная длина каждого шва.
Пример расчета
Задача 1.Элемент материала нагруженной детали (рис. 6.18) находится в состоянии чистого сдвига под действием касательных напряжений τ = 80 МПа. Проверить прочность детали по третьей теории прочности, если [σ] = 160 МПа.

Рис. 6.18. Схема площадки
нагруженной детали
Решение.
1. Определяем главные напряжения:
σ1 = τ = 80 МПа;
σ2 = 0;
σ3 = –τ = –80 МПа.
2. Определяем эквивалентное напряжение и проверяем прочность:
σэкв = σ1 – σ3 = 80 – (–80) = 160 МПа = [σ].
3. Прочность детали обеспечена. 
Задача 2. На гранях стального кубика (рис. 6.19) действуют касательные напряжения, под действием которых одна грань по отношению к другой сместилась на 0,25 мм. Проверить прочность кубика, если [τ] = 80 МПа, Е = 2 ´ 105 МПа, μ = 0,3.

Рис. 6.19. Схема стального кубика
Решение.
1. Определяем относительный сдвиг:
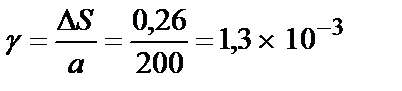 .
.
2. Определяем модуль сдвига:
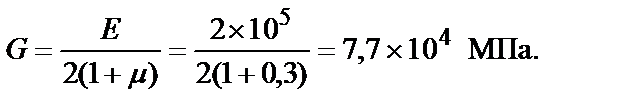
3. Определяем касательные напряжения и проверяем прочность:
τ = G × γ = 7,7 × 104 × 1,3 × 10–3 = 100 МПа = [τ].
Вывод: Прочность кубика обеспечена.
Задача 3. Стальной кубик с размерами ребер 100 мм находится в состоянии чистого сдвига. Касательные напряжения, действующие по граням кубика, τ = 120 МПа. Определить абсолютный и относительный сдвиг, а также модуль упругости при сдвиге G и удельную потенциальную энергию деформации, если модуль упругости при растяжении Е = 2 ´ 105 МПа, μ = 0,3.
Решение.
1. Модуль сдвига:
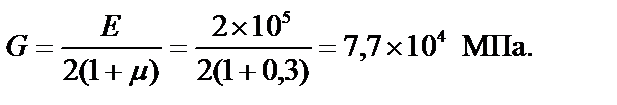
2. Относительный сдвиг:
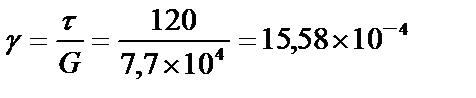 .
.
3. Абсолютный сдвиг:
∆S = γh = 15,58 × 10–4 × 0,1 = 1,558 × 10–4 м.
4. Потенциальная энергия деформации:
 .
.
Задача 4.Модуль упругости при растяжении хромоникелевой стали марки 20ХН Е = 2,15 × 105 МПа, коэффициент Пуассона μ = 0,28, [σ] = 180 МПа. Определить величину модуля упругости при сдвиге G и допускаемое напряжение на сдвиг для этой стали.
Решение.
1. Модуль сдвига:
 МПа.
МПа.
2. Допускаемое напряжение на сдвиг:
согласно третьей теории прочности:
[τ] = 0,5 [σ] = 0,5 × 180 = 90 МПа;
согласно четвертой теории прочности:
[τ] = 0,6 [σ] = 0,6 × 180 = 108 МПа.
Задача 5. Стальной параллелепипед нагружен силой F = 50 кН, как указано на схеме (рис. 6.20). Определить абсолютный и относительный сдвиг и проверить прочность, если [τ] = 80 МПа и G = 8 × 104 МПа.

Рис. 6.20. Схема стального
Параллелепипеда
Решение.
1. Элемент находится в условиях чистого сдвига. Площадь сдвига:
А = 5 × 2 = 10 см2 = 10 × 10–4 м2.
2. Напряжение:
 МПа < [τ].
МПа < [τ].
3. Относительный сдвиг:
 , γ = 6,25 × 10–4.
, γ = 6,25 × 10–4.
4. Абсолютный сдвиг:
∆S = h × γ = 80 × 6,25 × 10–4 = 0,05 мм;
∆S = 0,05 мм.
Задача 6. Для заданного напряженного состояния определить модуль сдвига материала (рис. 6.21), если относительный сдвиг площадок чистого сдвига γ = 14,5 × 10–4.

Рис. 6.21. Схема площадки материала
Решение.
1. σх = 100 МПа; σу = –100 МПа; τху = 60 МПа.
2. Определяем главные напряжения:

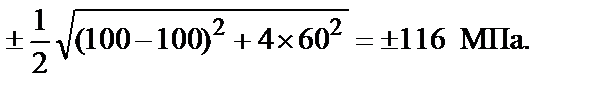
σ1 = 116 МПа; σ2 = 0; σ3 = –116 МПа.
3. Заданное напряженное состояние представляет собой чистый сдвиг под действием касательных напряжений τ = 116 МПа.
τ = 116 МПа.
τ = γG.
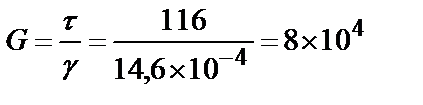 МПа.
МПа.
 МПа.
МПа.
6.7. Контрольные вопросы
1. Какой случай плоского напряженного состояния называется чистым сдвигом?
2. Зависимости между нормальными напряжениями по двум взаимно перпендикулярным площадкам при чистом сдвиге.
3. Изменяется ли значение полного напряжения при повороте площадки в случае чистого сдвига?
4. Как связаны друг с другом при чистом сдвиге значения σmax, σmin, τmax и τmin?
5. Как деформируется под действием касательных напряжений элементарный параллелепипед, боковые грани которого совпадают с площадками чистого сдвига?
6. Закон Гука при сдвиге.
7. Что называется абсолютным сдвигом, относительным сдвигом и углом сдвига?
8. Зависимость между модулем упругости E и модулем сдвига G.
9. Чему равна потенциальная энергия изменения объема при чистом сдвиге?
10. Расчет заклепочных соединений на срез и смятие.
11. Расчет сварных соединений внахлестку.
