При сдвиге. Закон Гука при сдвиге. Модуль сдвига

В сечении бруса между внешними силами F действует только поперечная сила Q,которая является равнодействующей касательных напряжений (рис. 6.2, б).

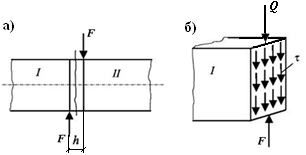
Рис. 6.2. Схема бруса для определения внутренних сил

и усилий при сдвиге

Так как расстояние между силами h очень мало, то действием изгибающего момента в сечении можно пренебречь.

Для определения напряжений при сдвиге применим метод сечений. Рассмотрим равновесие левой отсеченной части бруса. Воспользуемся интегральной зависимостью:

.

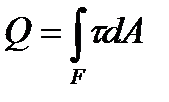Закон распределения касательных напряжений неизвестен. Если предположить, что они распределяются по сечению равномерно, то τ можно вынести за знак интеграла, тогда:

,

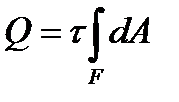следовательно,

.

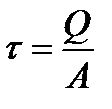На самом деле, касательные напряжения при сдвиге распределяются по сечению неравномерно, но для практических расчетов можно пользоваться вышеприведенной формулой.

Касательные напряжения в пределах упругих деформаций прямо пропорциональны относительной деформации сдвига, т. е.

Τ = Gγ.

Эта зависимость представляет закон Гука при сдвиге. Величина G характеризует способность материала сопротивляться сдвигу и называется модулем упругости второго рода, или модулем сдвига. Модуль сдвига G имеет размерность напряжения (т. е. МПа). Величина модуля упругости второго рода определяется экспериментально и для каждого материала имеет свое значение.

Вид диаграммы τ – γ при сдвиге для пластичной стали показан на рис. 6.3. Она напоминает аналогичную диаграмму σ – ε при растяжении.

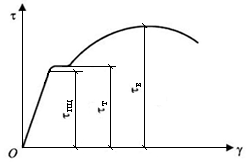
Рис. 6.3. Диаграмма напряженного состояния при сдвиге

Напряжение τ_пц (предел пропорциональности при сдвиге) является границей, до которой выполняется закон Гука.

Учитывая, что

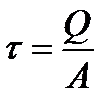и ,

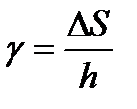находим абсолютную величину сдвига:

,

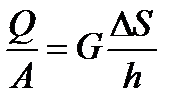откуда

.

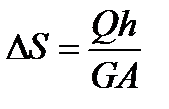Полученная формула аналогична зависимости для определения абсолютной деформации при растяжении:

,

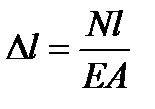где Е – модуль упругости первого рода (модуль Юнга).

6.3. Связь между модулями упругости E и G

Для изотропного тела

Установим зависимость между G и Е. Для этого на участке балки между приложенными внешними силами выделим элемент и рассмотрим его равновесие в процессе деформации (рис. 6.4).

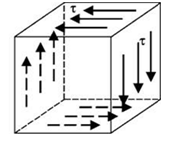
Рис. 6.4. Схема элементарного

параллелепипеда

На боковых вертикальных и горизонтальных гранях параллелепипеда действуют касательные напряжения. На гранях, параллельных плоскости чертежа, напряжения отсутствуют.

Деформация, при которой на гранях выделенного элемента возникают только касательные напряжения, называется чистым сдвигом.

При чистом сдвиге материал находится в плоском напряженном состоянии. При этом

.

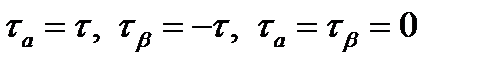Определим главные напряжения при чистом сдвиге и положения главных площадок.

Величины главных напряжений определяются по формулам:

;

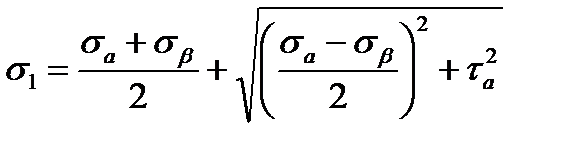σ₂ = 0;

.

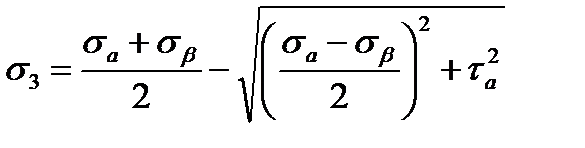Учитывая данные зависимости, получаем:

σ₁ = τ;

σ₂ = 0;

σ₃ = –τ.

Положение главных площадок определяется углом α:

.

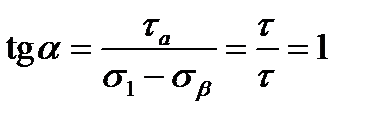Таким образом, при чистом сдвиге главные площадки наклонены к граням выделенного элемента под углом 45° (рис. 6.5, а).

Графическое определение направления главных напряжений σ₁ и σ₃ может быть получено с помощью круга Мора (рис. 6.5, б).

При деформации сдвигом прямые углы выделенного элемента бруса искажаются. При этом изменяются длины диагоналей.

Найдем удлинение диагонали квадратного элемента (рис. 6.6).

С одной стороны его можно объяснить деформацией сдвига. С другой – диагональ ВD можно представить как волокно материала, растягиваемое напряжением σ₁, и сжимаемое в поперечном направлении напряжением σ₃. Сказанное позволяет сделать вывод о том, что модули упругости G и Е не являются независимыми друг от друга величинами. Определим абсолютное удлинение диагонали ВD в процессе деформации:

.

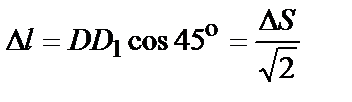Относительное удлинение диагонали ВD:

.

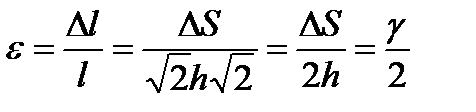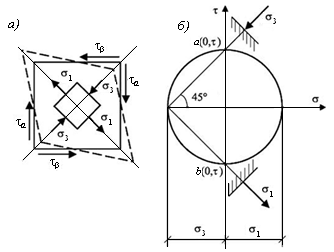
Рис. 6.5. Схема для определения положения главных площадок

при чистом сдвиге

По закону Гука для чистого сдвига

.

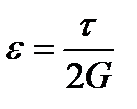Воспользуемся обобщенным законом Гука. Главное напряжение σ₁ действует в направлении диагонали BD₁. Таким образом, полученное значениеесть удлинение:

.

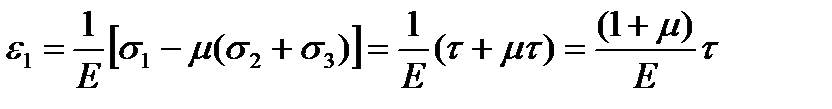Приравняв правые части выражений для определения, получим:

,

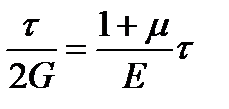или

.

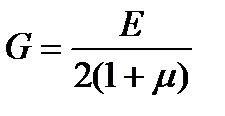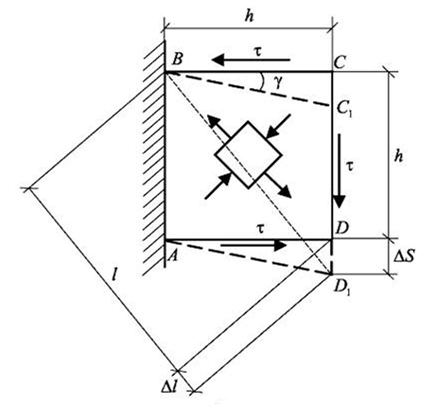
Рис. 6.6. Схема для определения связи между E и G

Данная формула устанавливает зависимость между тремя постоянными материала, характеризующими его упругие свойства, – модулями упругости первого и второго рода и коэффициентом Пуассона.

Например, для стали при Е = 2 × 10⁵ МПаи коэффициенте Пуассона μ = 0,25 находим

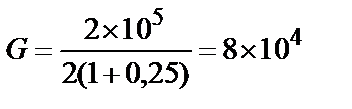МПа.

Чистый сдвиг имеет место в пластинках, нагруженных растягивающими нормальными напряжениями в одном направлении и сжимающими напряжениями в другом (рис. 6.7, а). По площадкам, расположенным под углом α = 45^о, действуют только касательные напряжения.

Приложение равномерно распределенных напряжений, как показано на рис. 6.7, а, трудно осуществить, поэтому состояние чистого сдвига обычно получают путем кручения цилиндрической трубы (рис. 6.7, б).

Вследствие малого поворота одного конца трубы относительно другого, элемент abсd, образованный двумя образующими и двумя смежными круговыми поперечными сечениями, подвергается чистому сдвигу.

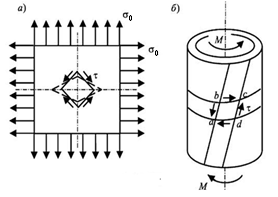
Рис. 6.7. Схема пластины и цилиндрической трубы,

которые подвергаются чистому сдвигу