Определение температурных напряжений
В статически неопределимых системах при изменении температуры возникают температурные напряжения (рис. 4.15).
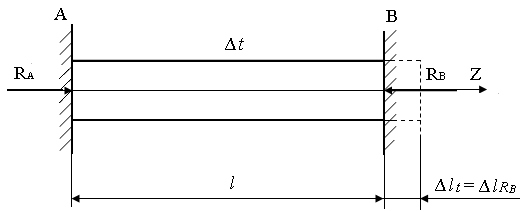
Рис. 4.15. Расчетная схема стержня при температурном воздействии
1. Составим уравнение равновесия: 
, 
·
2. Отбросим правую заделку, составим уравнение совместности деформаций:
·
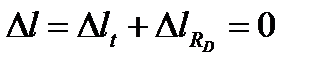отсюда по абсолютной величине
,
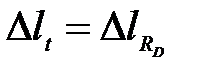где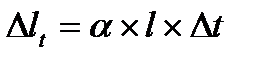 
;
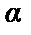– коэффициент линейного температурного расширения.
3. Согласно закону Гука имеем:
.
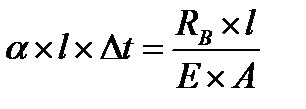Таким образом,
,
где А – площадь поперечного сечения стержня.
4. Определим температурные напряжения:
.
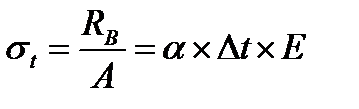Полученная формула справедлива лишь для определения напряжений в стержнях постоянного сечения с жесткой заделкой обоих концов.
Из этой формулы следует, что в статически неопределимых системах изменение температуры вызывает дополнительные напряжения. Они будут сжимающими при повышении температуры и растягивающими при понижении температуры. В статически определимых системах температурные напряжения не возникают. Для снятия температурных напряжений в практике широко применяются температурные швы и зазоры.
Задача 7. Стержень АВ состоит из двух соединенных между собой частей. Верхняя часть АС (рис. 4.16) – медная, имеет площадь поперечного сечения Ам = 25 см2, а нижняя СВ – стальная, имеет площадь поперечного сечения Аст = 12,5 см2. Между нижним концом стержня В и неподатливой опорой оставлен зазор Δ = 0,2 мм. Найти напряжения в обеих частях стержня при повышении температуры на Δt = 60 ○С и проверить его прочность, если [σ]м = 40 МПа, [σ]ст = 160 МПа.
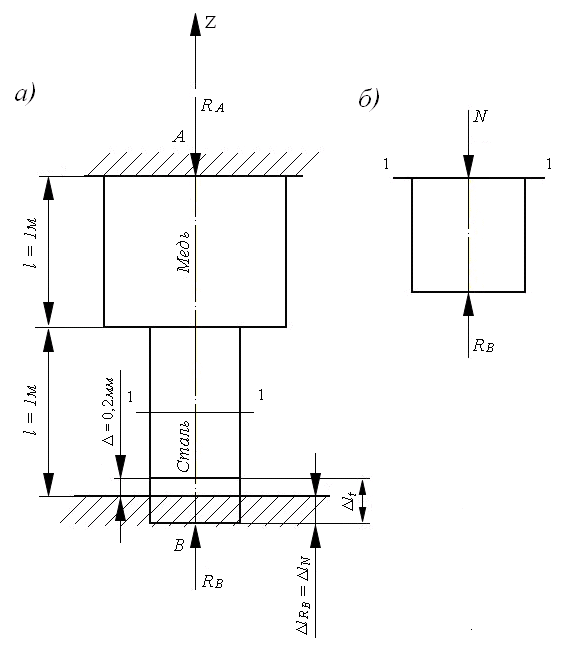
Рис. 4.16. а – схема составного стержня;
б – отсеченная нижняя часть стержня
Решение.
Определяем температурное удлинение составного стержня (рис. 4.16, а):
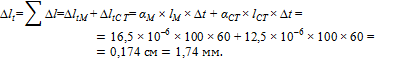
Так как Δ = 0,2 мм, то зазор между нижним концом стержня В и неподатливой опорой будет перекрыт и в опорах возникнут реакции.
2. Составим уравнение равновесия (рис. 4.16, а):
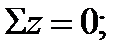
3. Составим уравнение совместности деформаций (рис. 4.16, а, б):
.
Отсюда
.
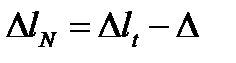4. Согласно закону Гука определим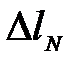 
для составного стержня:
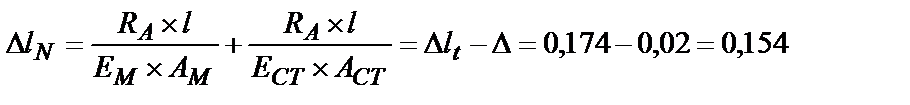см,
отсюда
5. Определим значения нормальных напряжений в сечениях составного стержня:
; 
.
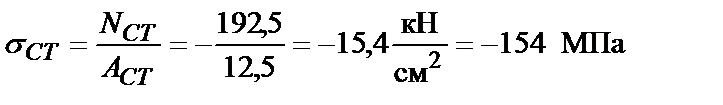6. 
> 
; 
< <
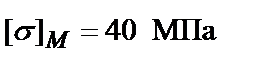Прочность составного стержня не обеспечивается.
Задача 8.Определить напряжения в стержнях жесткой невесомой балки (рис. 4.17, а) от температурного воздействия ∆t = 50 ºC на стержень 1.
Исходные данные: A1 = 6 см2, А2 = 10 см2, E1 = E2 = 2´104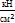 
, l1 = = 1,2 м, l2 = 1,5 м, а = 1 м, 
.
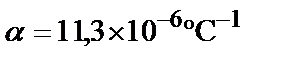Рис. 4.17. а – схема балки, подвергаемой температурному воздействию; б – расчетная схема для определения температурных напряжений в стержнях 1 и 2
Решение.
1. Определим деформацию стержня 1 от температурного воздействия:
.
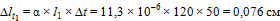2. Деформацию стержня 2 определим из выражения
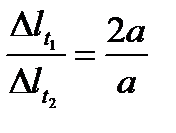, откуда 
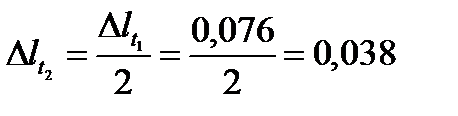см.
3. Определим нормальные усилия, возникающие в стержнях 1 и 2:
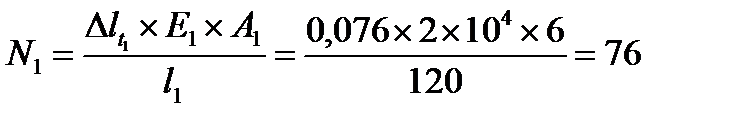кН;
кН.
4. Определим напряжения, возникающие в стержнях 1 и 2:
; 
.
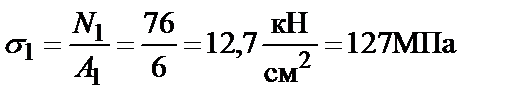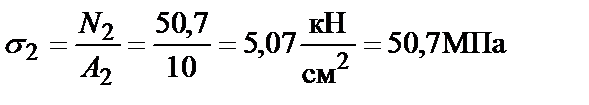4.8. Задачи для самостоятельного решения
Задача 9.Для заданной схемы нагружения бруса (рис. 4.18) построить эпюру нормальных сил и напряжений.
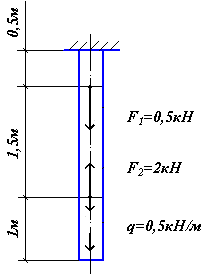
Рис. 4.18. Схема нагружения бруса
нормальными усилиями
Задача 10.Стальной ступенчатый стержень нагружен, как показано на рис. 4.19 Площади поперечных сечений соответственно равны: А1 = 8 см2; А2 = 5 см2; А3 = 2см2. Проверить прочность и жесткость стержня, если [σ] = 160МПаи [Δl] = 3мм.
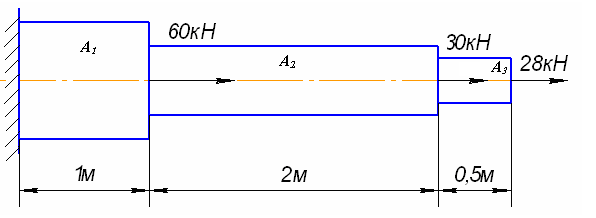
Рис. 4.19. Схема нагружения ступенчатого бруса
Задача 11.Определить, какой должна быть площадь поперечного сечения A деревянной колонны (сосна), длиной l = 2 м, сжимаемой силой F = 30 кН, чтобы опускание верхнего конца колонны не превышало 3 мм (рис. 4.20). Допускаемое напряжение [σ] = 10 МПа, Е = 104 МПа.
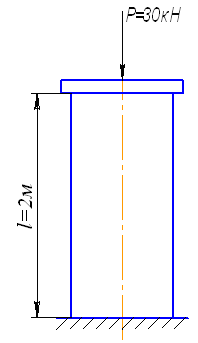
Рис. 4.20. Схема нагружения
деревянной колонны
Ответ: A = 30 см2.
Задача 12.Определить наибольшее значение допускаемой силы F для ступенчатого бруса, если [σ]р = 40 кПа, [σ]cж = 120 кПа. Площадь поперечного сечения соответственно равна А = 10 см2, А1 = 2А (рис. 4.21).
Рис. 4.21. Схема нагружения бруса
Ответ: [F] = 53 кН.
Задача 13.Жесткий стержень ВС, шарнирно прикрепленный к стене в точке В, опирается на стойку 1 и поддерживается стержнем 2 (рис. 4.22). Определить допускаемую нагрузку F, если стойка и стержень стальные и имеют одинаковую площадь поперечного сечения A = 20 см2. Допускаемое напряжение [σ] = 160 МПа.
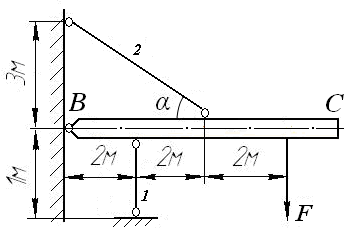
Рис. 4.22. Схема нагружения стержня
Ответ: [F] = 30 кН.
Задача 14.Медный круглый стержень вставлен в стальную трубу (рис. 4.23). Длина медного стержня больше длины стальной трубы на Δ = 0,05 мм. Какая должна быть приложена к жесткой плите нагрузка, чтобы после сжатия стержня и трубы в их сечениях возникли напряжения сжатия одинаковой величины, если их площади сечений одинаковы и равны А = 40 см2.
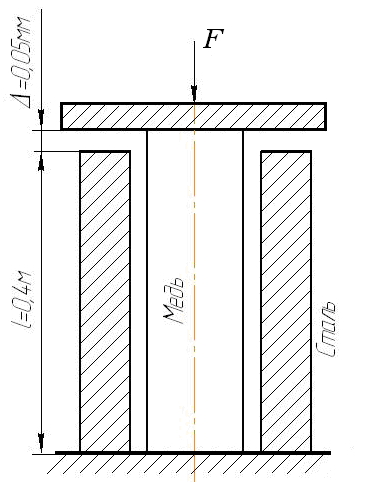
Рис. 4.23. Схема нагружения стержня
Ответ: F = 500 кН.
Задача 15.Определить усилия в четырех ножках стола, изображенного на рис. 4.24. Крышку стола и пол считать абсолютно твердыми.
Рис. 4.24. Схема нагружения стола
Ответ: N1 = 16,5 Н, N2 = N4= 27,5 Н, N3= 38,5 Н.
4.9. Контрольные вопросы
1. Что такое растяжение (сжатие) бруса (стержня) при осевом действии внешней нагрузки?
2. Какие внутренние силовые факторы возникают при центральном растяжении (сжатии)?
3. Как формулируется закон Гука, какова область его применения при осевом растяжении (сжатии) бруса?
4. Что такое напряжения и деформации при осевом растяжении (сжатии)? Как они определяются?
5. Что такое модуль упругости первого рода и коэффициент Пуассона при осевом растяжении (сжатии)? От чего они зависят?
6. Как построить эпюры нормальных усилий, напряжений и перемещений характерных сечений бруса при одноосном растяжении (сжатии)?
7. Как формулируются условия прочности и жесткости при растяжении (сжатии) бруса?
8. Какие виды расчетов вытекают из условий прочности и жесткости одностержневых систем при растяжении (сжатии)?
9. Потенциальная энергия упругой деформации. Как она определяется при одноосном растяжении (сжатии) бруса?
10. Какие системы называются статически неопределимыми при растяжении (сжатии)? Виды этих систем.
11. Как осуществляется расчет статически неопределимых одностержневых и многостержневых систем при действии на них температурных нагрузок и технологических неточностей?
12. В чем заключается особенность расчета напряжений и деформаций при учете собственного веса системы?