По специальностям 15.02.01, 21.02.03, 21.02.02, 18.02.09
МАТЕМАТИКА
методические указания
и варианты контрольных работ
для студентов заочного обучения
Курса
По специальностям 15.02.01, 21.02.03, 21.02.02, 18.02.09
Л.В. Габзалилова. Математика. Методические указания и варианты контрольных работ для студентов з/о по специальностям: 130502, 140206, 140101, 150411, 140613, 220301, 240404, 270111, 080110
Уфа: УТЭК 2010 стр. 35
Методические указания по курсу «Математика» содержит решения типовых задач с необходимым теоретическим материалом, 20 вариантов контрольной работы по 7 заданий в каждом, список рекомендуемой литературы
Рецензенты: Г.В. Сухарева – преподаватель УТЭК
ГАПОУ Уфимский топливно - энергетический колледж
Габзалилова Л.В. 2010
Введение
Данные методические указания составлены в соответствии с рабочей программой по дисциплине «Математика» и предназначены для студентов заочного обучения 1-го курса по всем специальностям.
В процессе изучения дисциплины математика студенты 1-го курса заочного обучения по специальностям 140206, 140101, 140613,270111, 080110 должны знать:
- основные понятия и методы линейной алгебры, приближенных вычислений, дифференциальные и интегральные исчисления, дифференциальных уравнений и комплексных чисел.
По специальностям 15.02.01, 21.02.03, 21.02.02, 18.02.09
должны знать:
- основные понятия и методы линейной алгебры, дифференциального и интегрального исчислений, дифференциальных уравнений; понятия теории множеств, теории графов, комбинаторики и теории вероятности.
Должны уметь:
употреблять математическую символику при решений задач, решать основные типовые задачи по перечисленным выше элементам линейной алгебры, математического анализа, дискретной математики и теории вероятностей. Все перечисленные выше знания, умения и навыки приобретаются слушателями в процессе самостоятельной работы и обязательных аудиторных занятий.
Основная литература
1. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах. Учебное пособие для СПО. М., Новая волна, 2012 г., 436 с.
2. Богомолов Н.В. Практические занятия по математике: учеб. пособие для СПО. – М.: Высшая школа, 2012-495 с.
Дополнительная литература:
1. Данько П.Е. Высшая математика в упражнениях и задачах. Часть 1 и 2. – М.: Высшая школа, 2012., 247 с.
2. Письменный Д. Конспект лекций по высшей математике 1-2 части Учеб. Пособие Издание второе, исправленное. – М.: Айрис-пресс, 2013. – 570 с.
Указание к выполнению и оформлению контрольных работ
1. Студенты выполняют контрольную работу в соответствии с учебным планом в сроки, установленные колледжем. Контрольная работа состоит из 7 заданий по одному из каждой темы.
2. Контрольная работа выполняется в отдельной тетради в клеточку, аккуратно, разборчивым почерком. Чертежи выполняются простым карандашом с использованием инструментов.
3. На заключительном листе контрольной работы следует указать список литературы, которым пользовались.
4. На титульном листе указать фамилию, имя, отчество, специальность студента, группу, номер варианта контрольной работы.
5. Решения задач располагать в порядке номеров, указанных в заданиях, сохраняя номера задач.
6. Перед решением каждой задачи надо выписать полностью ее условие. Решение задач следует излагать подробно и аккуратно, комментируя все действия по ходу решения, и делая необходимые чертежи.
7. После получения проверочной работы, как незачтенной, так и зачтенной, студент должен исследовать все отмеченные проверочные ошибки и недочеты и выполнить указанные исправления заданий.
После исследования всех указанных ошибок или дополнений, нужно прислать работу для повторной проверки с незачтенными работами.
Без контрольной работы зачет и экзамен не принимается!
Выбор задания определяется в соответствии с последней цифрой своего шифра, так как в каждой теме 10 вариантов заданий. Из каждой темы выбирается задание по последней цифре своего шифра. Например, шифр студента 256. Значит, из первой темы он выбирает задание под номером 6, из второй темы – под номером 16, из третьей – под номером 26, из четвертой – под номером 36 и т.д. все семь заданий.
Темы контрольной работы
Для специальностей 15.02.01, 21.02.03, 21.02.02, 18.02.09
1. Элементы теории множеств (№ 1-10)
2. Решение линейных систем уравнений методом Крамера и Гаусса (№ 11-20)
3. Элементы комбинаторики (№ 21-30)
4. Дифференциальное исчисление (№ 31-40)
5. Интегральное исчисление (№ 41-50)
6. Дифференциальные уравнения (№ 51-60)
7. Элементы теории графов (№ 61-70)
Темы контрольной работы
Для специальностей 15.02.01, 21.02.03, 21.02.02, 18.02.09
Тема 2. Решение линейных систем уравнений методами
а) Крамера, б) Гаусса
№ 11-20
11.
а) 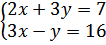 б)
б) 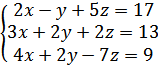
12.
а) 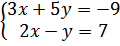 б)
б) 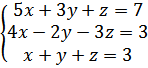
13.
а) 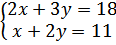
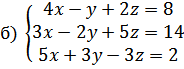
14.
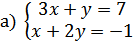 б)
б) 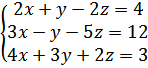
15.
а) 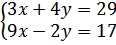 б)
б) 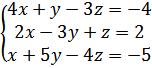
16.
a) 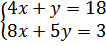
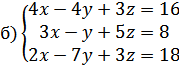
17.
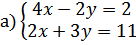 б)
б) 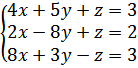
18.
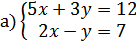 б)
б) 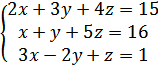
19.
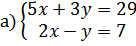 б)
б) 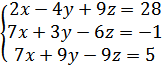
20.
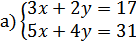
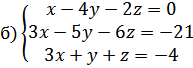
Тема 3. Элементы комбинаторики. [6], гл 5, п 1-3
№ 21-30.
21. Решить уравнение: 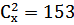
22. Решить уравнение: 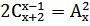
23. Сколько способов распределения 3 одинаковых путевок в дом отдыха среди 5 рабочих цехов?
24. Сколько способов распределения путевок в санаторий , дом отдыха и в турбазу среди 5 рабочих цехов?
25. Решить уравнение: 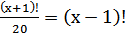
26. Сколько способов расставить 10 различных книг на полке?
27. Сколько трехзначных чисел можно образовать из цифр 2;8;7 без повторных цифр?
28. Сколько двухзначных чисел можно образовать из цифр 2;8;7 без повторных цифр?
29. Сколько четырехзначных чисел можно образовать из цифр 1;2;3;4 без повторных цифр?
30. Сколькими способами можно распределить 12 человек по бригадам по 6 человек в каждом?
Тема 4. Дифференциальное исчисление [1], гл. 7,8 § 1,2 [3], § 20,24
№ 31-40. Найти:
а) Производную и дифференциал функции
б) Наибольшее и наименьшее значение на [а;b]
31. a) 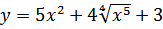
б) 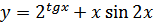
в) 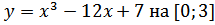
32. a) 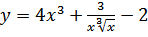
б) 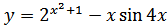
в) 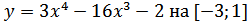
33. a) 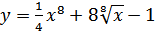
б) 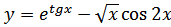
в) 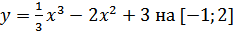
34. a) 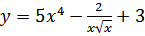
б) 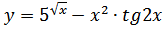
в) 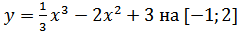
35. a) 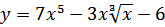
б) 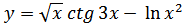
в) 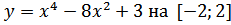
36. a) 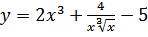
б) 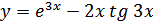
в) 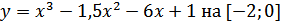
37. a) 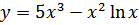
б) 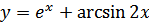
в) 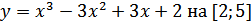
38. a) 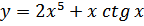
б) 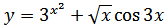
в) 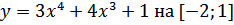
39. a) 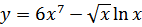
б) 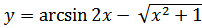
в) 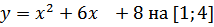
40. a) 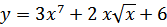
б) 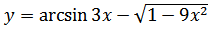
в) 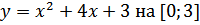
Тема 5. Интегральное исчисление [3] гл. 9,10 § 1,2 [1] гл. 10,11 § 1,2
№ 41-50. Найти интегралы в п. а), б), в) и площадь фигуры, ограниченный линиями в п. г)
41. a) 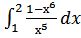
б 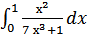 )
)
в) 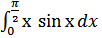
г) 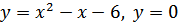
42. a) 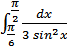
б) 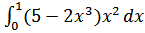
в) 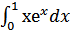
г) 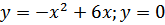
43. a) 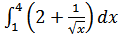
б) 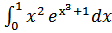
 в)
в) 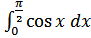
г) y= 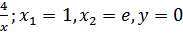
44. а) 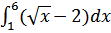
б) 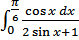
в) 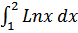
г) 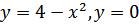
45. а) 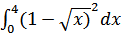
б) 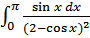
в) 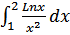
г)y= 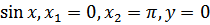
46. а) 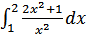
б) 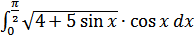
в) 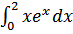
г) 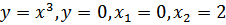
47. а) 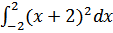
б) 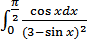
в) 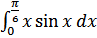
г) 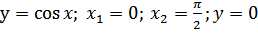
48. а) 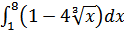
б) 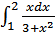
в) 
г) 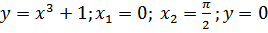
49. а) 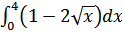
б) 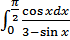
в) 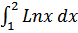
г) 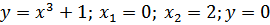
50. а) 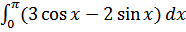
б) 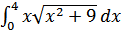
в) 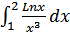
г) 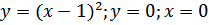
Тема 6. Дифференциальные уравнения [1], гл.12 § 1, 2
№ 51-60
Найти решение дифференциальных уравнений
а) общее,
б) частное
51.
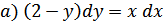 ; б)
; б) 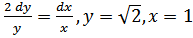
52.
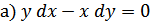 ; б)
; б) 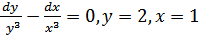
53.
а) 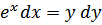 ;
; 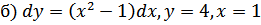
54.
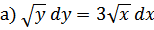 ;
; 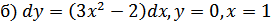
55.
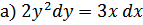 ;
; 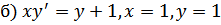
56.
а) 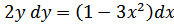 ;
; 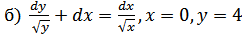
57.
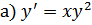 ;
; 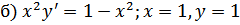
58.
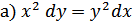 ;
; 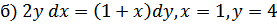
59.
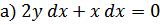 ;
; 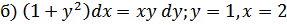
60.
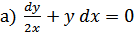 ;
; 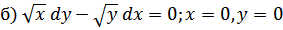
Тема 7. Элементы теории графов. [6], гл 4, п 1-4
№ 61-70. Для графа найти:
а) множество вершин, дуг и ребер, вид графа.
б) матрицу смежности вершин.
в) матрицу ребер и вершин.
г) маршруты длины 2.
| b |
| a |
61. 62.
| c |
| d |
65. 1 2 66. 1 2
3 4 4 3
67. 1 2 68. 1 2
4 3 3 4
69. 1 2 70. A b
4 3 d с
Примеры решений типовых заданий
Основные логические символы
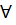 хР(х) – квантор общности (означает “для любого х выполняется
хР(х) – квантор общности (означает “для любого х выполняется
Р (х)”.)
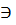 хР(х) – квантор существования (означает “существует х, для которого выполняется Р (х)”.)
хР(х) – квантор существования (означает “существует х, для которого выполняется Р (х)”.)
Р ⇒ Q – импликация (“из Р следует Q ”)
⟺ - эквивалентность (“тогда и только тогда”)
Р ∧ Q – конъюнкция ( “Р и Q”)
Р ∨ Q – дизъюнкция (“Р или Q”)
Не Р или - отрицание Р
: = - символы присвоения (“положим”)
def – (“положим по определению”)
Используя эти символы можно записать:
1) (А = В) ⟺(( 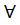 х ∈ А ⇒ х ∈ В) ∧ (
х ∈ А ⇒ х ∈ В) ∧ ( 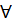 х ∈ В ⇒ х ∈ А)
х ∈ В ⇒ х ∈ А)
2) (А ⊆ В) ⟺ (  х/х ∈А ⇒ х ∈ В)
х/х ∈А ⇒ х ∈ В)
3) ( А = В) ⟺ ( В ⊂ А ∧ А⊂ В)
∩
Задание множеств
Перечислением элементов: М: = { а1; а2; а3; …; аn }
или характеристическим свойством Р(х)
(предикатом): М: = { х | Р(х) }
Например:
1) В = { х ∈ N | х < 3} означает, что В= { 1; 2}
2) А ={ х ∈ N | х +1=5} означает, что А = {4}
3) В = { х ∈ N | х M5} или {5;10;15…}
т.е. { х | Р(х) }означает, что множество элементов х множества обладает свойством Р(х)
4) М = { х ∈ N | х 3< 5}={1;2;3;4;5;6;7}
Операции над множествами
Рассматриваются следующие операции над множествами:
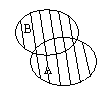
10. Объединение множеств А и В.
 U
U
А ∪ В = { х/х ∈ А или х ∈ В} – т.е. состоит из элементов, принадлежащих хотя б одному из множеств А или В.
20. Пересечение множеств А и В.
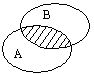 A∩B = {x/x ∈ A и x ∈ B} – т.е. состоят из элементов, принадлежащих одновременно А и В.
A∩B = {x/x ∈ A и x ∈ B} – т.е. состоят из элементов, принадлежащих одновременно А и В.
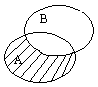
3º. Разность множеств А и В.
 U
U
A/B = {x/x ∈ A и x ∉ B} – т.е. состоит из элементов А, не принадлежащих В.
4º. Симметрическая разность А и В (или кольцевая сумма А и В)
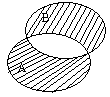 А Ө B = {x/x ∈ A и x ∉ B} ∪ {x/x ∈ В и x ∉ А} или {А\В ∪ В\А}
А Ө B = {x/x ∈ A и x ∉ B} ∪ {x/x ∈ В и x ∉ А} или {А\В ∪ В\А}
5º. Дополнение А до универсума
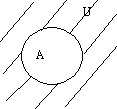
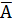 = U\A = {x|x ∈ Uux и x ∉ А}
= U\A = {x|x ∈ Uux и x ∉ А}
Произведение множеств
Прямым (декартовым) произведением двух множеств А и В называется множество всех упорядоченных пар, в которой I элемент из множества А, II элемент – из множества В, т.е. А×В = {(а, в)/а Є А ̂в Є В}
Пример: А={2;5;7;9} и В ={2;4;7},
Тогда А×В = {(2,2) ; (2,4) ; (2,7) ; (5,2) ; (5,4) ; (5,7) ; (7,2) ; (7,4) ; (7,7) ; (9,2) ; (9,4 ); (9,7)}
А∩В={2,7}; А∪В={2,4,5,7,9}; А/В={5,9}; В/А={4}; А Ө В={4,5,9}
Элементы множества А×В называются точками; В паре (х, у) абсцисса – х и ордината – у точки, соответствующей этой паре.
Множество точек плоскости является прямым произведением вида R×R=R2, где R–множество действительных чисел.
R2 называется декартовым квадратом на R.
Элементы теории графов. Виды и способы задания графов
Во многих прикладных задачах изучаются системы связей между различными объектами. Объекты называются вершинами и обозначаются точками, а связи – дугами. Такие системы образуют графы. Например: граф изображает сеть улиц а городе; сеть дорог, трубопроводов, блок – схемы программирования и многие другие модели.
Определение. Графом называется совокупность двух множеств – непустого множества V вершин и множество Е двухэлементных подмножеств множества V (множество ребер Е).
Обозначаются G(V,E) = <V;E>,V≠O
Множество двух элементных подмножеств определяет симметричное бинарное отношение на множестве Е = V×V, E = E-1; поэтому ребро можно считать не только как множество 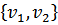 , но и как пару
, но и как пару 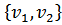 число вершин обозначают Р, число ребер – q; если дугами являются пары вершин
число вершин обозначают Р, число ребер – q; если дугами являются пары вершин 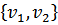 то дуга считается исходящей из v1 и заходящей в v2; граф G изображают диаграммой.
то дуга считается исходящей из v1 и заходящей в v2; граф G изображают диаграммой.
2
1 V = 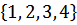 - множество вершин
- множество вершин
3 Е = 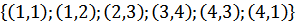 -
-
Множество дуг
Если имеется несколько дуг, исходящих из вершины v1 в вершину v2 , такие дуги называются кратными, граф называется кратным.
Если все элементы множества Е – упорядоченные пары, то граф G называется ориентированным (орграф), элементы V называются узлами, а множество Е дугами, т.е. если 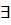 (а, b)
(а, b) 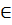 E, (b, a) ∉ E
E, (b, a) ∉ E
Если элементом Е может быть пара одинаковых (не различных) элементов V, то такой элемент называется петлей, а граф называется графом с петлями (псевдографом). Если Е содержит несколько одинаковых элементов, то эти элементы называются кратными ребрами, a G - мультиграфом.
Если 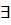 (а, b)
(а, b) 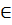 E /\ (b, a)
E /\ (b, a) 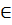 E, то G называется неориентированным (неографом). В этом случае дуга называется ребром и обозначается в виде отрезка, соединяющего вершины, а вершины а и b называются концами ребра
E, то G называется неориентированным (неографом). В этом случае дуга называется ребром и обозначается в виде отрезка, соединяющего вершины, а вершины а и b называются концами ребра 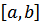 и информацию об этих дугах пишут:
и информацию об этих дугах пишут: 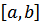 =
= 
 или
или 
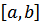 - ребро графа
- ребро графа
Матрица смежности вершин
Матрица инциденций вершин отражает смежность вершин.
Пример 1.
а1 а2
G: а5
а3 а4
AG=(Ai, j) = 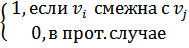 ; AG=
; AG= 
Для мультиграфа G матрица инцидентности дуг и вершин
BG=(Bi, j) = 
Это – матрица размера m×n, I = 1,2…,m
J = 1,2,…,n
Пример 2.
a2 4 a3
3
1 2
a1
BG= 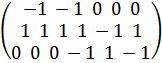
m×n3×6 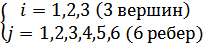
Тема: Комбинаторика
1. Размещения из n элементов по m это - упорядоченные подмножества из n элементов по m.
Число размещений 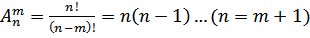
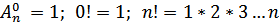 (n-факториал)
(n-факториал)
2. Перестановки - размещение и n элементов по n т.е. частный случай размещений число перестановок Pn=n!
3. Сочетания – подмножество из п элементов по m, отличающихся друг от друга хотя бы одним элементом называются сочетаниями. Число сочетаний 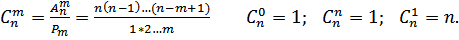
Пример:
1. Сколькими способами можно расположить 5 различных книг на полке? Р5=1*2*3*4*5=120 способов.
2. Сколько способов распределить 3 различных путевки среди 8 человек бригады?
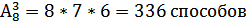
3. Сколько способов распределить 3 одинаковых обязанностей в группе из 25 человек?
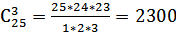 способов т.к. обязанности одинаковы – это сочетания
способов т.к. обязанности одинаковы – это сочетания
Тема 4. Дифференцирование
а) Найти экстремумы функции
б) наибольшее и наименьшее значение функции [-1;3]
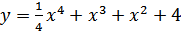
Решение.
1. Найти y|: y|=x3+3x2+2x;
y|=0;
x3+x2+2x=0;
x(x2+3x+2)=0; т.е. x1=-1; x2=0; x3=-2 – критические точки.
2. Найти y|| : y||=3x2+6x+2
Найти значение y|| при критических точках
ymin (-2)=4; т.к. y||=(-2)>0 т.е. функция имеет min;
ymax(-1)=17/4;т.к. y||=(-1)<0 т.е. функция имеет max;
ymin (0)=4; т.к. y||=(0)>0 т.е. функция имеет min;
б) Для нахождения наибольшего или наименьшего значения находят критические точки, принадлежащие отрезку [-1;3], значения f(x) при этих критических точках и на концах отрезка; среди найденных значений выбирают f наибольшее и f наименьшее.
1. y|= x3+3x2+2x=0;
| Î[-1;3] |
x2=-1
Найдем 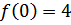
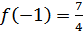
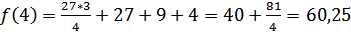
f наибольшее (3)=60,25
f наименьшее (0)= 4
Примеры решения по теме 5: Интегральные исчисления
а) Вычислить 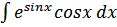
Данный интеграл вычисляется методом замены переменной.
Решение:
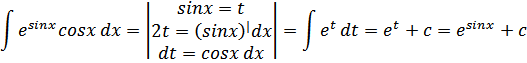
Проведем дифференцирование:
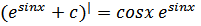 – подынтегральная функция
– подынтегральная функция
б) Вычислить 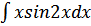
Решение: интеграл вычисляется по частям: 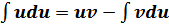
r w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 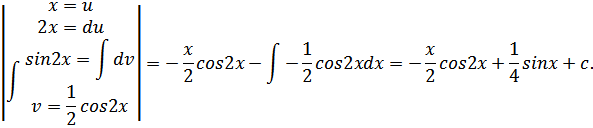
Аналогично можно проверить. Что произведение полученной функции равно подынтегральной функции, т.е интеграл вычислен правильно.
в) Вычислить 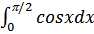
Решение.
При вычислении переделенного интеграла используются такие же методы что и неопределенного. Но затем пользуются формулой Ньютона- Лейбница:
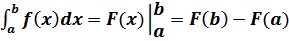
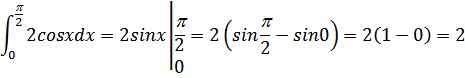
г) Найти площадь фигуры : у=х2-2х – парабола с вершиной в точке (1;-1), ветви вверх точка пересечения с осью ОХ : (0;0); (2;0)
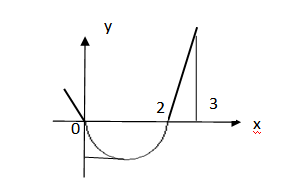
s=s1+s2;
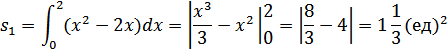
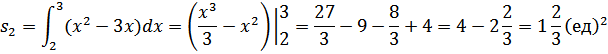
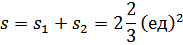
Тема: Комплексные числа. Алгебраическая форма комплексного числа a+bi; {a,b}ªR, i- мнимая единица, i2=-1
Сложение:
z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i
(2+3i)+(5-7i)=(2+5)+(3-7)i=7-4i
Вычитание:
z1-z2 =(a+bi)-(c+di)=(a-c)+(b-d)i
(5+4i)-(2-3i)=(5-2)+(4+3)i=3+7i
Умножение:
z1*z2=(a+bi)*(c+di)=(ac-bd)+(ad+bc)i
(a+bi) на (c+di) умножаем по правилам действий над многочленами.
(1+2i)(3-i)=3*1-1*i+6i-2i2=3+2-i+6i=5+5i
Деление: на практике при делении комплексных чисел удобно домножить числитель и знаменатель дроби на выражении, сопряженное знаменателю:
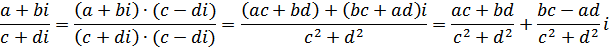
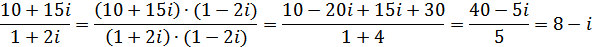
Возведение в степень мнимой единицы:
i1=i;
i2=-1;
i3=i2*i=-1*i=-i;
i4=i2 *i2=(-1)(-1)=1;
i5=i3*i2=-i(-1)=i;
i6=i5*i=i*i=-1=i2;…
Видим закономерность:
i(4n+r)=(i4)n*ir=(1)n*ir=ir
Получаем:
i4m=1;
i4m+1=i;
i4m+2=-1;
i4m+3=-i;
i218=i4*54+2=i2=-1.
Сумма и произведение двух сопряженных комплексных чисел являются действительными числами:
z+z=(a+bi)+(a-bi)=2a;
z*z=(a+bi)(a-bi)=a2+b2.
Каждому комплексному числу z=a+bi можно поставить в соответствие точку M(a;b) координатной плоской, абсцисса которой равна действительной части комплексной части комплексного числа, а ордината - мнимой части. (рис. )
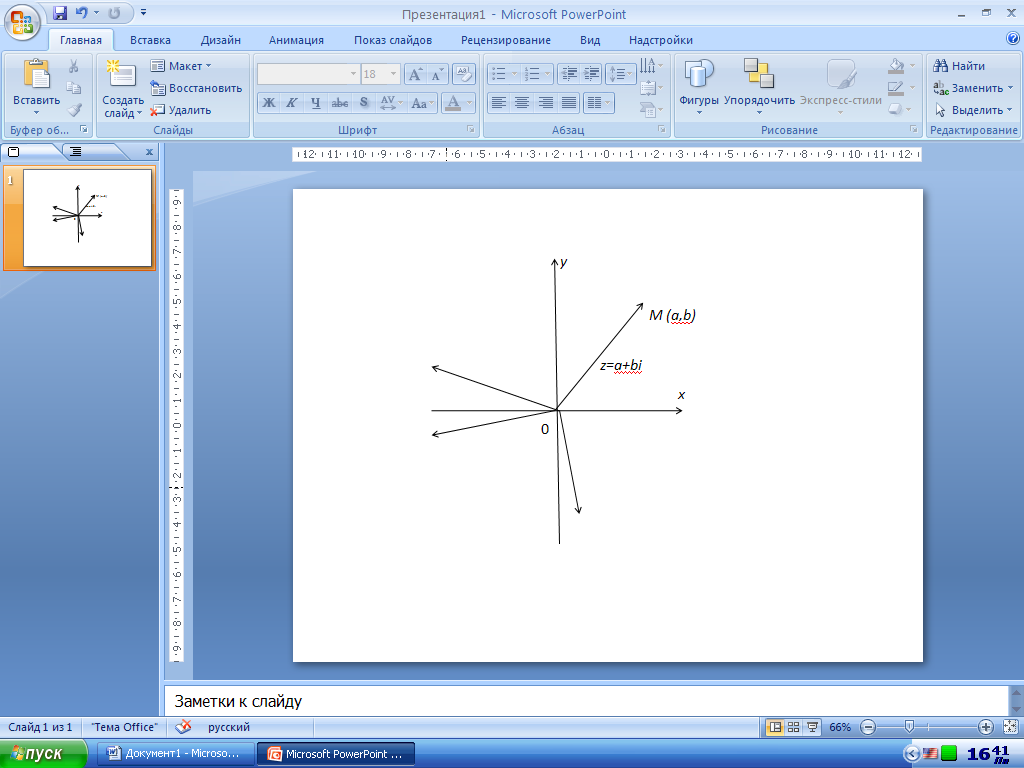
Рис.
Важной и удобной является интерпретация комплексного числа a+bi как радиус - вектора OM, т.е. вектора, исходящего из начала координат O(0,0) и идущего в точку M(a;b). Разумеется , вместо радиус вектора OM можно взять любой равный ему вектор. Изображение комплексных чисел с помощью векторов удобно тем, что при этом получают простое геометрическое истолкование операций над ними . При сложении чисел z1=a+bi и z2=c+di складываются их действительные и мнимые части . При сложении соответствующих им векторов OM1 и OM2 складываются их координаты:
числу z1+z2 соответствует вектор OM1+OM2,
числу z1-z2 – вектор OM1 – OM2.
Модулем комплексного числа z1=a+bi называется арифметический квадратный корень из суммы квадратов его действительной части и коэффициента при мнимой единице:
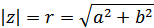
Аргументом комплексного числа z1=a+bi называется радианная мера угла φ, образованного этим вектором с положительным направлением действительной оси 0≤φ<2π,
arg z=φ
Величина угла считается положительной, если отсчет ведется против часовой стрелки и отрицательной, если отсчет производится по часовой стрелке.
Возьмем на плоскости точку М(a,b), пусть ей соответствует комплексное число z1=a+bi. Обозначим через φ угол, который образует радиус – вектор OM с положительным направлением оси OX.
Тригонометрическая форма комплексного числа r(cosφ+ isinφ), показательная форма reφi
Действия в показательной форме:
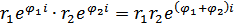
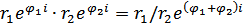
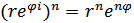 - формула Муавра.
- формула Муавра.
Аналогично в тригонометрической форме:
Пример.
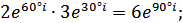
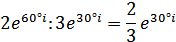
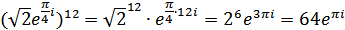
МАТЕМАТИКА
методические указания
и варианты контрольных работ
для студентов заочного обучения
Курса
по специальностям 15.02.01, 21.02.03, 21.02.02, 18.02.09
Л.В. Габзалилова. Математика. Методические указания и варианты контрольных работ для студентов з/о по специальностям: 130502, 140206, 140101, 150411, 140613, 220301, 240404, 270111, 080110
Уфа: УТЭК 2010 стр. 35
Методические указания по курсу «Математика» содержит решения типовых задач с необходимым теоретическим материалом, 20 вариантов контрольной работы по 7 заданий в каждом, список рекомендуемой литературы
Рецензенты: Г.В. Сухарева – преподаватель УТЭК
ГАПОУ Уфимский топливно - энергетический колледж
Габзалилова Л.В. 2010
Введение
Данные методические указания составлены в соответствии с рабочей программой по дисциплине «Математика» и предназначены для студентов заочного обучения 1-го курса по всем специальностям.
В процессе изучения дисциплины математика студенты 1-го курса заочного обучения по специальностям 140206, 140101, 140613,270111, 080110 должны знать:
- основные понятия и методы линейной алгебры, приближенных вычислений, дифференциальные и интегральные исчисления, дифференциальных уравнений и комплексных чисел.
По специальностям 15.02.01, 21.02.03, 21.02.02, 18.02.09
должны знать:
- основные понятия и методы линейной алгебры, дифференциального и интегрального исчислений, дифференциальных уравнений; понятия теории множеств, теории графов, комбинаторики и теории вероятности.
Должны уметь:
употреблять математическую символику при решений задач, решать основные типовые задачи по перечисленным выше элементам линейной алгебры, математического анализа, дискретной математики и теории вероятностей. Все перечисленные выше знания, умения и навыки приобретаются слушателями в процессе самостоятельной работы и обязательных аудиторных занятий.
Основная литература
1. Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика в 2-х томах. Учебное пособие для СПО. М., Новая волна, 2012 г., 436 с.
2. Богомолов Н.В. Практические занятия по математике: учеб. пособие для СПО. – М.: Высшая школа, 2012-495 с.
Дополнительная литература:
1. Данько П.Е. Высшая математика в упражнениях и задачах. Часть 1 и 2. – М.: Высшая школа, 2012., 247 с.
2. Письменный Д. Конспект лекций по высшей математике 1-2 части Учеб. Пособие Издание второе, исправленное. – М.: Айрис-пресс, 2013. – 570 с.
Указание к выполнению и оформлению контрольных работ
1. Студенты выполняют контрольную работу в соответствии с учебным планом в сроки, установленные колледжем. Контрольная работа состоит из 7 заданий по одному из каждой темы.
2. Контрольная работа выполняется в отдельной тетради в клеточку, аккуратно, разборчивым почерком. Чертежи выполняются простым карандашом с использованием инструментов.
3. На заключительном листе контрольной работы следует указать список литературы, которым пользовались.
4. На титульном листе указать фамилию, имя, отчество, специальность студента, группу, номер варианта контрольной работы.
5. Решения задач располагать в порядке номеров, указанных в заданиях, сохраняя номера задач.
6. Перед решением каждой задачи надо выписать полностью ее условие. Решение задач следует излагать подробно и аккуратно, комментируя все действия по ходу решения, и делая необходимые чертежи.
7. После получения проверочной работы, как незачтенной, так и зачтенной, студент должен исследовать все отмеченные проверочные ошибки и недочеты и выполнить указанные исправления заданий.
После исследования всех указанных ошибок или дополнений, нужно прислать работу для повторной проверки с незачтенными работами.
Без контрольной работы зачет и экзамен не принимается!
Выбор задания определяется в соответствии с последней цифрой своего шифра, так как в каждой теме 10 вариантов заданий. Из каждой темы выбирается задание по последней цифре своего шифра. Например, шифр студента 256. Значит, из первой темы он выбирает задание под номером 6, из второй темы – под номером 16, из третьей – под номером 26, из четвертой – под номером 36 и т.д. все семь заданий.
Темы контрольной работы
