Вопрос 24. Перестановка из n элементов.

Пусть имеется n различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

Pn=n!=1⋅2⋅3⋅...⋅(n−1)⋅nPn=n!=1⋅2⋅3⋅...⋅(n−1)⋅n

Символ n! называется факториалом и обозначает произведение всех целых чисел от 11 до n. По определению, считают, что 0!=1,1!=10!=1,1!=1.

Вопрос 25. Размещения из n элементов по m элементам.

Пусть имеется n различных объектов. Будем выбирать из них m объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по m, а их число равно

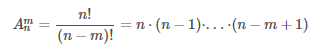
Пример всех размещений из n=3n=3 объектов (различных фигур) по m=2m=2 - на картинке справа. Согласно формуле, их должно быть ровно A23=3⋅(3−2+1)=3⋅2=6A32=3⋅(3−2+1)=3⋅2=6.

Вопрос 26. Сочетания из n элементов по m элементам.

Пусть имеется n различных объектов. Будем выбирать из них m объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниямииз nn объектов по mm, а их число равно

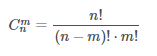
Пример всех сочетаний из n=3 объектов (различных фигур) по m=2- на картинке справа. Согласно формуле, их должно быть ровно 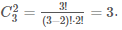. Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний - нет), причем именно в m! раз, то есть верна формула связи:

Вопрос 27. Правило суммы и произведения.

Большинство комбинаторных задач решается с помощью двух основных правил - правила суммы и правила произведения.

Правило суммы. Если некоторый объект 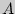можно выбрать 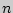способами, а другой объект 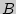можно выбрать 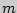способами, то выбор "либо 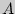, либо 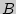" можно осуществить 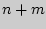способами.

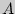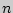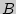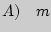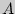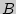Правило произведения. Если объект можно выбрать способами, а после каждого такого выбора другой объект можно выбрать (независимо от выбора объекта способами, то пары объектов и можно выбрать способами.

Пример. Наряд студентки состоит из блузки, юбки и туфель. Девушка имеет в своем гардеробе четыре блузки, пять юбок и трое туфель. Сколько нарядов может иметь студентка?

Решение. Пусть сначала студентка выбирает блузку. Этот выбор может быть совершен четырьмя способами, так как студентка имеет четыре блузки, затем пятью способами произойдет выбор юбки и тремя способами выбор туфель. По принципу умножения получается 4*5*3=60 нарядов (комбинаций).

Вопрос 28. Основные понятия теории вероятностей.

Испытанием в теории вероятностей называют какой-нибудь эксперимент (не обязательно научный). Например, подбросили монетку — испытание. Вытянули лотерейный билет — испытание. Провели жеребьёвку спортивного соревнования — тоже испытание.

Если есть эксперимент, есть и возможные результаты — то, чем он может закончиться. Список возможных результатов можно составлять по-разному, но стандартный способ — выбрать максимальное дробление результатов. Например, при бросании кубика можно сказать, что есть два результата: {выпало 66} и {выпало не 66}, — но это не очень удобно, так как второй результат можно раздробить на более мелкие. Составляя список возможных результатов, мы должны также помнить, что два результата никогда не могут случиться одновременно (условие взаимоисключения).

Испытанием называется эксперимент с очерченным набором возможных взаимоисключающих результатов. Эти результаты называются исходами.

Случайное событие — это подмножество множества исходов испытания.

Любое случайное событие может состоять из одного или нескольких исходов испытания (тогда это событие возможно) или не содержать ни одного исхода (невозможное событие). Например, "выпало больше 77" — невозможное событие для испытания "бросание кубика". Отдельно определяют достоверное событие, то есть такое, которое включает в себя все исходы данного испытания.

Исходы, входящие в событие, называются благоприятными для этого события.

Итак, пусть у нас есть испытание с определённым набором равновозможных исходов. Вероятностью некоторого случайного события называется отношение количества благоприятных исходов к общему количеству исходов испытания.