Тема: «Традиционный подход к решению задач методом наименьших квадратов».

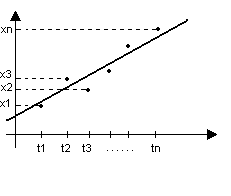
Пусть заданы экспериментальные значения х₁,х₂,…,х_n полученные в моменты времени t₁,t₂,...,t_n

Задан класс функций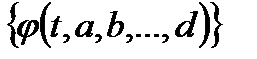

Каждая функция, из указанного класса, определяется значениями параметров a, b, …, d.

Например, в качестве класса функций могут выступать класс квадратных трехчленов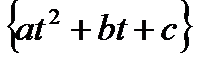

Задача состоит в том, чтобы найти функцию 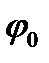, такую что

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

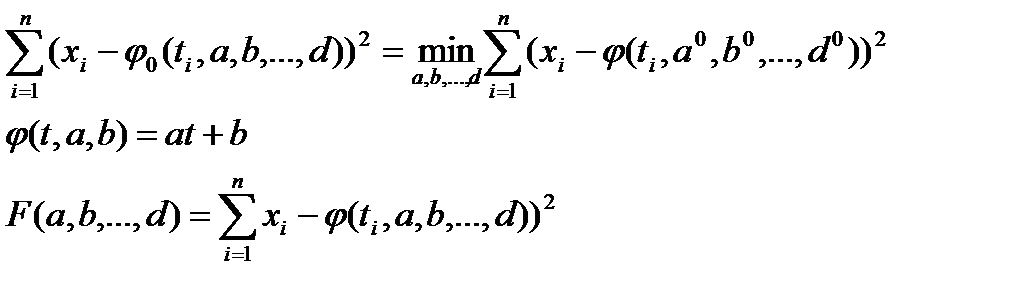
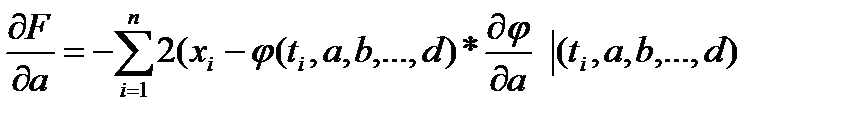
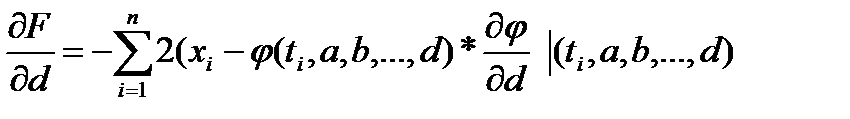
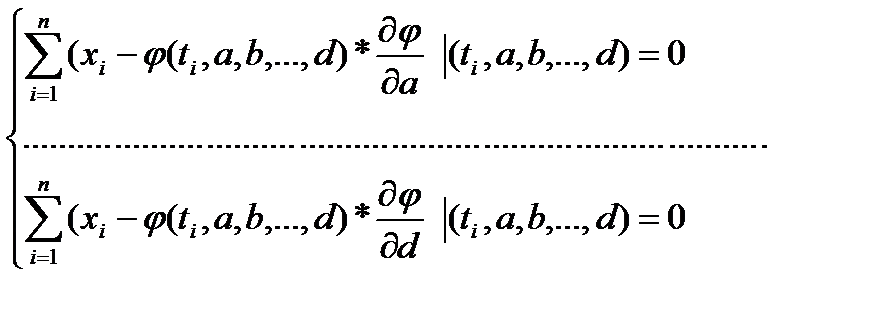(1)

Решая систему (1) находим a, b, …, d при которых минимум достигается.

Пусть функция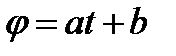

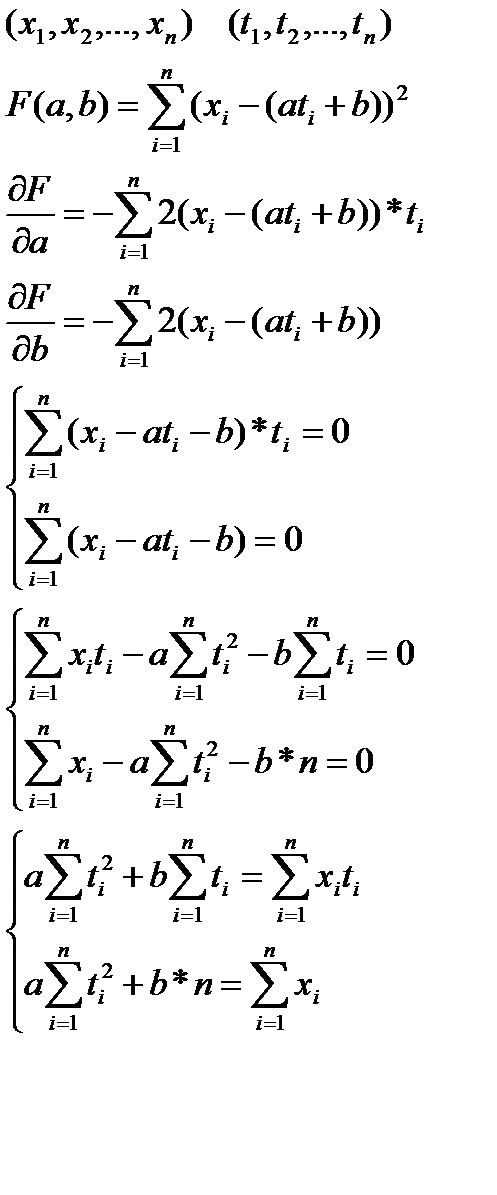
Тема: «Метод наибольшего правдоподобия»

При решении различных технических задач очень важно знать каким законам распределения подчиняются параметры, характеризующие изучаемый объект.

Закон распределения позволяет дать характеристику изучаемым объектам. Однако, знание общего вида закона распределения не дает возможности получать характеристики конкретного объекта, поскольку в законах распределения, как правило, присутствуют параметры, значение которых приходится определять по результатам эксперимента или наблюдений за объектом в течение некоторого промежутка времени.

Для рассмотрения метода наибольшего правдоподобия рассмотрим два случая:

1. случайная величина 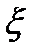является дискретной, ряд распределения которой имеет вид:

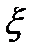	x1	x2	x3	…
p	p1( 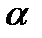)	p2( 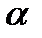)	p3( )	…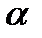

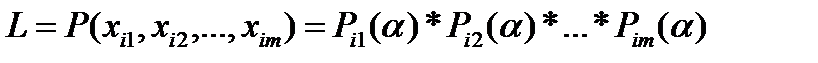
L – функция наибольшего правдоподобия

Принцип наибольшего правдоподобия состоит в том, что если событие произошло, то вероятность этого события является наибольшей, т.е. 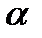предлагается выбирать таким образом, чтобы правая часть последнего равенства была наибольшей.

2. случайная величина 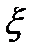задана своей плотностью вероятности 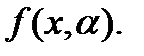Отметим, что параметр 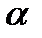может быть некоторым вектором (в первом случае тоже). В этом случае функция наибольшего правдоподобия пишется:

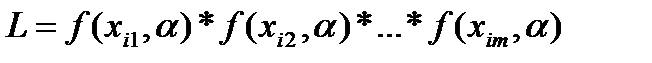
В этом случае считают, что 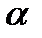нужно выбирать таким образом, чтобы функция правдоподобия принимала наибольшее значение.

Примеры.

Найти методом наибольшего правдоподобия по выборке 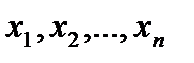точечную оценку неизвестного параметра 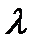распределения Пуассона:

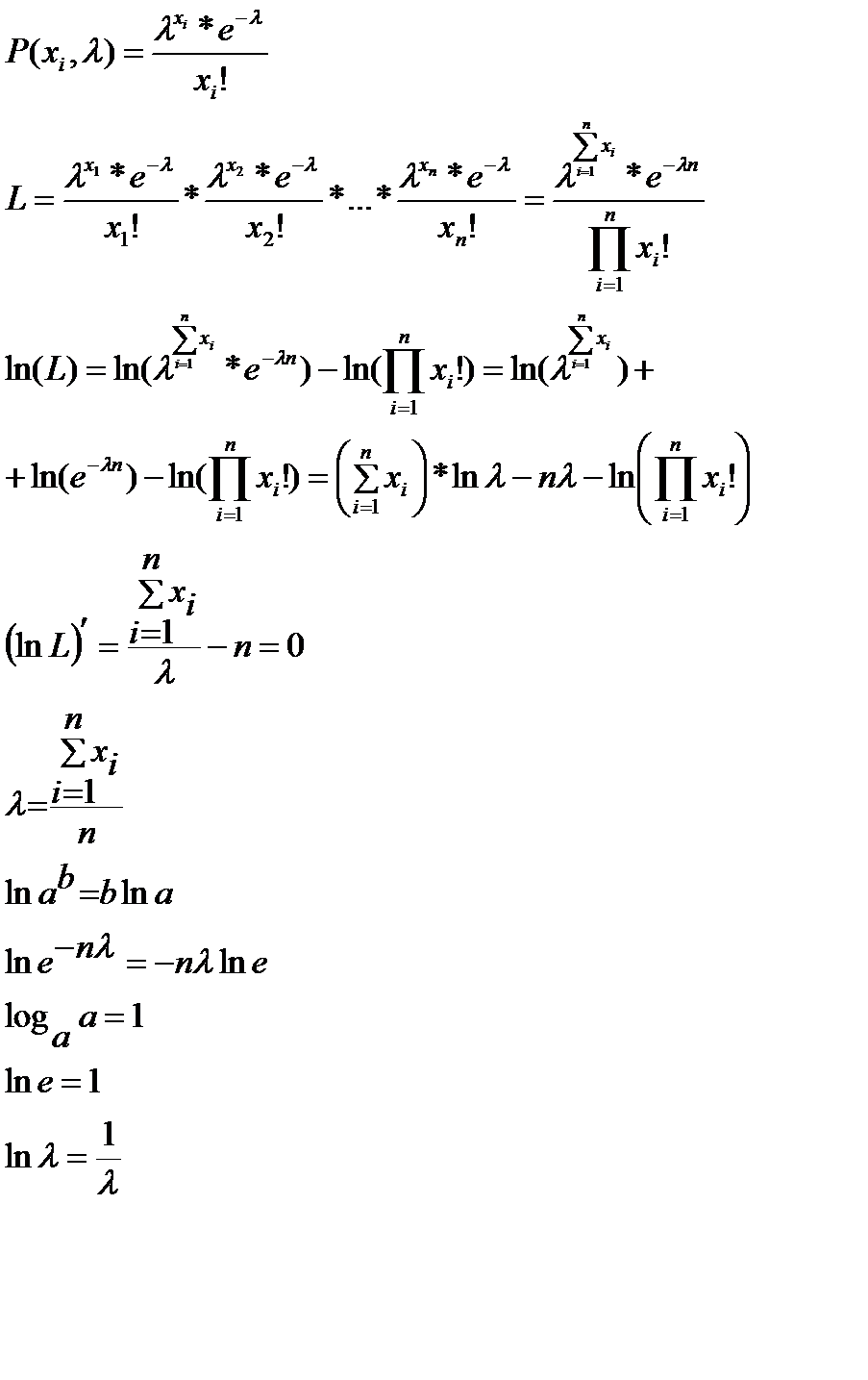
Найти методом наибольшего правдоподобия по выборке 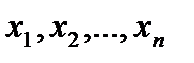точечную оценку неизвестного параметра 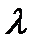показательного распределения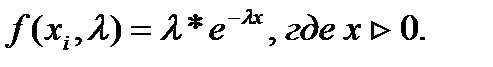

Найти методом наибольшего правдоподобия по выборке 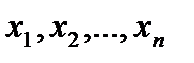точечную оценку неизвестного параметра 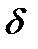распределения Реллея, плотность распределения которого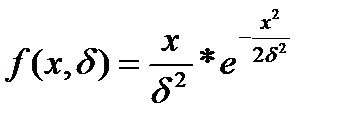

Тема: «Метод наименьших квадратов»

Предположим, что проводятся измерения через равные промежутки 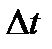некоторой функции x = x(t) - неизвестная функция. В результате измерений получают некоторый набор значений:

t	t1	t2	…	tn
x(t)	x1	x2	…	xn

Перед нами стоит задача выбрать аппроксимирующую функцию из некоторого класса функций 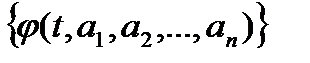такую, что сумма 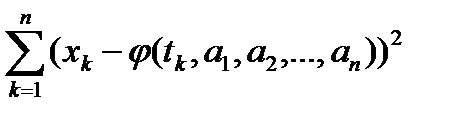будет минимальной, при этом подбираются неизвестные параметры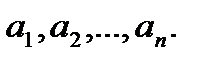

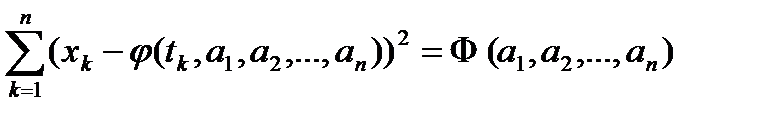
Необходимо найти минимум функции Ф.

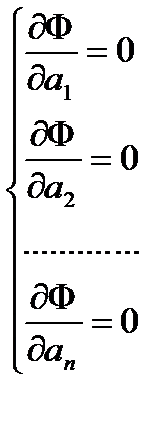
Решая систему нормальных уравнений, находим значения параметров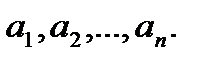

Пример.

Напишем систему нормальных уравнений для случая, когда в качестве класса функции выбирается система уравнений 1-ой степени.