Тема: «Понятие модели и моделирования. Математическое моделирование»
Тема: «Понятие модели и моделирования. Математическое моделирование»
Модель в широком смысле - это любой образ, аналог мысленный или реальный, изображение, описание, схема, чертеж, карта и т.п. какого-либо объекта, процесса или явления, используемый в качестве его заменителя или представителя. Сам объект, процесс или явление называется оригиналом данной модели.
Моделирование - это исследование какого-либо объекта или системы объектов путем построения и изучения их моделей. Это использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов.
На идее моделирования базируется практически любой метод научного исследования, при этом, в теоретических методах используются различного рода знаковые, абстрактные модели, в экспериментальных - предметные модели.
При исследовании сложное реальное явление заменяется некоторой упрощенной копией или схемой. Иногда построенная схема отражает какие-то существенные черты, позволяет разобраться в механизме явления, дает возможность предсказать его изменение. Одному и тому же явлению могут соответствовать разные модели.
Задача исследователя - предсказывать характер явления и ход процесса.
Из всей совокупности моделей мы выделим, и будем изучать как наиболее распространенные математические модели.
Существуют различные определения математических моделей.
1. Математическая модель — это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная цель моделирования — исследовать эти объекты и предсказать результаты будущих наблюдений.
2. Математической моделью называется некий математический объект, поставленный в соответствие реальному объекту и описывающий этот объект с требуемой точностью.
Математические модели могут быть детерменированными и стохастическими.
Стохастические модели – это модели использующие случайные величины, вероятностные методы и законы, а детерменированные модели - это модели, в которых отсутствует элемент случайности, в которых установлено взаимно-однозначное соответствие между переменными, описывающими объект или явления, и их изменения регламентируются строгими законами природы (физики, химии, биологии и т. д.), исключающими случайность.
По характеру режимов модели бывают статистическими и динамическими.
Статическая модель включает описание связей между основными переменными моделируемого объекта в установившемся режиме без учета изменения параметров, характеризующих объект.
В динамической модели описываются связи между основными переменными моделируемого объекта, при переходе от одного режима к другому, в процессе изменения каких-либо параметров (в частном случае, времени).
Модели бывают дискретными и непрерывными, а также смешанного типа.
В непрерывных переменные принимают значения из некоторого промежутка, в дискретных переменные принимают отдельные изолированные значения.
Математические модели, используемые в экономике, можно подразделять на макро- и микроэкономические.
Макроэкономические модели описывают экономику как единое целое, связывая между собой укрупненные материальные и финансовые показатели: валовый национальный продукт (ВНП), потребление, инвестиции, занятость, процентную ставку, количество денег и другие.
Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих экономики, либо поведение отдельной такой составляющей.
Пример.
Найти собственные числа (действительные) и соответствующие им собственные векторы матрицы.
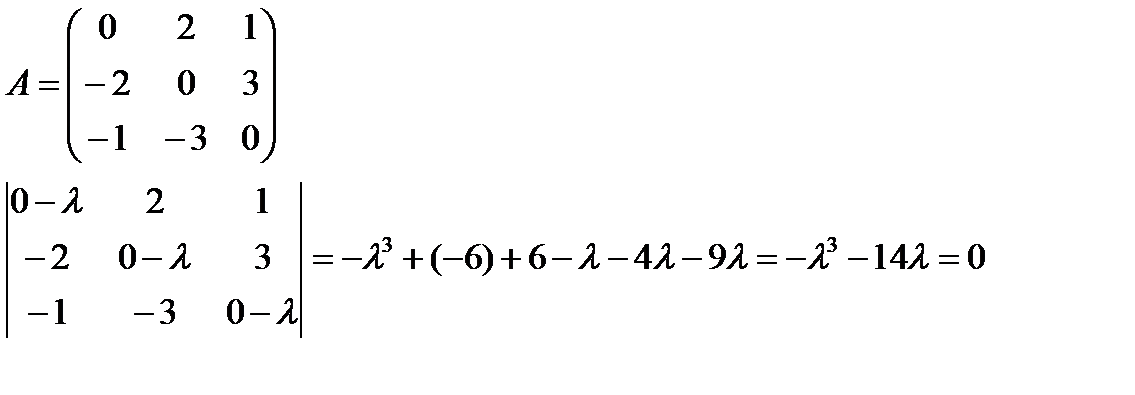
Пример.
Задана матрица парных сравнений 3 альтернатив. Проверить согласованность этой матрицы, провести ранжирование этих альтернатив методом парных сравнений (методом Саатти).
 |
 |
 |
 |
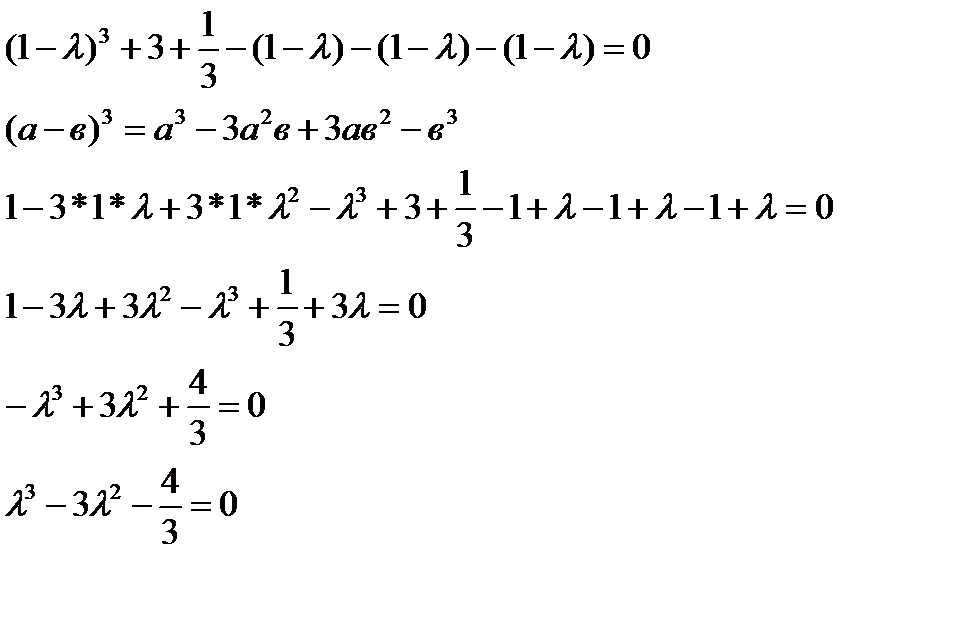
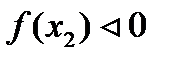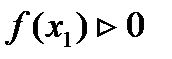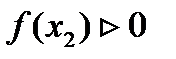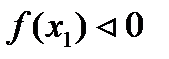| 3,136 |
| 3,1 |
| 3,15 |
| + |
| - |
| 2,8 |
| 3,2 |
| + |
| + |
| + |
| - |
| 3,1 |
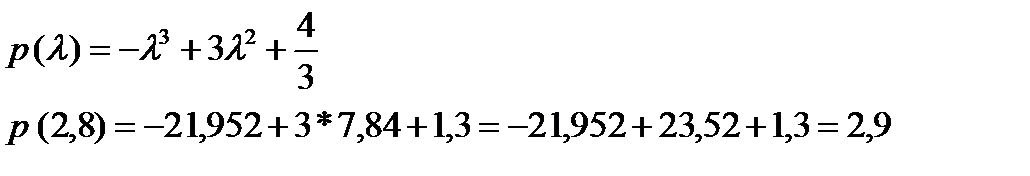
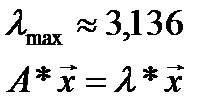
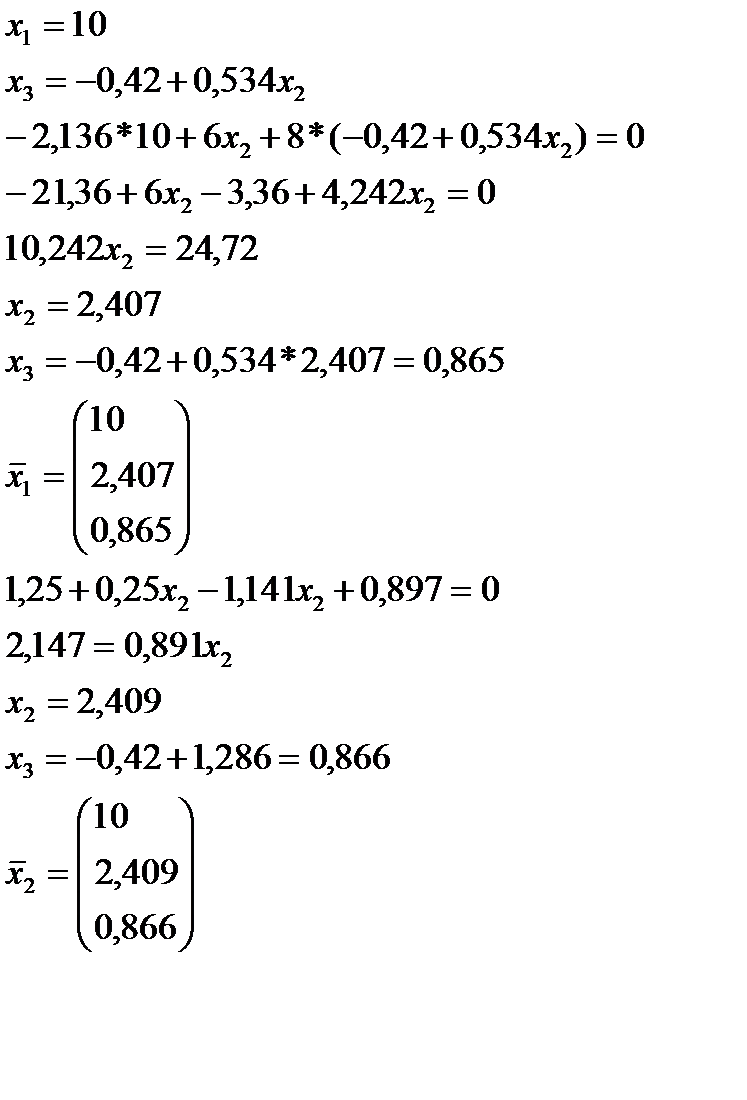
Индекс согласованности:
IC =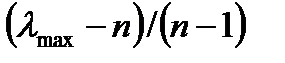 
= (3,136-3) / (3-1) = 0,068
Оценка согласованности:
ОС = 0,068 / 0,58 = 0,117
Пример.
Матрица парных сравнений:
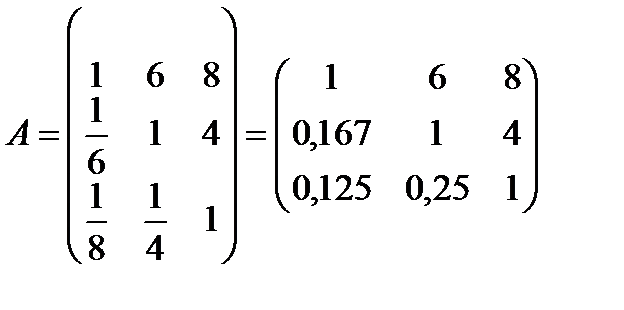
Суммы элементов столбцов:
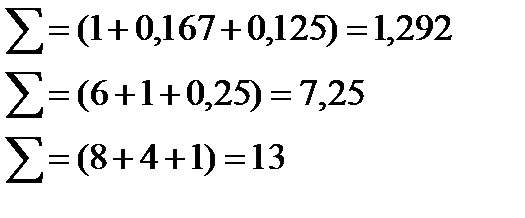
Матрица с нормированными столбцами:
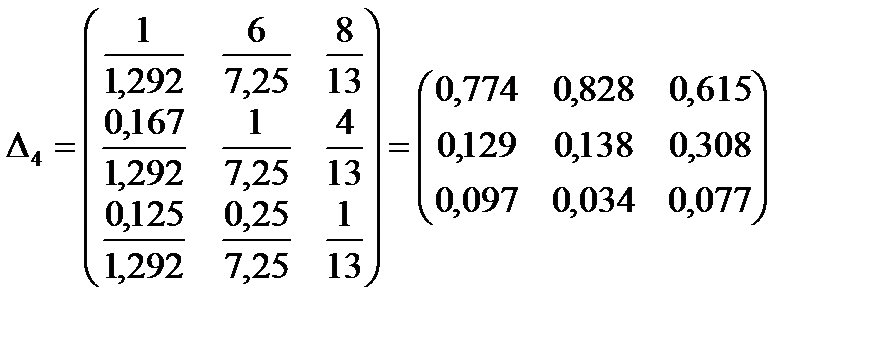
Матрица средних значений (по строкам):
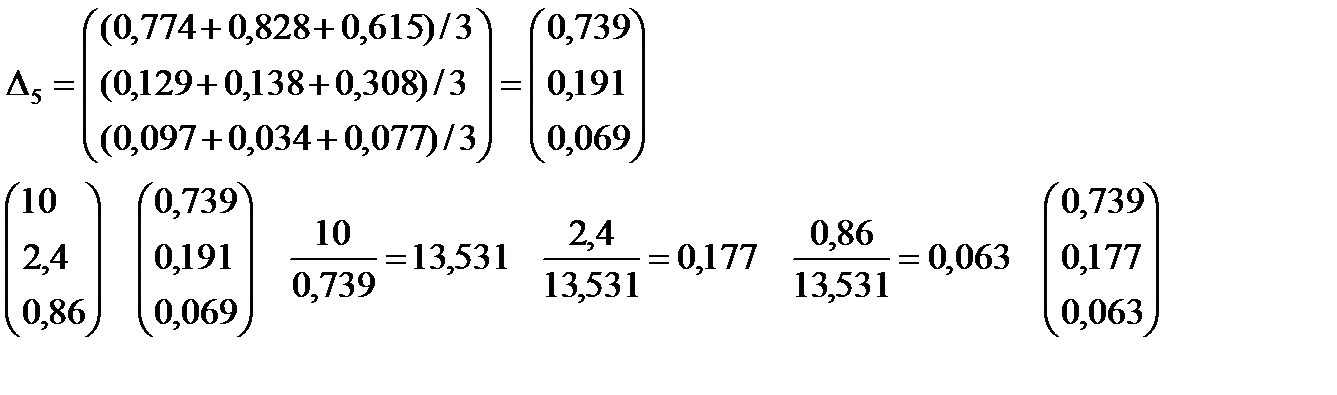
Примеры.
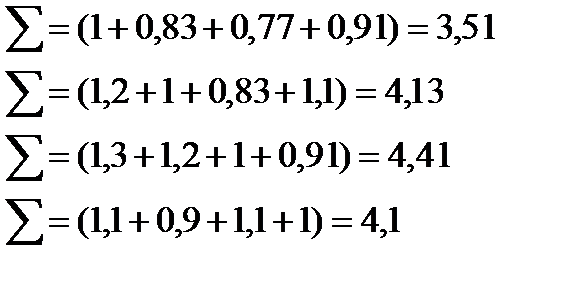
Тема: «Математическое моделирование поддержки принятия решений на основе использования теории нечетких множеств».
Пример.
Работник за m месяцев получал зарплату:
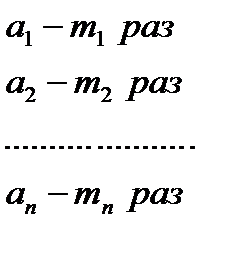
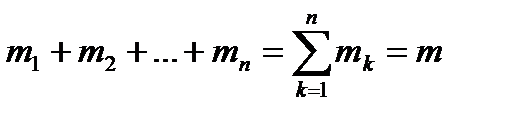- количество месяцев
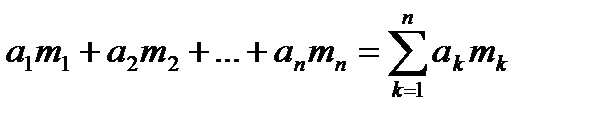- полученный заработок за m месяцев
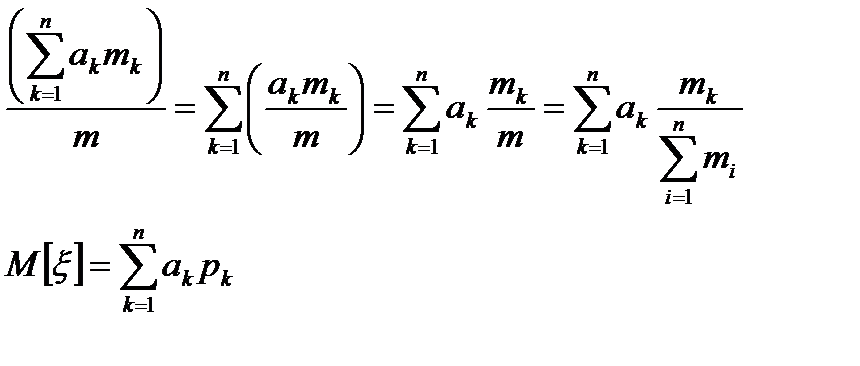
где M - математическое ожидание;
pk - вероятность получить зарплату ak.
Пример.
| № | Модель | Цена | Двухсимкартный | Дисплей | Процессор | ОЗУ | Емкость аккумулятора | Вес |
| Samsung Galaxy SM-J 120F | -8990 | + | 4,5 | -131 | ||||
| Samsung Galaxy SM-J 320F | -11290 | + | 1,5 | -138 | ||||
| Samsung Galaxy SM-J 105F | -5490 | + | 0,768 | -123 | ||||
| Samsung A3 SM-A300F | -14990 | + | 4,5 | -110 | ||||
| Максимальное значение | -14990 | + | 1,5 | -138 |
Критерий двухсимкартный можно опустить, так как у всех моделей смартфонов он присутствует.
Построим матрицу соответствия альтернатив критериям, для этого каждый элемент делим на максимальное значение по столбцам и проранжируем по степени важности каждый критерий в баллах от 1 до 10.
| № | Цена (y1) | Дисплей (y2) | Процессор (y3) | ОЗУ (y4) | Емкость аккумулятора (y5) | Вес (y6) |
| -0,6 | 0,9 | 0,87 | 0,67 | 0,79 | -0,95 | |
| -0,75 | -1 | |||||
| -5490 | 0,8 | 0,8 | 0,5 | 0,58 | -0,89 | |
| -0,37 | 0,9 | 0,8 | 0,67 | 0,73 | -0,8 | |
| Баллы |
Находим вес каждого критерия по нечеткому множеству В:
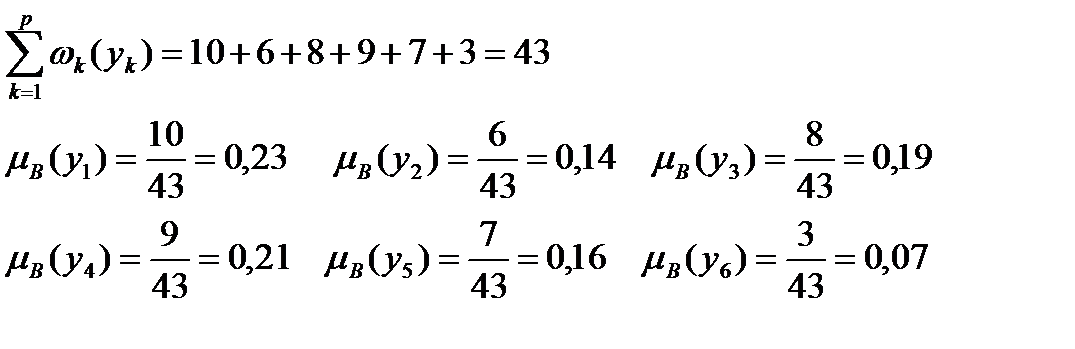
Находим функции принадлежности:
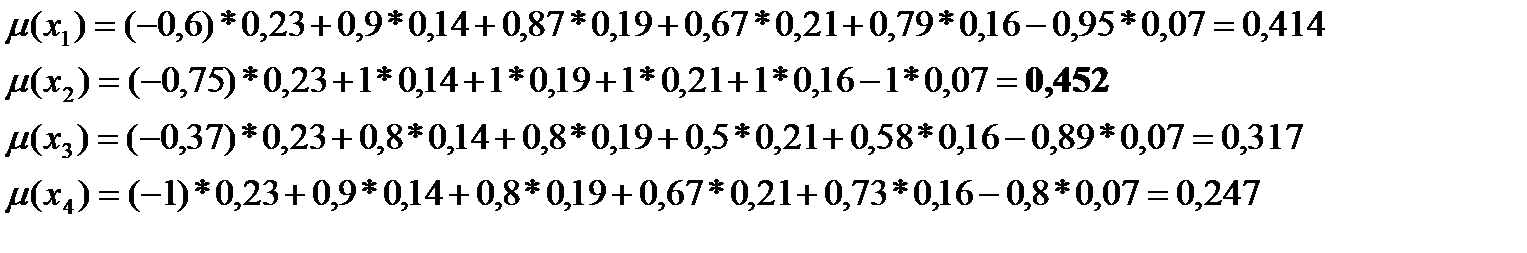
Примеры.
Найти методом наибольшего правдоподобия по выборке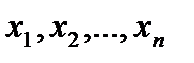 
точечную оценку неизвестного параметра 
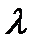распределения Пуассона:
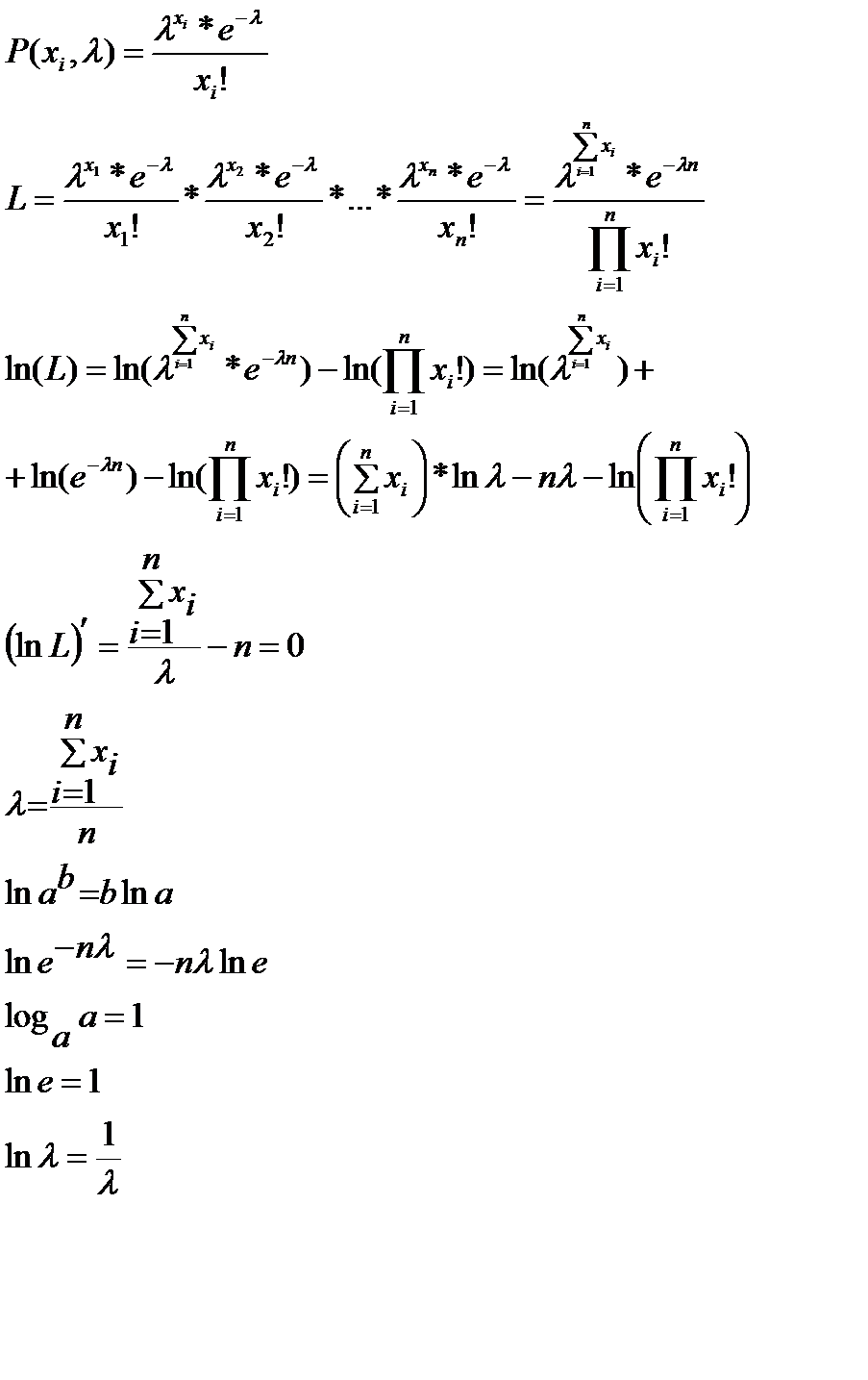
Найти методом наибольшего правдоподобия по выборке 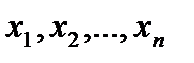точечную оценку неизвестного параметра 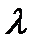показательного распределения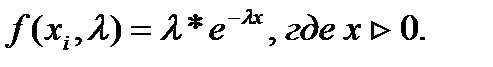 
Найти методом наибольшего правдоподобия по выборке 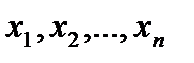точечную оценку неизвестного параметра 
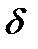распределения Реллея, плотность распределения которого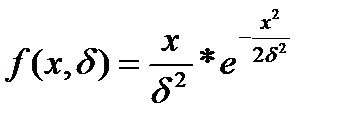 
Пример.
Напишем систему нормальных уравнений для случая, когда в качестве класса функции выбирается система уравнений 1-ой степени.
Тема: «Понятие модели и моделирования. Математическое моделирование»
Модель в широком смысле - это любой образ, аналог мысленный или реальный, изображение, описание, схема, чертеж, карта и т.п. какого-либо объекта, процесса или явления, используемый в качестве его заменителя или представителя. Сам объект, процесс или явление называется оригиналом данной модели.
Моделирование - это исследование какого-либо объекта или системы объектов путем построения и изучения их моделей. Это использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов.
На идее моделирования базируется практически любой метод научного исследования, при этом, в теоретических методах используются различного рода знаковые, абстрактные модели, в экспериментальных - предметные модели.
При исследовании сложное реальное явление заменяется некоторой упрощенной копией или схемой. Иногда построенная схема отражает какие-то существенные черты, позволяет разобраться в механизме явления, дает возможность предсказать его изменение. Одному и тому же явлению могут соответствовать разные модели.
Задача исследователя - предсказывать характер явления и ход процесса.
Из всей совокупности моделей мы выделим, и будем изучать как наиболее распространенные математические модели.
Существуют различные определения математических моделей.
1. Математическая модель — это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная цель моделирования — исследовать эти объекты и предсказать результаты будущих наблюдений.
2. Математической моделью называется некий математический объект, поставленный в соответствие реальному объекту и описывающий этот объект с требуемой точностью.
Математические модели могут быть детерменированными и стохастическими.
Стохастические модели – это модели использующие случайные величины, вероятностные методы и законы, а детерменированные модели - это модели, в которых отсутствует элемент случайности, в которых установлено взаимно-однозначное соответствие между переменными, описывающими объект или явления, и их изменения регламентируются строгими законами природы (физики, химии, биологии и т. д.), исключающими случайность.
По характеру режимов модели бывают статистическими и динамическими.
Статическая модель включает описание связей между основными переменными моделируемого объекта в установившемся режиме без учета изменения параметров, характеризующих объект.
В динамической модели описываются связи между основными переменными моделируемого объекта, при переходе от одного режима к другому, в процессе изменения каких-либо параметров (в частном случае, времени).
Модели бывают дискретными и непрерывными, а также смешанного типа.
В непрерывных переменные принимают значения из некоторого промежутка, в дискретных переменные принимают отдельные изолированные значения.
Математические модели, используемые в экономике, можно подразделять на макро- и микроэкономические.
Макроэкономические модели описывают экономику как единое целое, связывая между собой укрупненные материальные и финансовые показатели: валовый национальный продукт (ВНП), потребление, инвестиции, занятость, процентную ставку, количество денег и другие.
Микроэкономические модели описывают взаимодействие структурных и функциональных составляющих экономики, либо поведение отдельной такой составляющей.