Дайте определение случайной величины и раскройте ее классификацию.

Дайте определение случайной величины и раскройте ее классификацию.

Случайная величина — это переменная, значения которой представляют собой исходы какого-нибудь случайного феномена или эксперимента. Простыми словами: это численное выражение результата случайного события. Случайная величина является одним из основных понятий теории вероятностей.^[1]

Для обозначения случайной величины в математике принято использовать заглавный вариант буквы "икс" {\displaystyle X}. Если определять случайную величину более строго, то она уже не переменная {\displaystyle X}, а функция {\displaystyle y=X(\omega )} , значения {\displaystyle y} которой численно выражают исходы {\displaystyle \omega } случайного феномена. Одним из требований к данной функции будет её измеримость, что служит для отсеивания патологических случаев, когда значения данной функции {\displaystyle X(\omega )} бесконечно чувствительны к малейшим изменениям в исходах случайного феномена, эксперимента.

Важно понимать, что, как функция, случайная величина {\displaystyle X(\omega )} не возвращает вероятностью наступления события {\displaystyle \omega }, а возвращает численное выражение исхода {\displaystyle \omega }. Пусть, например, экспериментатор тянет наугад одну из карт в колоде игральных карт. Тогда {\displaystyle \omega } будет представлять одну из вытянутых карт; понятно что здесь {\displaystyle \omega } не число, а карта - физический объект, название которого обозначается через символ {\displaystyle \omega }. Тогда функция {\displaystyle X(\omega )}, принимая в качестве аргумента "название" объекта, вернёт уже число с которым мы будем в дальнейшем ассоциировать карту {\displaystyle \omega }. Пусть в нашем случае экспериментатор вытянул Короля Крести, т.е. {\displaystyle \omega =K_{\clubsuit }} , тогда после подставления этого исхода в функцию {\displaystyle X(K_{\clubsuit })}, мы получим уже число, например, 13. Это число не является вероятностью вытягивания короля из колоды или любой другой карты. Это число является результатом перевода объекта из физического мира в объект математического мира, ведь с числом 13 уже можно проводить математические операции, в то время как с объектом {\displaystyle K_{\clubsuit }} эти операции проводить было нельзя.

Примером объектов, для представления состояния которых требуется применение случайных величин являются микроскопические объекты, описываемые квантовой механикой. Случайными величинами описываются события передачи наследственных признаков от родительских организмов к их потомкам (см. Законы Менделя). К случайным относятся события радиоактивного распада ядер атомов.

Классификация

Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения. Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные (смешанные).

На схеме испытаний может быть определена как отдельная случайная величина (одномерная/скалярная), так и целая система одномерных взаимосвязанных случайных величин (многомерная/векторная).

· Пример смешанной случайной величины — время ожидания при переходе через автомобильную дорогу в городе на нерегулируемом перекрёстке.

· В бесконечных схемах (дискретных или непрерывных) уже изначально элементарные исходы удобно описывать количественно. Например, номера градаций типов несчастных случаев при анализе ДТП; время безотказной работы прибора при контроле качества и т. п.

· Числовые значения, описывающие результаты опытов, могут характеризовать не обязательно отдельные элементарные исходы в схеме испытаний, но и соответствовать каким-то более сложным событиям.

С одной стороны, с одной схемой испытаний и с отдельными событиями в ней одновременно может быть связано сразу несколько числовых величин, которые требуется анализировать совместно.

· Например, координаты (абсцисса, ордината) какого-то разрыва снаряда при стрельбе по наземной цели; метрические размеры (длина, ширина и т. д.) детали при контроле качества; результаты медобследования (температура, давление, пульс и пр.) при диагностике больного; данные переписи населения (по возрасту, полу, достатку и пр.).

Поскольку значения числовых характеристик схем испытания соответствуют в схеме некоторым случайным событиям (с их определёнными вероятностями), то и сами эти значения являются случайными (с теми же вероятностями). Поэтому такие числовые характеристики и принято называть случайными величинами. При этом расклад вероятностей по значениям случайной величины называется законом распределения случайной величины.

Определение

Функция распределения случайной величины 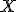- это числовая функция, которая имеет вид:

, .

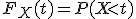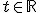Обозначение 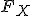используется для того, чтобы подчеркнуть, о какой случайной величине идет речь; если это ясно из контекста, то часто индекс опускают и обозначают функцию распределения просто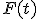

Свойства

Функция распределения 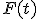определена на всей числовой оси и обладает следующими свойствами, вытекающими из свойств вероятностной меры:

1.

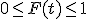
2. , .

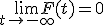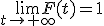3. Функция распределения является неубывающей: если 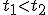, то

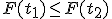
4. Функция распределения непрерывна слева: 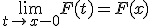для любого .

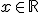Примечание. Последнее свойство обозначает, какие значения принимает функция распределения в точках разрыва. Иногда определение функции распределения формулируют с использованием нестрогого неравенства: 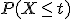. В этом случае непрерывность слева заменяется на непрерывность справа: 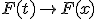при 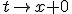. Никакие содержательные свойства функции распределения при этом не меняются, поэтому данный вопрос является лишь терминологическим.

Свойства 1-4 являются характеристическими, т.е. любая функция 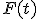, удовлетворяющая этим свойствам, является функцией распределения некоторой случайной величины.

Функция распределения задает распределение вероятностей случайной величины однозначно. Фактически, она является универсальным и наиболее наглядным способом описания этого распределения.

Чем сильнее функция распределения растет на заданном интервале числовой оси, тем выше вероятность попадания случайной величины в этот интервал. Если вероятность попадания в интервал равна нулю, то функция распределения на нем постоянна.

В частности, вероятность того, что случайная величина 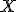примет заданное значение 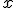, равна скачку функции распределения в данной точке:

.

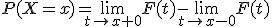Если функция распределения непрерывна в точке 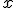, то вероятность принять данное значение для случайной величины равна нулю. В частности, если функция распределения непрерывна на всей числовой оси (при этом и соответствующее распределение называется непрерывным), то вероятность принять любое заданное значение равна нулю.

Из определения функции распределения вытекает, что вероятность попадания случайной величины в интервал, замкнутый слева и открытый справа, равна:

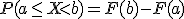
С помощью данной формулы и указанного выше способа нахождения вероятности попадания в любую заданную точку, легко определяются вероятности попадания случайной величины в интервалы других типов: 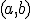, 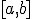и 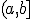. Далее, по теореме о продолжении меры, можно однозначно продолжить меру на все борелевские множества числовой прямой 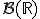. Для того, чтобы применить эту теорему, требуется показать, что таким образом определенная на интервалах мера является на них сигма-аддитивной; при доказательстве этого в точности используются свойства 1-4 (в частности, свойство непрерывности слева 4, поэтому отбросить его нельзя).

QED

Для доказательства остальных свойств нам понадобится свойство непрерывности вероятностной меры.

Доказательство свойства (F2). Заметим сначала, что существование пределов в свойствах (F2), (F3) вытекает из монотонности и ограниченности функции 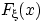. Остается лишь доказать равенства

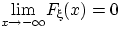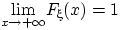, и .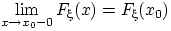

Для этого в каждом случае достаточно найти предел по какой-нибудь подпоследовательности 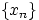, так как существование предела влечёт совпадение всех частичных пределов.

Докажем, что 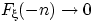при 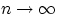. Рассмотрим вложенную убывающую последовательность событий :

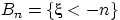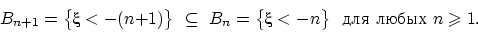
Пересечение 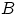всех этих событий состоит из тех и только тех 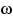, для которых 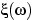меньше любого вещественного числа. Но для любого элементарного исхода 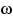значение 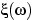вещественно, и не может быть меньше всех вещественных чисел. Иначе говоря, пересечение событий 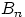не содержит элементарных исходов, т.е. 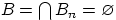. По свойству непрерывности меры, 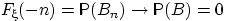при .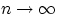

Точно так же докажем остальные свойства.

Покажем, что 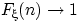при 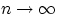, т.е. 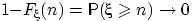. Обозначим через 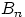событие 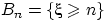. События 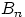вложены:

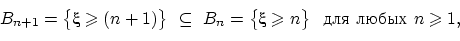
а пересечение 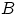этих событий снова пусто — оно означает, что 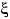больше любого вещественного числа. По свойству непрерывности меры, 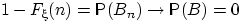при .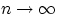

Доказательство свойства (F3). Достаточно доказать, что 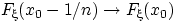при 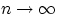. Иначе говоря, доказать сходимость к нулю следующей разности:

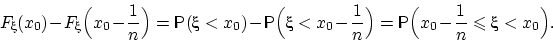
Следующая теорема говорит о том, что три доказанных свойства полностью описывают класс функций распределения. То, что любая функция распределения ими обладает, мы с вами доказали, а теорема утверждает, что любая функция с такими свойствами есть функция распределения.

Теорема 21.Если функция 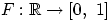удовлетворяет свойствам (F1)—(F3), то 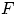есть функция распределения некоторой случайной величины 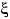, т.е. найдётся вероятностное пространство 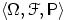и случайная величина 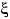на нём такая, что .

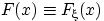Эту теорему мы доказывать не станем. Хотя её можно попробовать доказать конструктивно — предъявив то вероятностное пространство (проще всего отрезок 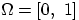с 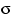-алгеброй борелевских множеств и мерой Лебега) и ту случайную величину, о существовании которых идёт речь.

(F4)

В любой точке 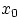разниц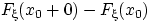а равна :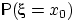

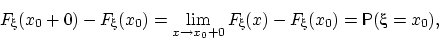
или, иначе говоря, .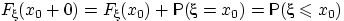

Замечание 13.Очень часто функцией распределения называют 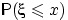. Эта функция отличается от определённой выше лишь тем, что она непрерывна справа, а не слева. Соответственно, вероятность 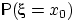для неё равна величине скачка слева, а не справа.

(F5)

Для любой случайной величины 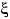имеет место равенство:

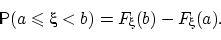(13)

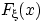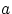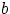Если же функция распределения непрерывна в точках и , то

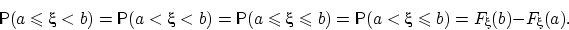
Доказательство.Докажем только равенство (13). Все остальные равенства следуют из него и свойства (F4).

Заметим, что 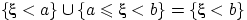, и первые два события несовместны. Поэтому 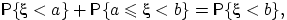или 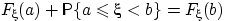, что и требовалось доказать.

QED

Необходимость выборки

· Объект исследования очень обширный. Например, потребители продукции глобальной компании – огромное количество территориально разбросанных рынков.

· Существует необходимость в сборе первичной информации.

Объём выборки

Объём выборки — число случаев, включённых в выборочную совокупность. Из статистических соображений рекомендуется, чтобы число случаев составляло не менее 30 – 35.

Репрезентативность

Выборка может рассматриваться в качестве репрезентативной или нерепрезентативной.

Метод

Объём данных (измеренные значения, данные обследования) является первым оригинальным неупорядоченным списком. Во-первых, его необходимо отсортировать. От первоначального списка, в этом случае, может возникнуть небольшое отклонение квантилей (статистический разброс), вероятного отклонения и стандартного отклонения (эмпирическое правило: стандартное отклонение = расстояние / 6).

Затем мы приписываем каждой величине значение и суммируем их. Как правило мы получаем абсолютную частоту. Опираясь на данные абсолютной частоты вычисляем общее количество значений выборки и вычисляем относительные частоты. Теперь у нас есть упорядоченное множество пар значений (характерные значения и связанных с ними относительные частоты), так называемый рейтинг.

Добавим относительные частоты, начиная с наименьшего значения признака и назначим каждой функции значение суммы (в том числе его собственного вклада), так чтобы получилось распределение. Это указывает для каждого значения признака, насколько велика его доля, меньших или равных соответствующего характеристического значения. Процент начинается с 0 и приближается к 1 или 100 процентам. Графически это изображается слабой монотонно возрастающей кривой, имеющей удлиненную S-образную форму. Существуют многочисленные попытки воспроизведения результатов распределения функциональными уравнениями. Распределение суммы, в зависимости от значений признаков самый простой тип представления распределения частот.

По правилам также необходимо произвести классификацию характерных значений. Эта процедура делит диапазон значений, возникающих, например, в 10 или 20 одинаковой ширины классов (редких значений по краям (см. «выбросы») иногда группирующихся вместе в большими классами). Затем определяется плотность функции, производной функции распределения в соответствии с характеристикой значения в случае непрерывного распределения. Кроме того, частоту можно определить не только путём подсчета, но также, например, путём взвешивания. Тогда мы получим распределение массы вместо ряда распределения. В принципе, можно воспользоваться любой аддитивной величиной для измерения частоты. Если случайная выборка сильно отличается от нормального распределения (кривой нормального распределения), то данные могут быть смещены с помощью выбора эффектов или тенденций. Различные статистические тесты предлагают вывод или дисперсионный анализ. Если размер выборки находится в суперпозиции нескольких подмножеств (возрастное распределение, профессий, групп), то распределение частот вместо максимальных также может быть двух-или многомерным.

Пример 1. Бригада из 6 рабочих получает в месяц 3 3,2 3,3 3,5 3,8 3,1 тыс.руб.

Найти среднюю заработную плату
Решение: (3 + 3,2 + 3,3 +3,5 + 3,8 + 3,1) / 6 = 3,32 тыс. руб.

Пример 2. Найти среднюю заработную плату рабочих цеха за месяц

Заработная плата одного рабочего тыс.руб; X	Число рабочих F
3,2
3,3
3,4
4,0
Итого:

Средняя заработная плата может быть получена путем деления общей суммы заработной платы на общее число рабочих:

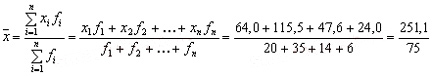
Ответ: 3,35 тыс.руб.

Геометрическая простая

Для расчетов средней геометрической простой используется формула:

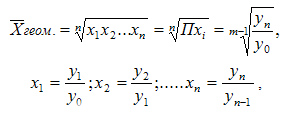
где:

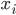§ — цепной коэффициент роста

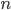§ — число этих коэффициентов роста

§ П — знак произведения

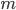§ — количество уровней ряда

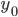§ — значение начального уровня ряда

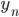§ — значение конечного уровня ряда

Геометрическая взвешенная

Для определения средней геометрической взвешенной применяется формула:

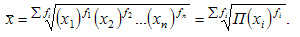
Средняя гармоническая — используется в тех случаях когда известны индивидуальные значения признака 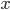и произведение 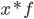, а частоты 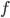неизвестны.

В примере ниже 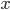— урожайность известна, 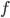— площадь неизвестна (хотя её можно вычислить делением валового сбора зерновых на урожайность), 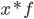— валовый сбор зерна известен.

Среднегармоническую величину можно определить по следующей формуле:

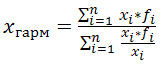
Формула средней гармонической:

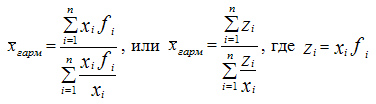
Пример. Вычислить среднюю урожайность по трем фермерским хозяйствам

Фермерское хозяйство	Урожайность ц/га (х)	Валовый сбор зерновых Ц (z = x*f)
	18,2
	20,4
	23,5
Итого

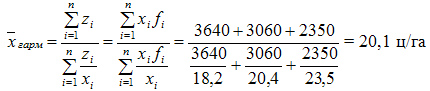
Ответ: 20,1 ц/га

Гармоническая простая

В тех случаях, когда произведение 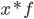одинаково или равно 1 (z = 1) для расчета применяют среднюю гармоническую простую, вычисляемую по формуле:

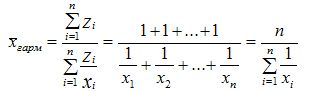
Средняя гармоническая простая — показатель, обратный средней арифметической простой, исчисляемый из обратных значений признака.

Средняя квадратическая

Средние диаметры колес, труб, средние стороны квадратов определяются при помощи средней квадратической.

Среднеквадратические величины используются для расчета некоторых показателей, например коэффициент вариации, характеризующего ритмичность выпуска продукции. Здесь определяют среднеквадратическое отклонение от планового выпуска продукции за определенный период по следующей формуле:

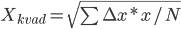
Эти величины точно характеризуют изменение экономических показателей по сравнению с их базисной величиной, взятое в его усредненной величине.

Квадратическая простая

Средняя квадратическая простая вычисляется по формуле:

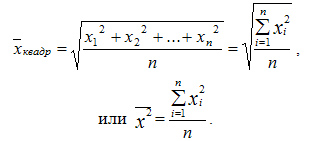
Квадратическая взвешенная

Средняя квадратическая взвешенная равна:

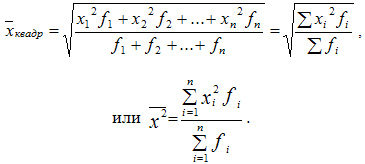
Дайте определение ряда мажорантности.

Если каждый член положительного ряда не больше, чем имеющий тот же номер член другого ряда, то второй ряд называется мажорантным по отношению к первому.

Иначе говоря, ряд

b₁ + b₂ + b₃ + ...

является мажорантным по отношению к ряду

a₁ + a₂ + a₃ + ...,

если при всех n будет

a_n ≤ b_n.

Легко понять, что частичная сумма данного ряда не больше, чем (имеющая тот же номер) частичная сумма ряда мажорантного. Значит, если ограничены сверху частичные суммы мажорантного ряда, то это и подавно так для исходного ряда. Отсюда вытекает

Теорема 2. Если для положительного ряда существует сходящийся мажорантный ряд, то и сам этот ряд сходится. Если же данный ряд расходится, то расходится и всякий мажорантный для него ряд.

Рассмотрим, например, ряд

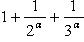
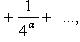(27)

предполагая α < 1. Ясно, что этот ряд - мажорантный по отношению к гармоническому ряду, и потому ряд (27) расходится.

Исследование сходимости какого-либо ряда при помощи теоремы 2 наталкивается на необходимость нахождения другого ряда, поведение которого в отношении его сходимости нам известно и с которым мы хотим сравнить наш исходный ряд. Нахождение такого "ряда сравнения" в значительной степени зависит от проницательности исследователя, и в этом существенный недостаток признака сравнения. Существуют признаки сходимости, носящие гораздо более алгорифмический характер. Остановимся только на одном из таких признаков - на признаке Даламбера.

Лемма 1. Если строго положительный ряд

a₁ + a₂ + a₃ + ... (28)

таков, что при всех n оказывается

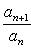
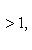
то этот ряд расходится.

В самом деле, здесь a_n+1 > a_n, т. е. общий член ряда возрастает с увеличением своего номера и не может стремиться к нулю. Иначе говоря, не выполнено необходимое условие сходимости ряда.

Дайте определение случайной величины и раскройте ее классификацию.

Случайная величина — это переменная, значения которой представляют собой исходы какого-нибудь случайного феномена или эксперимента. Простыми словами: это численное выражение результата случайного события. Случайная величина является одним из основных понятий теории вероятностей.^[1]

Для обозначения случайной величины в математике принято использовать заглавный вариант буквы "икс" {\displaystyle X}. Если определять случайную величину более строго, то она уже не переменная {\displaystyle X}, а функция {\displaystyle y=X(\omega )} , значения {\displaystyle y} которой численно выражают исходы {\displaystyle \omega } случайного феномена. Одним из требований к данной функции будет её измеримость, что служит для отсеивания патологических случаев, когда значения данной функции {\displaystyle X(\omega )} бесконечно чувствительны к малейшим изменениям в исходах случайного феномена, эксперимента.

Важно понимать, что, как функция, случайная величина {\displaystyle X(\omega )} не возвращает вероятностью наступления события {\displaystyle \omega }, а возвращает численное выражение исхода {\displaystyle \omega }. Пусть, например, экспериментатор тянет наугад одну из карт в колоде игральных карт. Тогда {\displaystyle \omega } будет представлять одну из вытянутых карт; понятно что здесь {\displaystyle \omega } не число, а карта - физический объект, название которого обозначается через символ {\displaystyle \omega }. Тогда функция {\displaystyle X(\omega )}, принимая в качестве аргумента "название" объекта, вернёт уже число с которым мы будем в дальнейшем ассоциировать карту {\displaystyle \omega }. Пусть в нашем случае экспериментатор вытянул Короля Крести, т.е. {\displaystyle \omega =K_{\clubsuit }} , тогда после подставления этого исхода в функцию {\displaystyle X(K_{\clubsuit })}, мы получим уже число, например, 13. Это число не является вероятностью вытягивания короля из колоды или любой другой карты. Это число является результатом перевода объекта из физического мира в объект математического мира, ведь с числом 13 уже можно проводить математические операции, в то время как с объектом {\displaystyle K_{\clubsuit }} эти операции проводить было нельзя.

Примером объектов, для представления состояния которых требуется применение случайных величин являются микроскопические объекты, описываемые квантовой механикой. Случайными величинами описываются события передачи наследственных признаков от родительских организмов к их потомкам (см. Законы Менделя). К случайным относятся события радиоактивного распада ядер атомов.

Классификация

Случайные величины могут принимать дискретные, непрерывные и дискретно-непрерывные значения. Соответственно случайные величины классифицируют на дискретные, непрерывные и дискретно-непрерывные (смешанные).

На схеме испытаний может быть определена как отдельная случайная величина (одномерная/скалярная), так и целая система одномерных взаимосвязанных случайных величин (многомерная/векторная).

· Пример смешанной случайной величины — время ожидания при переходе через автомобильную дорогу в городе на нерегулируемом перекрёстке.

· В бесконечных схемах (дискретных или непрерывных) уже изначально элементарные исходы удобно описывать количественно. Например, номера градаций типов несчастных случаев при анализе ДТП; время безотказной работы прибора при контроле качества и т. п.

· Числовые значения, описывающие результаты опытов, могут характеризовать не обязательно отдельные элементарные исходы в схеме испытаний, но и соответствовать каким-то более сложным событиям.

С одной стороны, с одной схемой испытаний и с отдельными событиями в ней одновременно может быть связано сразу несколько числовых величин, которые требуется анализировать совместно.

· Например, координаты (абсцисса, ордината) какого-то разрыва снаряда при стрельбе по наземной цели; метрические размеры (длина, ширина и т. д.) детали при контроле качества; результаты медобследования (температура, давление, пульс и пр.) при диагностике больного; данные переписи населения (по возрасту, полу, достатку и пр.).

Поскольку значения числовых характеристик схем испытания соответствуют в схеме некоторым случайным событиям (с их определёнными вероятностями), то и сами эти значения являются случайными (с теми же вероятностями). Поэтому такие числовые характеристики и принято называть случайными величинами. При этом расклад вероятностей по значениям случайной величины называется законом распределения случайной величины.