Марковская модель расчета Вероятности

Безопасного полета

Оценка БзП при воздействии на ЛА факторов, вероятность появления которых зависит от времени полета, может быть проведена на основе представления переходов системы от од­ного состояния к другому под воздействием опасных факторов моделью марковского процесса со счетным множеством состоя­ний и непрерывным временем. Факторы при этом могут быть как зависимые, так и независимые, однократно возникающие и мно­гократно повторяющиеся, с зависимыми и независимыми послед­ствиями, то есть такая модель позволяет получить оценку БзП с учетом воздействия на ЛА обширного класса опасных факто­ров. Допустим, что все возможные в полете особые ситуации, вызванные опасными факторами, образуют счетное множество 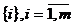. В зависимости от успешности действий экипажа по парированию последствий опасных факторов множеству 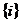бу­дут соответствовать два подмножества: 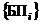– благополуч­ных исходов и 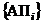– неблагополучных исходов полета.

Обозначим вероятности этих исходов соответственно 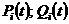. Так как события из множества 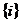для текущего момента времени полета являются несовместным, то на основании теоремы сложения вероятностей можно записать

,

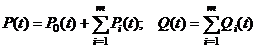где 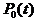– вероятность пребывания системы в нормальном состоянии.

Неизвестные вероятности 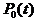, , 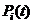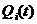вычисляются по модели марковского процесса смены состояний рас­сматриваемой системы.

Для обоснования возможности применения такой модели ис­пользуются следующие допущения:

1. События парирования или непарирования возникают однов­ременно с появлением опасных факторов, вызывающих особую си­туацию.

2. Последовательность возникновения особых ситуаций i-го типа является простейшим потоком с интенсивностью 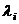. Соответствующие ему потоки благополучных и неблагополучных исходов в силу принятого допущения также являются простейши­ми. Их интенсивности соответственно равны , .

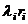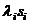3. Отказавшие в полете элементы не восстанавливаются, а ошибки операторов не повторяются.

Напомним, что в силу ранее принятого допущения (см. п. 1.4) ситуация в начале полета является нормальной, то есть опасные факторы отсутствуют. Для расчета вероятностей 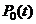, , 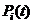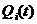марковский процесс со всеми выявленными и реально возможными в полете состояниями системы представляется наг­лядно в виде графа состояний (рис. 1.8). В узлах этого гра­фа обозначаются состояния системы (исходы полета); вершина графа (состояние 0) соответствует нормальной ситуации. Сос­тояния системы, в которые она переходит непосредственно из нулевого состояния вследствие появления опасных факторов, 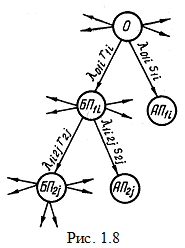на­зываются состояниями первого уровня, а состояния, возникающие из состояний первого уровня, – состояниями второго уровня и т. д.

Обозначим эти состояния: на первом уровне по i-му фак­тору – 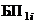, 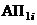– соответственно для благополучных и неб­лагополучных исходов; на втором уровне по j-му фактору – 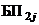, 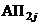и т.д. На стрелках графа проставляются интенсив­ности перехода от одного состояния к другому: при переходе от нулевого состояния к состояниям первого уровня – 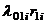; ; 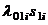при переходе от состояний первого уровня к состояниям второго уровня – 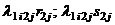и т.д.

Дифференциальные уравнения для определения неизвестных вероятностей состояний составляют по определенному правилу:

число уравнений равно числу состояний (исходов), размечен­ных на графе;

в левой части уравнения стоит производная вероятности дан­ного состояния, а правая часть содержит столько членов, сколько стрелок связано с данным состоянием;

если стрелка выходит из этого состояния, то соответствующий член уравнения имеет знак «минус», если она направлена в состояние – «плюс»;

каждый член уравнения равен произведению интенсивности перехода, соответствующей данной стрелке, на вероятность того состоя­ния, из которого стрелка исходит.

Для краткости обозначим суммарные интенсивности исходов из соответствующих состояний 0, 1i, 2j через

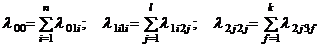. (1.32)

В (1.32) 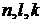– числа факторов, которые могут вывести систему соответственно из нулевого состояния, из i-го состоя­ния первого уровня, из j-го состояния второго уровня. Соот­ношения (1.32) учитывают, что .

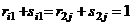Воспользовавшись указанным выше правилом, составим диф­ференциальные уравнения для вероятностей состояний, соответ­ствующих графу на рис. 1.7:

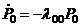; (1.33)

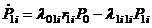; (1.34)

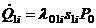; (1.35)

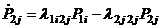; (1.36)

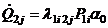. (1.37)

Система дифференциальных уравнений (1.33) – (1.37) ре­шается при следующих начальных условиях:

, , .

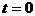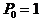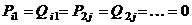В первую очередь решается уравнение для вероятности ну­левого состояния; затем, используя этот результат, произво­дится решение уравнений для вероятностей состояний первого уровня и т.д. Для оценки безопасности полета достаточно ре­шить только уравнения для вероятностей благополучных исхо­дов, но для проверки правильности решения по условию 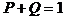необходимо решать всю систему дифференциальных уравнений.

Оценка БзП с учетом состояний только первого уровня. Сложность графа состояний и число возможных уровней состоя­ний, которые необходимо учитывать при оценке безопасности полета, определяются характером рассматриваемой задачи. В частности, для состояний, связанных с отказами резервирован­ных систем, граф состояний должен иметь как минимум два–три уровня.

Наибольшее влияние на уровень БзП оказывают состояния первого уровня, так как они вызваны появлением в полете од­ного опасного фактора, в то время как состояния второго уровня обусловлены последовательным появлением двух факто­ров, третьего уровня – трех и т.д. Соответственно и вероят­ности состояний от уровня к уровню убывают, поэтому в ряде случаев граф состояний можно ограничить первым уровнем. Это равносильно допущению о том, что за рассматриваемое время полета более одного опасного фактора не возникает. Неизвес­тные вероятности состояний , , 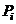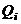при этом опреде­ляются из решения уравнений (1.33) – (1.35) при условии (в дальнейшем индексы 0 и 1 при решении уравнений можно опустить).

Решая эти уравнения, получим

;

.

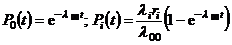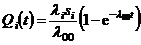На основании этих решений выражения для вероятностей благополучного и неблагополучного исходов полета примут вид:

; (1.38)

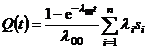. (1.39)

Как следует из выражения (1.39), удельный вклад i-го фактора в уровень аварийности равен :

.

По этому критерию можно определить факторы, оказывающие наи­более отрицательное влияние на БзП. Как частный случай для одного опасного фактора (n = 1) показатели БзП принимают вид:

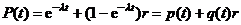; (1.40)

. (1.41)

Видно, что выражения (1.40) и (1.41) идентичны соответ­ственно выражениям (1.13) и (1.14).

Оценка БзП с учетом этапности выполнения полета. С уче­том этапности полета при решении дифференциальных уравнений (1.33) – (1.37) нужно учитывать следующее:

1. Каждый s-й из z этапов полета занимает определенную продолжительность по времени. За начало отсчета времени каж­дого этапа полета будем принимать 0, а за конец t. При этом , где , – текущее время полета, отсчитываемое от начала полета до конца предыдущего этапа и конца исследуемого этапа.

2. Начальные условия при решении дифференциальных уравне­ний, описывающих марковский процесс смены состояний на рас­сматриваемом s-м этапе, являются вероятностями соответствую­щих состояний в конце предыдущего 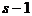-го этапа полета.

Ограничивая граф состояний состояниями первого уровня, запишем дифференциальные уравнения относительно неизвестных вероятностей состояний для s-го этапа полета:

; (1.42)

; (1.43)

. (1.44)

Решение системы уравнений (1.42) – (1.44) при начальных усло­виях 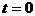; ; ; имеет вид:

; (1.45)

; (1.46)

. (1.47)

Показатели безопасности для s-го этапа на основании (1.45) – (1.47) запишутся в виде

; (1.48)

. (1.49)

В целом для полета

; (1.50)

. (1.51)

Условие нормировки выполняется.

Пример. Рассчитать зависимость по этапам полета с учетом отказов функциональной системы непрерывного дей­ствия по марковской модели. Исходные данные имеют гипотети­ческий характер и представлены в табл. 1.2.

Т а б л и ц а 1.2

№	№ п/п этапа
отк.	l,ч	t эт,ч	0,06	0,07	1,16	0,08	0,13
	0,010	s	0,019	0,015	0,009	0,020	0,035
	0,001	0,075	0,060	0,004	0,070	0,057
	0,015	0,011	0,009	0,006	0,015	0,023
	0,023	0,009	0,007	0,005	0,001	0,033
	0,015	0,013	0,011	0,007	0,019	0,015
	0,037	0,015	0,009	0,0025	0,0078	0,019

Как показывают проведенные исследования, при расчетах показателей безопасности полетов в большинстве случаев дос­таточно учесть возможность последовательного появления в по­лете только двух опасных факторов в любых их комбинациях. Расчетные соотношения для показателей БзП при ограничении графа состояний двумя уровнями читатель при соответствующих навыках решения дифференциальных уравнений (1.33) – (1.37) мо­жет получить самостоятельно. Для сравнения расчеты в данном примере выполнены с учетом двух возможных отказов функциональной системы и одного отказа.

Анализ результатов расчета , представленных на рис. 1.9, показывает:

от этапа к этапу разница в значениях , полученных с учетом двух отказов и одного отказа, возрастает;

на отдельном непродолжительном (порядка 0,5 ч) участке по­лета при расчете достаточно ограничиться учетом только одного отказа (в общем случае – опасного фактора), относительная разница с учетом двух и одного отка­зов не превышает при этом 5%.

В заключение этого параграфа отметим, что в нем была рассмотрена методика расчета показателей безопасности поле­та на основе представления смены состояний системы в полете однородным марковским процессом, то есть когда . Если интенсивность переходов – функция времени, то есть , то марковский процесс является неоднородным и описывается системой дифференциальных уравнений с переменны­ми коэффициентами. В остальном же методика расчета показате­лей безопасности полета остается прежней.

Задачи,