С помощью вероятностных показателей

Авиационное происшествие – случайное событие. Оно может произойти при условии, что в полете появится опасный фак­тор (группа факторов) и его последствия не будут парированы экипажем (летчиком). Опасные факторы, являясь следствием вполне конкретных причин, возникают в произвольные моменты времени, и в этом заключается их случайность.

За событие парирования примем событие невыхода опреде­ляющих параметров за свои предельные значения . Строго говоря, событие не всегда обязательно приводит к АП. В ряде случаев после превышения летчик своими действиями может возвратить ЛА в область , например, парировать режим сваливания самолета и возвратить его на нормальные углы атаки. В дальнейшем для однозначности суждений выход одного или нескольких опреде­ляющих параметров за их предельные значения будем полагать за неблагоприятный исход полета (АП).

Обозначим: , – вероятности непоявления и появления -го опасного фактора; , – условные вероятности парирования и непарирования его последствий. В принятых обозначениях, учитывая, что , , вероятнос­тные показатели БзП будут иметь очевидные выражения

(1.13)

(1.14)

Формула (1.13) имеет простой физический смысл, который мож­но интерпретировать следующим образом: по отношению к i-му опасному фактору полет с вероятностью 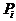будет безопасным, если i-й фактор с вероятностью не проявится, а если и проявится с вероятностью , то его последствия с условной вероятностью будут парированы экипажем (летчиком). По аналогии читатель может раскрыть смысл формулы (1.14).

Сложнее обстоит вопрос получения развернутых выражений для 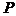и с учетом возможного воздействия на ЛА в поле­те совокупности опасных факторов.

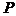Задача определения аналитической зависимости уровня риска (или вероятности ) в течение времени полета 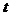с учетом всех свойств авиационной системы и внешней среды, по­тенциально влияющих на БзП, является ключевой в теории безо­пасности полетов и до настоящего времени в конечном виде не решена. Сложность решения этой задачи заключается в том, что, во-первых, свойства авиационной системы и внешней сре­ды представляются обширным множеством физически разнородных параметров, что приводит к большой размерности решаемой за­дачи; во-вторых, не все свойства авиационной системы, отри­цательно влияющие на БзП, выявлены достаточно четко; в-третьих, отдельные свойства авиационной системы и внешней среды не могут быть формализованно представлены набором опреде­ленных параметров, являющихся статистически контролируемы­ми. По поводу последнего можно привести такой пример: извес­тно, что возможность столкновения самолета с птицами влияет на уровень риска, однако рассчитать вероятность этого события в общем случае не представляется возможным. Можно лишь ука­зать на периоды времени или режимы полета, где столкновение наиболее вероятно.

По указанным выше причинам задача определения аналити­ческой зависимости уровня риска от времени полета решает­ся только в частных случаях для отдельных совокупностей опасных факторов. Методика расчета 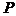и при этом зависит от специфики опасных факторов и их последствий. Эта специ­фика может быть отображена набором признаков, показанных на рис. 1.5.

Вероятность появления дискретных во времени факторов не зависит от времени полета, а определяется в основном харак­тером выполняемого этапа полета, уровнем подготовки летчика. К таким факторам можно, например, отнести отказы дискретно функционирующих систем ЛА, ошибки в технике пилотирования при выполнении сложного маневра. Вероятность появления неп­рерывных по времени факторов является функцией времени поле­та. К таким факторам можно отнести отказы непрерывно фун­кционирующих систем ЛА, ошибки летчика в технике пилотирова­ния при выполнении стационарных режимов полета, выбросы пе­регрузки из-за воздействия турбулентности и др. Однократно появляющиеся факторы могут возникать в полете только один раз, многократно появляющиеся факторы в полете могут повто­ряться несколько раз при условии, если предыдущее появление фактора парировано экипажем.

Независимые факторы могут появляться в полете в любой последовательности, зависимые – в такой последовательности, которая определяется зависимостью факторов друг от друга. Последствия факторов можно считать независимыми, если они не зависят от того, в какой последовательности факторы появ­ляются в полете, и зависимыми – в противном случае. Приме­ром последних могут быть отказы в системе САУ–блок контро­ля. Если САУ отказывает при работающем блоке контроля, то ее отказы, как правило, не опасны; если САУ отказывает при уже отказавшем блоке контроля, то ее отказы могут быть опасны­ми.

Математическим формулировкам методов расчета показате­ле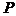й и , изложенным в параграфах 1.5 и 1.6, предпишем сле­дующие исходные положения:

1. Для исследуемого случая расчета показателе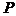й и возможно возникновение в полете n опасных факторов.

2. Полет продолжительностью 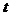состоит из 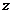последовательно (в соответствии с заданием) выполняемых этапов (1, 2,..., ,..., ).

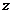3. Величина условной вероятности парирования последствий факторов зависит от этапа полета и изменяется от этапа к этапу ступенчато.

4. Считаются известными для каждого 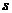-го этапа величины – соответственно вероятности невозникновения и возникновения -го фактора и условные вероят­ности его парирования и непарирования.

1.5. Определение вероятности

безопасного полета

Методом перебора гипотез

В основу математической формулировки метода может быть положена формула полной вероятности, предусматривающая рас­смотрение всех физически возможных гипотез, связанных с от­дельными опасными факторами и их комбинациями.

Вероятность благополучного исхода полета при n воз­можных опасных факторах в любых их сочетаниях можно запи­сать в виде

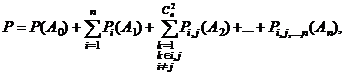(1.15)

где 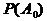– вероятность того, что не возникает ни один опасный фактор; 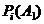, 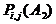– вероятность того, что возникают только один опасный фактор и исход полета будет благополучным, два опасных фактора и т.д.

Слагаемые в (1.15) при условии, что факторы независи­мы, определяются следующими выражениями:

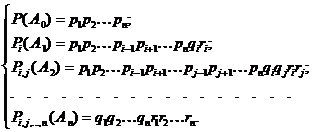(1.16)

Вероятность авиационного происшествия определяется из очевидного условия, что каждый последующий опасный фак­тор во время полета физически возможен, если перед этим опасные факторы не возникали, а если и возникали, то они парировались. В соответствии с этим условием получим

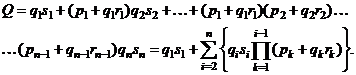(1.17)

Вообще говоря, уровень риска можно вычислить и более простым способом – как вероятность противоположного события, то есть

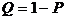. (1.18)

Рассмотрим элементарный пример. Определить выражение для 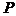при воздействии двух независимых факторов. В соответ­ствии с (1.15) и (1.16) имеем

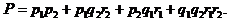(1.19)

Нетрудно заметить, что выражение (1.19) может быть представ­лено произведением

.

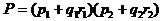Обобщая этот результат для n независимых факторов, полу­чим

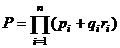. (1.20)

Формула (1.20) является компактной записью развернутых выра­жений, представленных (1.15) и (1.16).

С учетом воздействия на ЛА только одного фактора, кото­рый может возникать в полете неоднократно, например m раз, на основании (1.20) имеем

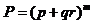. (1.21)

Учитывая, что 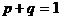, , 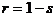из (1.21) следует

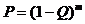, (1.22)

где 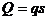– уровень риска при однократном появлении фактора.

Раскладывая функцию (1.22) в ряд и ограничиваясь первыми двумя членами разложения, получим

.

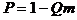Заметим, что это соответствует разложению функции 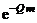при ограничении его первыми двумя членами разложения. Следова­тельно, приближенно можно представить

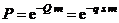. (1.23)

Пример. При выполнении маневра вероятность ошибки лет­чика 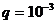, условная вероятность ее непарирования 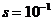. Оценить безопасность выполнения 100 таких манев­ров.

Расчеты проводим в соответствии с формулой (1.22):

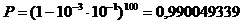
и формулой (1.23) :

.

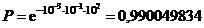Как видно, погрешность от замены точной формулы приближен­ной сказывается только начиная с седьмого знака после запя­той.

До сих пор все рассуждения и выкладки относительно ме­тодики расчета показателе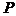й и велись без учета этапнос­ти выполнения полета. К решению этой задачи можно подойти, рассматривая вероятности благополучного 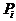и неблагополуч­ного 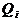исходов по каждому i-му фактору с учетом этапности выполнения полета.

Для фактора i-го типа последовательность событий по этапам полета, связанная с возможностью его появления на од­ном из этапов, может быть представлена графом (деревом состояний), изображенным на рис. 1.6. Граф характеризует многошаговый процесс (1,..., 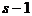, ,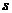..., 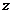) перехода системы из од­ного состояния (события) к другому с учетом возможности появления i-го фактора на рассматриваемом этапе, начиная от первого и заканчивая последним. На стрелках графа простав­ляются вероятности перехода от одного состояния к другому, при этом должно соблюдаться условие: сумма вероятностей на всех стрелках, выходящих из одного состояния, должна рав­няться единице.

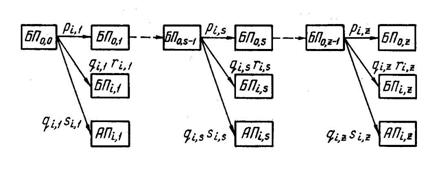
Рис. 1.6

На рис. 1.6 обозначено: 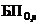– событие непоявления i-го фактора на s-м этапе; 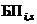, 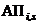– события благополучного и неблагополучного исхо­дов при появлении i-го фактора на s-м этапе.

Вероятности этих событий определяются как произведение всех вероятностей, указанных на стрелках, начиная от рас­сматриваемого события и заканчивая начальным 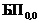. Заметим, что вероятность 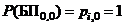, то есть в начале полета i-й фактор отсутствует.

В соответствии с изложенным

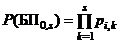; (1.24)

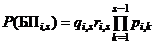; (1.25)

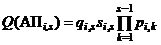. (1.26)

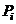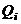Для всех z этапов полета показатели и с учетом воздействия только одного i-го фактора на основании формул (1.24) – (1.26) приобретают вид:

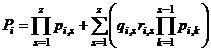; (1.27)

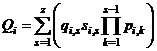. (1.28)

По всем n факторам, учитывая их независимость, имеем

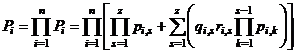. (1.29)

Уровень риска за полет с учетом возможного воздействия всех n факторов определим как

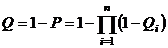. (1.30)

Раскрывая почленно произведение 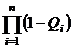, на основании формулы (1.30) определяем

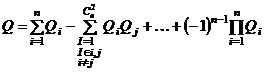. (1.31)

Условие нормировки 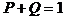выполняется. Учитывая, что 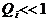, в ряде случаев формулу (1.31) можно ограничить только первым слагаемым, то есть

.

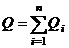В заключение укажем, что метод перебора гипотез при расчете показателе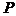й и может применяться как для дис­кретных, так и непрерывных факторов, как зависимых, так и независимых.

При расчете показателе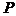й и для зависимых факторов целесообразно пользоваться графической интерпретацией пере­хода системы от одного состояния (события) к другому, так как умозрительный перебор всех гипотез, связанных с появле­нием отдельных факторов и их комбинаций, затруднен. Граф (де­рево состояний) должен строиться по правилам, реализованным при построении графа, показанного на рис. 1.6.

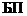В качестве примера рассмотрим случай воздействия двух зависимых факторов: второй фактор может появиться при условии, если первый уже появился. Граф для этого случая указан на рис. 1.7. Как видно из него, сложные события и 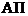представляются суммами событий: ; .

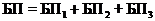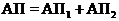Вероятности элементарных событий равны:

.

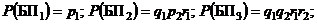
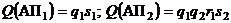Отсюда .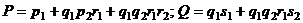

В правильности выкладок читатель может убедиться по условию

.
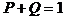