Разработка математической модели
Введем обозначения:
n - количество поставщиков:
m- количество потребителей:
i-номер строки, поставщика. 1,2, …,n;
j- номер столбца, потребителя, 1,2,...m;
Xij- искомое плановое количество перевозки от i-гo поставщика к j-му потребителю;
Si - план поставок oт i-гo поставщика всем потребителям, сумма по строке;
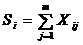
Cj- план поставок j-му потребителю от всех поставщиков, сумма по столбцу;
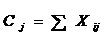
Рij - стоимость перевозки единицы груза от i-го поставщика к j-му потребителю;
Bi - ограниченная мощность i-гo поставщика;
Dj- ограниченный спрос j-гo потребителя.
В общем виде экономико-математическая модель постановки задачи будет выглядеть следующим образом: минимизировать затраты на перевозку грузов (целевая функция)
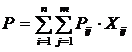
при ограничениях Si<=Bi, Cj>=Dj и неотрицательных объемах перевозок Xj>=0.
Для решения данной задачи можно использовать симплексный метод, метод потенциалов и др.
Формулы табличной модели
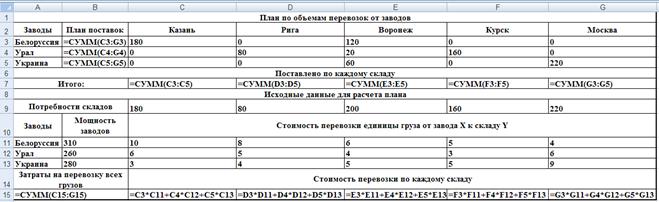
После составления плановой таблицы необходимо связать показатели формулами для вычислений. Представление формул и чисел исходных данных дано в таблице
Поиск оптимального плана
Скопировать в буфер обмена исходную таблицу 1, открыть Лист 2 и вставить из буфера обмена таблицу 1. Переименовать Лист 2 в «Оптимальный план». Лист 1 назвать «Исходные данные»
1. Выполнить команду меню Данные → Поиск решения.
2. В появившемся диалоговом окне Поиск решения выполнить настройку модели (математическая постановка задачи для оптимизации):
· В поле целевой ячейки ввести ее адрес А15.
· В поле Ограничения ввести 3 строки неравенств значений диапазонов: поставки от заводов не должны превышать мощности заводов, поставки потребителям не должны быть меньше потребностей, значения плана не могут быть отрицательными.
Свод параметров модели дан в таблице
| Параметр задачи | Ячейки | Семантика |
| Результат | А15 | Цель – уменьшение всех транспортных расходов |
| Изменяемые данные | C3:G5 | Объемы перевозок от каждого из заводов к каждому складу |
| Ограничения | B3:B5<=B11:B13 | Количество перевезенных грузов не может превышать производственных возможностей |
| C7:G7>=C9:G9 | Количество поставляемых грузов не должно быть меньше потребностей складов | |
| C3:G5>=0 | Число перевозок не может быть отрицательным |
3. После настройки модели и установки параметров алгоритма нажать кнопку Выполнить окна Поиск решения.
4. Проверьте, чтобы в полученном решении было m+n-1=7 не нулевых перевозок, где m - количество заводов, n – количество складов. В противном случае задача является вырожденной.
Задания для самостоятельного решения
Задание 1.
Пусть имеются S=4 поставщика и D=5 потребителей. Издержки перевозки единицы груза от i-го поставщика в j-й пункт назначения, запасы поставщиков и заказы потребителей приведены в таблице.
| D1 | D2 | D3 | D4 | D5 | Запасы | |
| S1 | ||||||
| S2 | ||||||
| S3 | ||||||
| S4 | ||||||
| Заказы |
Требуется оптимизировать план перевозок.
Задание 2
Пусть имеются производители продукции в городах Курск, Калуга, Воронеж и Орел и торговые склады в городах Москва, Смоленск, Киров, Тверь. Издержки перевозки единицы груза от i-го производителя в j-й пункт назначения, запасы производителей и заказы потребителей приведены в таблице.
| Москва | Смоленск | Киров | Тверь | Запасы | |
| Курск | |||||
| Калуга | |||||
| Воронеж | |||||
| Орел | |||||
| Заказы |
Требуется оптимизировать план перевозок.
Задание 3.
Имеется три поставщика с запасами товара и 3 потребителя данного товара. Требуется определить оптимальный план перевозок, при котором суммарные затраты на транспортировку грузов будут минимальны. Сведения о возможностях поставщиков и запросах потребителей, а также цены на перевозку единицы товара от поставщиков к потребителям сведены в таблицу.
| Потребители Поставщики | D1=41 | D2=49 | D3=40 |
| S1=61 | |||
| S2=39 | |||
| S3=56 |
Составить экономико-математическую модель решения задачи, учитывая, что:
Si – возможности i-го поставщика в условных единицах;
Di – потребности j-го потребителя в тех же единицах;
xij – объем планируемых перевозок.
Задание 4.
Привести открытую транспортную задачу, представленную в таблице, к закрытой. Составить экономико-математическую модель, оптимизирующую план перевозок.
| Поставщики | Мощности поставщиков | Потребители и их спрос | |||
Задание 5.
Пусть требуется минимизировать затраты на перевозку товаров от 3 предприятий-производителей на торговые склады 5 городов, куда необходимо поставить 180, 80, 200, 160 и 220 единиц товара соответственно. При этом необходимо учесть возможности поставок каждого из производителей при максимальном удовлетворении запросов потребителей и затраты на перевозку единицы товара.
| Заводы: | Поставки | Склад 1 | Склад 2 | Склад 3 | Склад 4 | Склад 5 |
| I | ||||||
| II | ||||||
| III |
Задание 6.
Привести открытую транспортную задачу, представленную в таблице, к закрытой. Составить экономико-математическую модель, оптимизирующую план перевозок.
| Поставщики | Мощности поставщиков | Потребители и их спрос | |||
Задание 7.
Привести открытую транспортную задачу, представленную в таблице, к закрытой. Составить экономико-математическую модель, оптимизирующую план перевозок.
| Поставщики | Мощности поставщиков | Потребители и их спрос | ||
Контрольные вопросы для допуска и защиты работы
1. Каково назначение программы-надстройки "Поиск решения"?
2. Как установить надстройку Поиск решения
3. Перечислите основные элементы оптимизационной математической модели.
4. Опишите возможный порядок построения оптимизационной модели.
5. Пояснить структуру плановой таблицы.
6. Перечислить исходные данные, переменные и результирующие показатели модели.
7. Дать краткую технологию решения транспортной задачи в программе Excel Поиск решения.
