Информационная технология поиска решения

Microsoft Excel обеспечивает решение задач линейного и нелинейного программирования ограниченной размерности. Для реализации оптимизационных расчетов в Microsoft Excel необходимо установить надстройку Поиск решения с помощью команды меню Данные ► Работа с данными ► Настройка панели быстрого доступа ► Надстройки ► Перейти ► Поиск решения, и правильно подготовить данные оптимизационной модели на листе. Модель задачи задается в диалоговом окне Поиск решения. Модель использует целевую функцию, которая записывается в виде формулы в отдельной ячейке. Для целевой функции указывается: максимизация, минимизация или равенство фиксированному значению. В процессе поиска решения изменяются значения в указанных ячейках, соответствующих переменным, при соблюдении ограничений.

Дополнительные настройки оптимизации выполняются в диалоговом окне Параметр поиска решения. В частности, можно ограничить время выполнения поиска решения и выполнения промежуточных вычислений, максимальное время — не более 9 часов, точность, с которой найденное решение соответствует целевому значению, допустимое отклонение для переменных от оптимального значения. Для задач с нелинейной целевой функцией задается параметр сходимости, который влияет на прекращение поиска. Если относительные изменения значения целевой функции за последние пять итераций меньше указанного числа, поиск прекращается. Выполняется установка типа модели — линейная, если целевая функция линейная. Можно выводить результаты итераций, выполнять автоматическое масштабирование параметров модели.

При решении задачи можно выбрать метод экстраполяции оценокпеременных для каждого шага поиска — линейная или квадратичная (для задач с нелинейной целевой функцией), метод численного дифференцирования для целевой функции — прямые или центральные разности (для задач с нелинейной целевой функцией), метод поиска — метод Ньютона (требуется много оперативной памяти) или метод сопряженных градиентов (больше итераций). Основным ограничением модели является максимальное число переменных — 200. Несколько оптимизационных моделей на одном листе можно сохранять и загружать по мере необходимости.

Если решение найдено, его можно сохранить либо восстановить исходные значения переменных. Результат решения можно сохранить в качестве сценария.

По результатам решения создаются отчеты. Отчет по результатам — сведения о целевой функции с указанием ячейки, исходного и конечного значения, сведения о переменных с указанием списка ячеек, исходных и конечных значений, сведения об ограничениях с указанием списка ячеек, формул, вычисленных значений и статуса и разницы (свободного остатка). Отчет по устойчивости — сведения о чувствительности модели (изменение целевой функции при изменении переменных и ограничений). Отчет по пределам — сведения о нижних и верхних границах значений переменных. Нижний предел — наименьшее значение переменной, верхний предел — наибольшее значение переменной (значения всех прочих переменных фиксированы и удовлетворяют ограничениям).

Постановка задачи:

Требуется минимизировать затраты на перевозку товаров от предприятий-производителей на торговые склады. При этом необходимо учесть возможности поставок каждою из производителей при максимальном удовлетворении запросов потребителей. В этой модели представлена задача доставки товаров с 3 заводов к 5 региональным потребителям. Товары могут доставляться с любого завода к любому потребителю, однако стоимость доставки на большее расстояние будет большей.

Необходимо определить объемы перевозок между каждым заводом и потребителем в соответствии с потребностями складов и производственными мощностями заводов, при которых транспортные расходы минимальны.

Задание

Разработка табличной модели

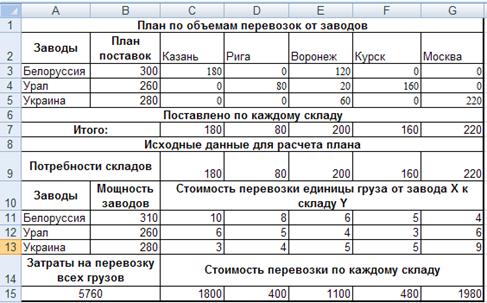
В верхней строке электронной таблицы Excel даны имена колонок A,B,C и т.д. В первой колонке номера строк. В колонке А - имена заводов-поставщиков. В строке 2 - имена потребителей.

Общие плановые затраты в ячейке АI5 надо минимизировать. Искомая плановая матрица объемов перевозки грузов от каждого поставщика к каждому потребителю расположена в диапазоне СЗ:G5.

В диапазоне ВЗ:В5 вычисляются планы поставок от каждого завода всем потребителям как суммы по строкам. Необходимо, чтобы эти суммы не превысили мощностей заводов-поставщиков. В строке 7 вычисляются планы поставок каждому потребителю от всех заводов как суммы по столбцам. Необходимо, чтобы эти суммы были равны или не меньше заказов потребителей.

В строках 9, 11:13 представлены исходные данные для расчетов. В диапазон В11:В13 вводятся мощности заводов-поставщиков. В матрицу C11:G13 надо ввести стоимость перевозки единицы груза от каждого поставщика к каждому потребителю. В строку 9 вводятся плановые потребности складов.

В строке 15 вычисляются стоимость перевозок для каждого склада и общие затраты по транспортировке.