Основные задачи аналитической геометрии на плоскости.
В аналитической геометрии на плоскости возникают две основные задачи. Первая: зная геометрические свойства кривой, найти ее уравнение; вторая: зная уравнение кривой изучить ее форму и свойства.
На рисунках 32-40 приведены примеры некоторых кривых и указаны их уравнения.
| О |
| R |
| p |
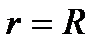 |
| О |
| 2R |
| p |
| r |
| φ |
| О |
| 2R |
| p |
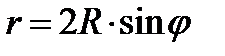 |
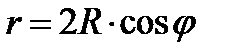 |
| r |
| φ |
| О |
| R |
| R |
| y |
| x |
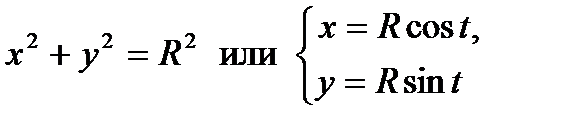 |
| О |
| R |
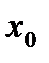 |
| y |
| x |
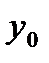 |
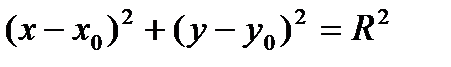 |
| Рис. 32. Окружность радиуса R |
I zUvOT8nMS7dVCg1x07VQUiguScxLSczJz0u1VapMLVayt+PlAgAAAP//AwBQSwMEFAAGAAgAAAAh AAI2fLTCAAAA3QAAAA8AAABkcnMvZG93bnJldi54bWxET0uLwjAQvi/4H8II3tbUHlSqUUR8HdwF H3gemrEtNpPSpLb+eyMs7G0+vufMl50pxZNqV1hWMBpGIIhTqwvOFFwv2+8pCOeRNZaWScGLHCwX va85Jtq2fKLn2WcihLBLUEHufZVI6dKcDLqhrYgDd7e1QR9gnUldYxvCTSnjKBpLgwWHhhwrWueU Ps6NUbBp4rj9uY2ro97dH/sTN+1t+qvUoN+tZiA8df5f/Oc+6DB/NJnA55twgly8AQAA//8DAFBL AQItABQABgAIAAAAIQAEqzleAAEAAOYBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBl c10ueG1sUEsBAi0AFAAGAAgAAAAhAAjDGKTUAAAAkwEAAAsAAAAAAAAAAAAAAAAAMQEAAF9yZWxz Ly5yZWxzUEsBAi0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABIAAAAAAAAAAAAAAAAALgIAAGRycy9w aWN0dXJleG1sLnhtbFBLAQItABQABgAIAAAAIQACNny0wgAAAN0AAAAPAAAAAAAAAAAAAAAAAJ8C AABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABAD3AAAAjgMAAAAA "> 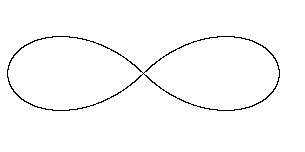
| О |
| p |
| a |
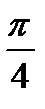 |
Рис. 33. Лемниската Бернулли Уравнение в прямоугольных координатах: 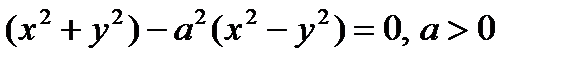 ; в полярных координатах: ; в полярных координатах: 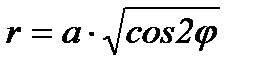 . . |

| p |
| О |
| a |
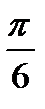 |
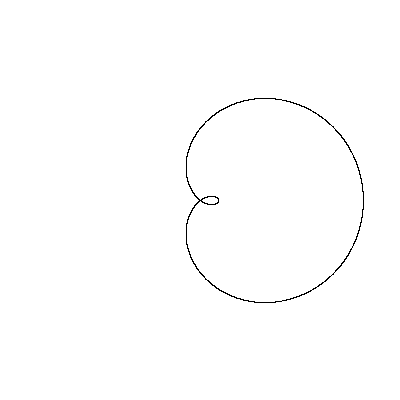
Рис.34. Трехлепестковая роза В полярных координатах ее уравнение имеет вид: 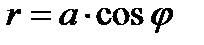 , где , где 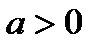 . . |
| О |
| p |
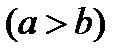 |
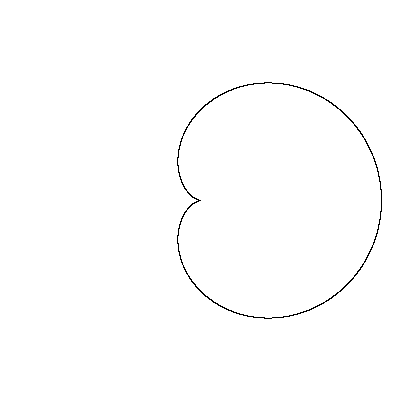
| p |
| О |
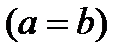 |
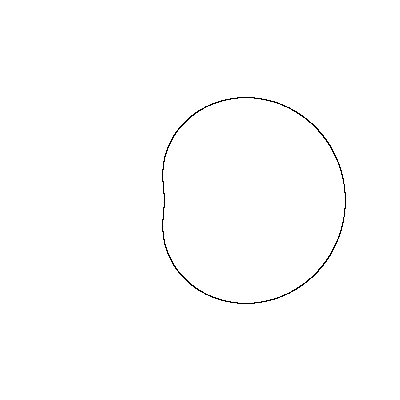
| О |
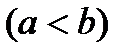 |
| p |
Рис. 35. Улитка Паскаля Уравнение в полярных координатах имеет вид: 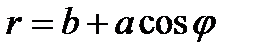 |
| x |
| y |
| O |
| x |
| y |
| O |
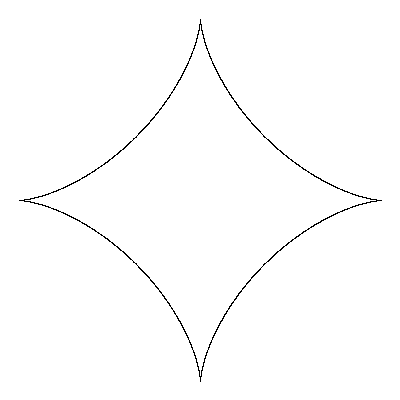
Рис. 36. Полукубическая парабола Уравнение кривой 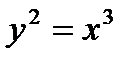 или или 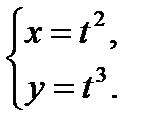 |
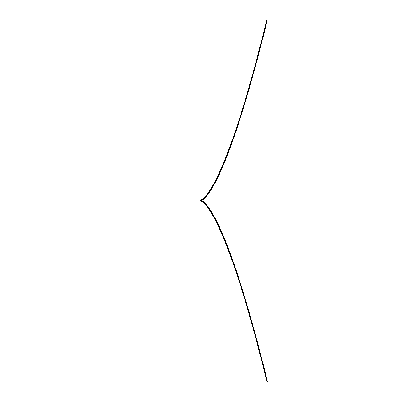
Рис. 37. Астроида Уравнение в прямоугольных координатах: 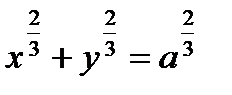 ; параметрические уравнения: ; параметрические уравнения: 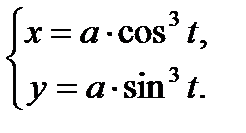 |

| p |
| О |
| r |
| 2a |
| φ |
| О |
| 2π |
| 2π |
| p |
Рис. 38. Кардиоида Уравнение в полярных координатах имеет вид 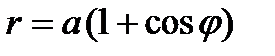 , где , где 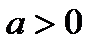 . Кардиоида – частный случай улитки Паскаля . Кардиоида – частный случай улитки Паскаля 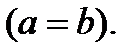 |
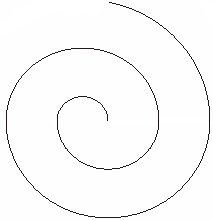
Рис. 39. Спираль Архимеда Уравнение кривой в полярных координатах 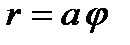 , где , где 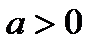 – постоянное – постоянное |
I zUvOT8nMS7dVCg1x07VQUiguScxLSczJz0u1VapMLVayt+PlAgAAAP//AwBQSwMEFAAGAAgAAAAh AB2BnGTEAAAA3AAAAA8AAABkcnMvZG93bnJldi54bWxEj0FrAjEUhO9C/0N4Qm+aVbCuq1GsIAi9 VGvF42PzTBY3L8sm6vbfN4WCx2FmvmEWq87V4k5tqDwrGA0zEMSl1xUbBcev7SAHESKyxtozKfih AKvlS2+BhfYP3tP9EI1IEA4FKrAxNoWUobTkMAx9Q5y8i28dxiRbI3WLjwR3tRxn2Zt0WHFasNjQ xlJ5Pdycgg8zCafcbG67c/Zt7XFsPqv3tVKv/W49BxGpi8/wf3unFeSzKfydSUdALn8BAAD//wMA UEsBAi0AFAAGAAgAAAAhAASrOV4AAQAA5gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5 cGVzXS54bWxQSwECLQAUAAYACAAAACEACMMYpNQAAACTAQAACwAAAAAAAAAAAAAAAAAxAQAAX3Jl bHMvLnJlbHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEgAAAAAAAAAAAAAAAAAuAgAAZHJz L3BpY3R1cmV4bWwueG1sUEsBAi0AFAAGAAgAAAAhAB2BnGTEAAAA3AAAAA8AAAAAAAAAAAAAAAAA nwIAAGRycy9kb3ducmV2LnhtbFBLBQYAAAAABAAEAPcAAACQAwAAAAA= "> 


| О |
| x |
| y |
| 2a |
| 2πa |
Рис. 40. Циклоида Параметрические уравнения циклоиды имеют вид 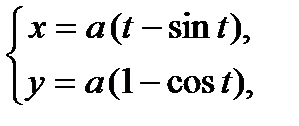 где где 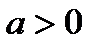 . Циклоида – это кривая, которую описывает фиксированная точка окружности, катящаяся без скольжения по неподвижной прямой . Циклоида – это кривая, которую описывает фиксированная точка окружности, катящаяся без скольжения по неподвижной прямой |
