Невырожденные матрицы. Обратная матрица.

Умножение на число

Произведением матрицы на число k называется матрица такая, что .

Пример 1.3.

, k = 2, .

Матрица называется противоположной матрице А.

Разность матриц А – В можно определить так: А – В = А + (-В).

Операции сложения матриц и умножения на число обладают следующими свойствами:

1. А + В = В + А;

2. А + (В + С) = (А + В) + С;

3. А + 0 = А;

4. А – А = 0;

5. 1 · А = А;

6. α · (А + В) = αА + αВ;

7. (α + β) · А = αА + βА;

8. α · (βА) = (αβ) · А, гдеА, В, С – матрицы, α и β – числа.

4. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду.

Элементарными преобразованиями матриц являются:

● перестановка местами двух параллельных рядов матрицы;

● умножение всех элементов ряда матрицы на число, отличное от нуля;

● прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицыАи В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. ЗаписываетсяА ~ В.

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например

.

Пример 1.4. Привести к каноническому виду матрицу

.

Решение: Выполняя элементарные преобразования, получаем

-2

-3

-5

~ ~ ~

:5

:2

:3

~ ~ ~

-1

~ ~ .

Невырожденные матрицы. Обратная матрица.

Основные понятия

ПустьА – квадратная матрица n-го порядка

.

Квадратная матрицаА называется невырожденной, если определитель не равен нулю: . В противном случае ( ) матрицаА называется вырожденной.

Матрицей, союзнойк матрицеА, называется матрица

,

где - алгебраическое дополнение элемента данной матрицыА (оно определяется так же, как и алгебраическое дополнение элемента определителя).

Матрица называется обратной матрицеА, если выполняется условие:

, (3.1)

гдеЕ – единичная матрица того же порядка, что и матрица А. Матрица имеет те же размеры, что и матрица А.

Обратная матрица

Теорема 3.1.Всякая невырожденная матрица имеет обратную.

Приведем доказательство для случая матрицы 3-го порядка. Пусть

, причем .

Составим союзную матрицу

и найдем произведение матриц :

т.е.

(3.2)

Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2).

Аналогично убеждаемся, что

. (3.3)

Равенства (3.2) и (3.3) перепишем в виде

и

Сравнивая полученные результаты с определением (3.1), получим

т.е. .

Отметим свойства обратной матрицы:

1. ;

2. ;

3. .

Алгоритм нахождения обратной матрицы

Пример 3.1. Найти , если

Решение: 1) Находим

2) Находим , поэтому

.

3) Находим .

Проверка:

.

Пример 3.2. Определить, при каких значениях λ существует матрица, обратная данной:

Решение: Всякая невырожденная матрицы имеет обратную. Найдем определитель матрицыА:

Если , т.е. , то , то матрицаА невырожденная, имеет обратную.

Пример 3.3. Показать, что матрица А является обратной дляВ, если

, .

Решение: Найдем произведение матрицАи В:

АналогичноВ · А = Е. Следовательно, матрица А является обратной для B

Определители 2-го и 3-го порядка. Основные понятия.

Основные понятия

Квадратной матрицеА порядка n можно сопоставить число detA (или |A|, или Δ), называемое ее определителем следующим образом:

1. n = 1. А = ; .

2. n = 2. ; .

3. n= 3. ;

.

Определитель матрицыА также называют его детерминантом. Правило вычисления детерминанта матрицы порядка N является довольно сложным для восприятия и применения. Однако, известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство определителей 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.

Вычисление определителя 2-го порядка иллюстрируется схемой:

.

Пример 2.1. Найти определители матриц

и .

Решение:

;

.

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:

.

(основания равнобедренных треугольников параллельны главной диагонали)

(основания равнобедренных треугольников параллельны побочной диагонали)

Пример 2.2. Вычислить определитель матрицы

.

Решение:

.

Системы линейных уравнений . Основные понятия.

Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида

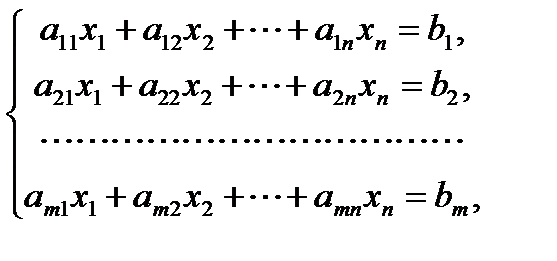
где числа 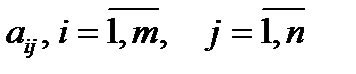называются коэффициентами системы, числа 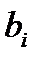– свободными членами. Подлежат нахождению числа .

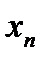Такую систему удобно записывать в компактной матричной форме

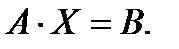ЗдесьА – матрица коэффициентов системы, называемая основной матрицей:

,

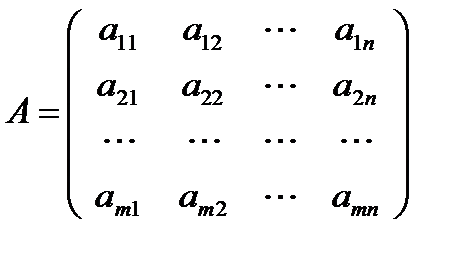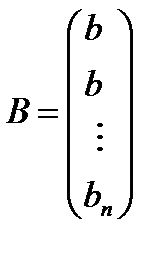
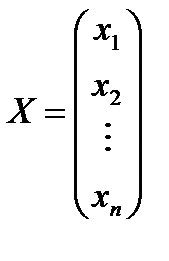– вектор-столбец из неизвестных ,

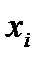– вектор-столбец из свободных членов .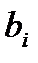

Произведение матриц 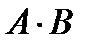определено, так как в матрицеА столбцов столько же, сколько строк в матрице Х (n штук).

Расширенной матрицей системы называется матрица 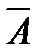системы, дополненная столбцом свободных членов

.

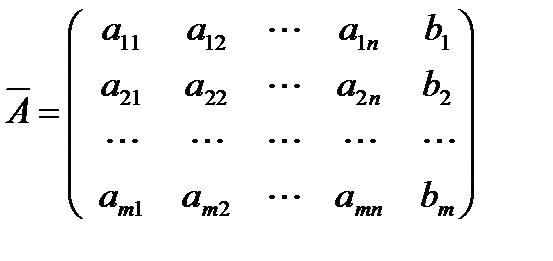Решением системы называется n значений неизвестных 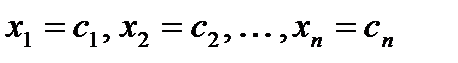, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы-столбца .

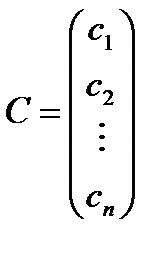Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она ни имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.

Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.

Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются только над строками матрицы.

Система линейных уравнений называется однородной, если все свободные члены равны нулю:

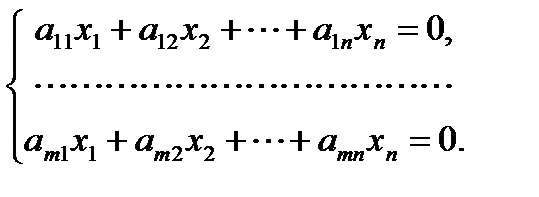
Однородная система всегда совместна, так как 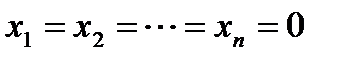является решением системы. Это решение называется нулевым или тривиальным.

Необходимость.

Так как ранг не может превосходить размера матрицы, то, очевидно, . Пусть . Тогда один из миноров размера отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то .

Достаточность.

Пусть . Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е. имеет и ненулевые решения.

Пусть дана однородная система линейных уравнений с неизвестными

Если система имеет ненулевые решения, то . Ибо при система имеет единственное, нулевое решение. Если же , то ранг основной матрицы системы меньше числа неизвестных, т.е. . И, значит, система имеет бесконечное множество (ненулевых) решений.

Теорема 4.4.Для того, чтобы система однородных уравнений с неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель был равен нулю, т.е. .

Пример 4.6. Решить систему

Решение: Так как , то система имеет бесчисленное множество решений. Найдем их

Стало быть – общее решение. Положив получим одно частное решение: Положив получаем второе частное решение: и т.д.

Векторы. Основные понятия.

Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.

Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина изображается с помощью вектора.

Вектор­– это направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. ЕслиА – начало вектора, а В – его конец, то вектор обозначается символом или . Вектор (у него начало в точке В, а конец в точке А) называется противоположным вектору . Вектор, противоположный вектору , обозначается .

Длиной или модулем вектора называется длина отрезка и обозначается . Вектор, дина которого равна нулю, называется нулевым вектором и обозначается . Нулевой вектор направления не имеет.

Вектор, длина которого равна единице, называется единичным вектором и обозначается через . Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается .

Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают || .

Коллинеарные векторы могут быть направлены одинаково или противоположно.

Нулевой вектор считается коллинеарным любому вектору.

Рис. 1.

Два вектора и называются равными ( = ), если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точкуО пространства.

На рисунке 1 векторы образуют прямоугольник. Справедливо равенство = , но . Векторы и – противоположные, . Равные векторы также называют свободными.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любых коллинеарны, то такие векторы компланарны.

Общее уравнение прямой

Рассмотрим уравнение первой степени относительно х и у в общем виде

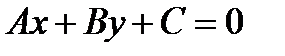, (10.4)

гдеА, В, С – произвольные числа, причем А и В не равны нулю одновременно.

Покажем, что уравнение (10.4) есть уравнение прямой линии. Возможны два случая.

ЕслиВ = 0, то уравнение (10.4) имеет вид 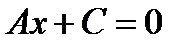, причем 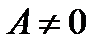, т.е. 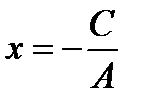. Это есть уравнение прямой, параллельной оси Оу и проходящей через точку .

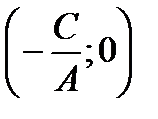Если 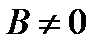, то из уравнения (10.4) получаем 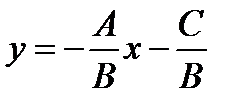. Это есть уравнение прямой с угловым коэффициентом .

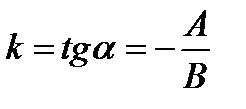Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой.

Некоторые частные случаи общего уравнения прямой:

1) еслиА = 0, то уравнение приводится к виду 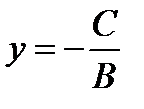. Это есть уравнение прямой, параллельной оси Ох;

2) еслиВ= 0, то прямая параллельна оси Оу;

3) еслиС= 0, то получаем 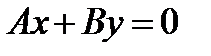. Уравнению удовлетворяют координаты точки 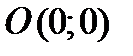, прямая проходит через начало координат.

Найдем уравнение прямой, проходящей через заданную точку 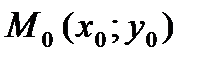перпендикулярно данному ненулевому вектору .

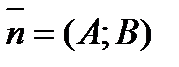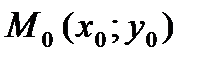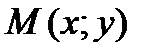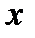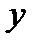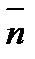Рис. 43.

Возьмем на прямой произвольную точку 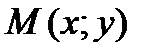и рассмотрим вектор 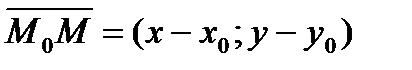(см. рис. 43). Поскольку векторы 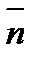и 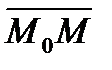перпендикулярны, то их скалярное произведение равно нулю: 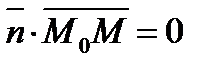, то есть

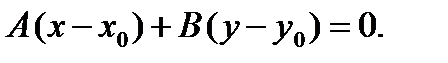(10.8)

Уравнение (10.8) называется уравнением прямой, проходящей через заданную точку перпендикулярно заданному вектору.

Вектор 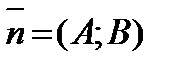, перпендикулярной прямой называется нормальным вектором этой прямой.

Уравнение (10.8) можно переписать в виде

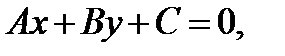(10.9)

гдеА и В – координаты нормального вектора, 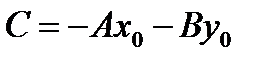– свободный член. Уравнение (10.9) есть общее уравнение прямой

Общее уравнение прямой

Рассмотрим уравнение первой степени относительно х и у в общем виде

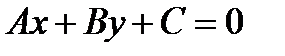, (10.4)

гдеА, В, С – произвольные числа, причем А и В не равны нулю одновременно.

Покажем, что уравнение (10.4) есть уравнение прямой линии. Возможны два случая.

ЕслиВ = 0, то уравнение (10.4) имеет вид 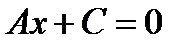, причем 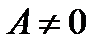, т.е. 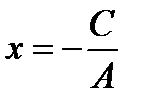. Это есть уравнение прямой, параллельной оси Оу и проходящей через точку .

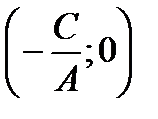Если 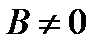, то из уравнения (10.4) получаем 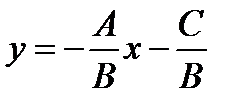. Это есть уравнение прямой с угловым коэффициентом .

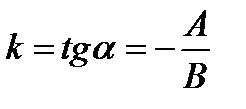Итак, уравнение (10.4) есть уравнение прямой линии, оно называется общим уравнением прямой.

Некоторые частные случаи общего уравнения прямой:

1) еслиА = 0, то уравнение приводится к виду 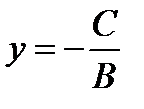. Это есть уравнение прямой, параллельной оси Ох;

2) еслиВ= 0, то прямая параллельна оси Оу;

3) еслиС= 0, то получаем 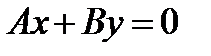. Уравнению удовлетворяют координаты точки 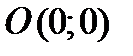, прямая проходит через начало координат.

Полярное уравнение прямой

Найдем уравнение прямой в полярных координатах. Ее положение можно определить, указав расстояние p от полюсаО до данной прямой и угол α между полярной осью l, проходящей через полюс О перпендикулярно данной прямой (см. рис. 44).

Для любой точки на данной прямой имеем:

Рис. 44.

О

α

φ

r

l

P

p

С другой стороны

Следовательно

(10.10)

Полученное уравнение (10.10) и есть уравнение прямой в полярных координатах.

Нормальное уравнение прямой

Пусть прямая определяется заданием p и α (см. рис. 45). Рассмотрим прямоугольную систему координат Оху. Введем полярную систему, взявО за полюс и Ох за полярную ось. Уравнение прямой можно записать в виде

т.е.

Но, в силу формул, связывающих прямоугольные и полярные координаты имеем: Следовательно, уравнение (10.10) прямой в прямоугольной системе координат примет вид

(10.11)

Уравнение (10.11) называется нормальным уравнением прямой.

О

х

у

p

α

Рис. 45

Покажем, как привести уравнение (10.4) прямой к виду (10.11).

Умножим все члены уравнения (10.4) на некоторый множитель . Получим Это уравнение должно обратиться в (10.11). Следовательно, должны выполняться равенства: Из первых двух равенств находим , т.е. Множитель называется нормирующим множителем. Согласно третьему равенству знак нормирующего множителя противоположен знаку свободного членаС общего уравнения прямой.

Пример 10.2. Привести уравнение к нормальному виду.

Решение: Находим нормирующий множитель Умножая данное уравнение на , получим искомое нормальное уравнение прямой:

Умножение на число

Произведением матрицы на число k называется матрица такая, что .

Пример 1.3.

, k = 2, .

Матрица называется противоположной матрице А.

Разность матриц А – В можно определить так: А – В = А + (-В).

Операции сложения матриц и умножения на число обладают следующими свойствами:

1. А + В = В + А;

2. А + (В + С) = (А + В) + С;

3. А + 0 = А;

4. А – А = 0;

5. 1 · А = А;

6. α · (А + В) = αА + αВ;

7. (α + β) · А = αА + βА;

8. α · (βА) = (αβ) · А, гдеА, В, С – матрицы, α и β – числа.

4. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду.

Элементарными преобразованиями матриц являются:

● перестановка местами двух параллельных рядов матрицы;

● умножение всех элементов ряда матрицы на число, отличное от нуля;

● прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Две матрицыАи В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. ЗаписываетсяА ~ В.

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например

.

Пример 1.4. Привести к каноническому виду матрицу

.

Решение: Выполняя элементарные преобразования, получаем

-2

-3

-5

~ ~ ~

:5

:2

:3

~ ~ ~

-1

~ ~ .

Невырожденные матрицы. Обратная матрица.

Основные понятия

ПустьА – квадратная матрица n-го порядка

.

Квадратная матрицаА называется невырожденной, если определитель не равен нулю: . В противном случае ( ) матрицаА называется вырожденной.

Матрицей, союзнойк матрицеА, называется матрица

,

где - алгебраическое дополнение элемента данной матрицыА (оно определяется так же, как и алгебраическое дополнение элемента определителя).

Матрица называется обратной матрицеА, если выполняется условие:

, (3.1)

гдеЕ – единичная матрица того же порядка, что и матрица А. Матрица имеет те же размеры, что и матрица А.

Обратная матрица

Теорема 3.1.Всякая невырожденная матрица имеет обратную.

Приведем доказательство для случая матрицы 3-го порядка. Пусть

, причем .

Составим союзную матрицу

и найдем произведение матриц :

т.е.

(3.2)

Здесь мы использовали свойства 7 и 8 определителей (см. п. 2.2).

Аналогично убеждаемся, что

. (3.3)

Равенства (3.2) и (3.3) перепишем в виде

и

Сравнивая полученные результаты с определением (3.1), получим

т.е. .

Отметим свойства обратной матрицы:

1. ;

2. ;

3. .