Как решать задачу в случае кратных собственных чисел?

Общий алгоритм остаётся прежним, но здесь есть свои особенности, и некоторые участки решения целесообразно выдержать в более строгом академичном стиле:

Пример 6

Найти собственные числа и собственные векторы

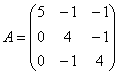
Решение: составим и решим характеристическое уравнение:

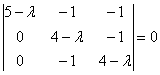
Конечно же, оприходуем сказочный первый столбец:

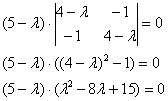
И, после разложения квадратного трёхчлена на множители:

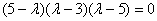
В результате получены собственные числа 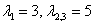, два из которых кратны.

Найдем собственные векторы:

1) С одиноким солдатом 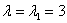разделаемся по «упрощённой» схеме:

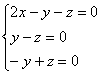
Из последних двух уравнений четко просматривается равенство 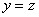, которое, очевидно, следует подставить в 1-е уравнение системы:

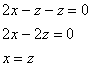
Лучшей комбинации не найти: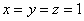
Собственный вектор: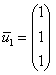

2-3) Теперь снимаем пару часовых. В данном случае может получиться либо два, либо один собственный вектор. Невзирая на кратность корней, подставим значение 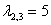в определитель 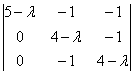, который приносит нам следующую однородную систему линейных уравнений:

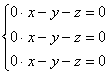
Собственные векторы – это в точности векторы
фундаментальной системы решений

Собственно, на протяжении всего урока мы только и занимались тем, что находили векторы фундаментальной системы. Просто до поры до времени данный термин особо не требовался. Кстати, те ловкие студенты, которые в маскхалатах проскочили тему однородных уравнений, будут вынуждены вкурить её сейчас.

Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

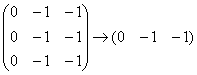
Единственное действие состояло в удалении лишних строк. В результате получена матрица «один на три» с формальной «ступенькой» посередине.
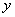– базисная переменная, 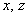– свободные переменные. Свободных переменных две, следовательно, векторов фундаментальной системы тоже два.

Выразим базисную переменную через свободные переменные: 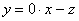. Нулевой множитель перед «иксом» позволяет принимать ему совершенно любые значения (что хорошо видно и из системы уравнений).

В контексте данной задачи общее решение удобнее записать не в строку, а в столбец:

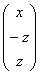
Паре 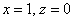соответствует собственный вектор: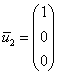
Паре 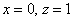соответствует собственный вектор: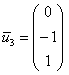

Примечание: искушенные читатели могут подобрать данные векторы и устно – просто анализируя систему 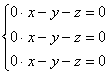, но тут нужны некоторые знания: переменных – три, ранг матрицы системы – единица, значит, фундаментальная система решений состоит из 3 – 1 = 2 векторов. Впрочем, найдённые векторы отлично просматриваются и без этих знаний чисто на интуитивном уровне. При этом даже «красивее» запишется третий вектор: 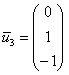. Однако предостерегаю, в другом примере простого подбора может и не оказаться, именно поэтому оговорка предназначена для опытных людей. Кроме того, а почему бы не взять в качестве третьего вектора, скажем, 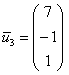? Ведь его координаты тоже удовлетворяют каждому уравнение системы, и векторы 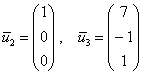линейно независимы. Такой вариант, в принципе, годен, но «кривоват», поскольку «другой» вектор 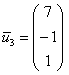представляет собой линейную комбинацию 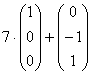векторов фундаментальной системы.

Ответ: собственные числа: 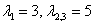, собственные векторы: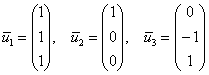

Аналогичный пример для самостоятельного решения:

Пример 7

Найти собственные числа и собственные векторы

Примерный образец чистового оформления в конце урока.

Следует отметить, что и в 6-м и в 7-м примере получается тройка линейно независимых векторов, поэтому исходная матрица представима в каноническом виде 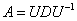. Но такая малина бывает далеко не во всех случаях:

Пример 8

Найти собственные числа и собственные векторы матрицы

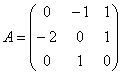
Решение: составим и решим характеристическое уравнение:

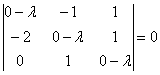
Определитель раскроем по первому столбцу:

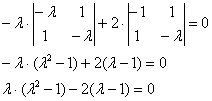
Дальнейшие упрощения проводим согласно рассмотренной методике, избегая многочлена 3-й степени:

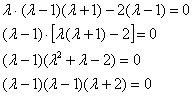
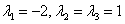– собственные значения.

Найдем собственные векторы:

1) С корнем 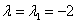затруднений не возникает:

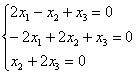
Не удивляйтесь, помимо комплекта 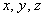в ходу также переменные 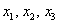– разницы тут никакой.

Из 3-го уравнения выразим 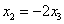– подставим в 1-е и 2-е уравнения:

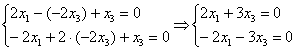
Из обоих уравнений следует: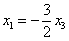

Пусть 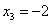, тогда:

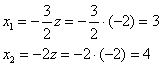
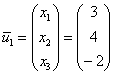
2-3) Для кратных значений 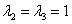получаем систему .

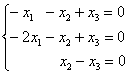Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

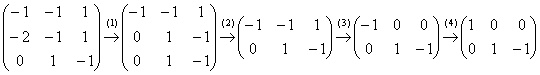
(1) Ко второй строке прибавили первую строку, умноженную на –2.

(2) Последние две строки одинаковы, одну из них удалили.

(3) Дальше пошла уместная доводка матрицы методом Гаусса-Жордана: к первой строке прибавили вторую строку.

(4) У первой строки сменили знак.

Переменные 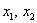– базисные, переменная 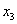– свободная. Так как свободная переменная одна, то фундаментальная система решений состоит из одного вектора. И мы счастливые наблюдатели случая, когда кратным собственным числам соответствует единственный собственный вектор. Записываем в столбец общее решение системы: 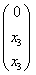, и, задавая свободной переменной значение 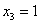, получаем нашего героя:

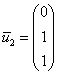
Ответ: собственные числа: 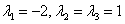, собственные векторы: .

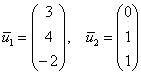Исходную матрицу нельзя представить в базисе из собственных векторов 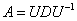по той простой причине, что такого базиса не существует – хоть трёхмерные векторы-столбцы и линейно независимы, но самих-то их всего лишь два. Недобор.

11.Квадратичные формы. Канонический вид.

Квадратичные формы.
Знакоопределённость форм. Критерий Сильвестра

Прилагательное «квадратичный» сразу наталкивает на мысль, что что-то здесь связано с квадратом (второй степенью), и очень скоро мы узнаем это «что-то» и что такое форма. Прямо скороговоркой получилась :)

Приветствую вас на своём новом уроке, и в качестве незамедлительной разминки мы рассмотрим форму в полосочку линейную. Линейной формой переменных называют однородный многочлен 1-й степени:

, где:

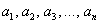– какие-то конкретные числа* (предполагаем, что хотя бы одно из них отлично от нуля), а – переменные, которые могут принимать произвольные значения.

* В рамках данной темы будем рассматривать только действительные числа.

С термином «однородный» мы уже сталкивались на уроке об однородных системах линейных уравнений, и в данном случае он подразумевает, что у многочлена нет приплюсованной константы .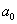

Например: – линейная форма двух переменных

Теперь форма квадратичная. Квадратичной формой переменных называют однородный многочлен 2-й степени, каждое слагаемое которого содержит либо квадрат переменной, либо парное произведение переменных. Так, например, квадратичная форма двух переменных 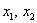имеет следующий вид:

Внимание! Это стандартная запись, и что-то менять в ней не нужно! Несмотря на «страшный» вид, тут всё просто – двойные подстрочные индексы констант сигнализируют о том, какие переменные входят в то или иное слагаемое:
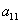– в этом слагаемом находится произведение и (квадрат);
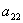– здесь произведение ;
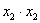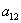– и здесь произведение .

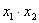Далее будем полагать, что хотя бы одна из констант не равна нулю, и вот, пожалуйста, «неполный» пример: 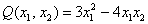, в котором:

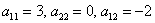– сразу упреждаю грубую ошибку, когда теряют «минус» у коэффициента, не понимая, что он относится к слагаемому: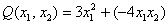

Иногда встречается «школьный» вариант оформления в духе 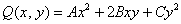, но то лишь иногда. Кстати, заметьте, что константы 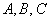нам тут вообще ни о чем не говорят, и поэтому запомнить «лёгкую запись» труднее. Особенно, когда переменных больше.

И квадратичная форма трёх переменных содержит уже шесть членов:

…почему в «смешанных» слагаемых ставятся множители-«двойки»? Это удобно, и скоро станет понятно, почему.

Далее ситуация начинает усугубляться:

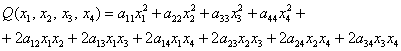
и усугублять мы её дальше не будем, т.к. формы с бОльшим количеством переменных встречаются довольно редко.

Однако общую формулу запишем, её удобно оформить «простынёй»:

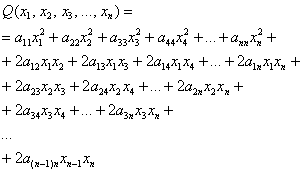
– внимательно изучаем каждую строчку – ничего страшного тут нет!

Квадратичная форма содержит слагаемых с квадратами переменных и 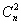слагаемых с их парными произведениями (см. комбинаторную формулу сочетаний). Больше ничего – никаких «одиноких иксов» и никакой приплюсованной константы (тогда уже получится не квадратичная форма, а неоднородный многочлен 2-й степени).