Определение эффективного множества с учетом безрискового кредитования

Марковиц в своей модели рассмотрел портфели ценных бумаг, состоящие только из рисковых активов. С появлением на рынке безрискового актива инвестор получил возможность вкладывать часть своих денег в этот актив, а остаток – в любой из рисковых активов. Инвестирование в безрисковый актив часто называют безрисковым кредитованием. Появление новых возможностей изменяет расположение значительной части эффективного множества Марковица.

Обозначим через 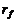безрисковую процентную ставку, через - математическое ожидание и среднеквадратическое отклонение доходности оптимального портфеля А.

Тогда ожидаемое значение и дисперсия доходности портфеля, составленного из доли безриского актива и доли ( ) портфеля А, будут соответственно

, (2.4.1)

.

Так как , то

. (2.4.2)

Из уравнений (2.4.1) и (2.4.2) получаем

,

. (2.4.3)

Из (2.4.3) видим, что все портфели, являющиеся комбинацией безрискового актива и рискового портфеля А, лежат на прямой.

Определим структуру эффективного множества в случае безрискового кредитования. Так как ожидания инвесторов однородны, каждый из них одинаково оценивает множество эффективных портфелей. Таким образом, каждый инвестор выберет один и тот же оптимальный портфель М, называемый рыночным портфелем. Этот оптимальный портфель можно найти из геометрических соображений, зная эффективное множество.

Сдвиг точки А вдоль эффективной границы вверх-вправо увеличивает эффективность объединённого портфеля, так как для тех же рисков доходность становится выше. Однако всему есть предел, когда прямая, соответствующая объединённому портфелю, касается эффективного множества в точке М (рис.2.4.1).

Рис. 2.4.1. Эффективное множество с возможностью безрискового кредитования

Выбираем оптимальное сочетание риска и доходности портфеля из безрискового актива и рыночного портфеля. Эффективное множество состоит из отрезка и участка кривой. Отрезок идет от безрискового актива в точку М и поэтому представляет портфели, составленные из различных комбинаций безрискового актива и портфеля М (рис.2.4.1). Участок кривой расположен выше и правее точки М и представляет портфели из эффективного множества модели Марковица.

Если инвестор склонен избегать высокий риск, то его портфель будет состоять из вложений части капитала в безрисковый актив и остальной части в портфель М. Если же инвестор готов рисковать с целью получения большего дохода, то его оптимальный портфель вообще не будет содержать безрискового актива.

Пример 2.4.1. Определить состав и характеристики портфеля, являющегося комбинацией безрискового актива с и первого «углового» портфеля эффективного множества из примера 2.3.1 в отношении 1:1.

Решение. Первый «угловой» портфель имеет вид

.

Новый портфель будет определяться так:

.

Математическое ожидание доходности и среднее квадратическое отклонение равны соответственно

,

.

Таким образом, новый портфель обладает ожидаемой доходностью равной 1,0715 и средним квадратическим отклонением 0,463.

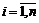Пусть портфель инвестора с капиталом, равным , составлен из ценных бумаг: рисковых - в количествах со стоимостями , , и безрискового актива с вложенной в него долей имеющегося капитала равной В. Тогда бюджетное ограничение при наличии вложения в безрисковый актив будет иметь вид

.

Разделив обе части этого уравнения на , получаем эквивалентное уравнение ,

где , , 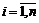- доли рисковых и безрисковых активов в портфеле.

Упражнения

1. Инвестор владеет рисковым портфелем, имеющим 20%-ную ожидаемую доходность. Безрисковая доходность равна 8%. Какова ожидаемая доходность нового портфеля, если инвестор вкладывает следующую долю своих средств в рисковый портфель, а остаток в безрисковый актив:

а) 90%;

б) 45%;

в) 60%.

2. Портфель, составленный из рисковых ценных бумаг, имеет ожидаемую доходность 24% и среднее квадратическое отклонение 15%. Если безрисковая процентная ставка 5%, то как можно составить портфель, имеющий ожидаемую доходность 19,25%? Каково среднее квадратическое отклонение этого портфеля?

3. Портфель состоит из инвестиций в рисковый портфель, дающий 15%-ную доходность и 20%-ное среднее квадратическое отклонение, и в безрисковый актив с доходностью 8%. Определить, чему равна ожидаемая доходность полученного портфеля, если среднее квадратическое отклонение его равно 12%.

4. Даны вектор ожидаемых доходностей и матрица ковариаций трех активов

М= , = .

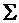а) Какой из трех активов является безрисковым? Почему?

б) Определить состав портфеля, если его ожидаемая доходность 10% и дисперсия 30,25.

5. На рынке существуют два вида акций с совместным законом распределения

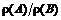	0,05	0,2	0,15
	0,3	0,2	0,1

Найти среднее значение и среднеквадратическое отклонение доходности всего портфеля Р, состоящего наполовину из акций вида А и наполовину из акций вида В. Определить доходность и среднеквадратическое отклонение доходности нового портфеля, если он на 30% состоит из безрисковых ценных бумаг со ставкой дохода % и на 70% из данного портфеля Р.