Случайные события. Алгебра случайных событий

Теория вероятностей имеет дело с математическими моделями опытов (экспериментов, наблюдений, испытаний) со случайными исходами (случайных опытов). Всякий случайный опыт состоит в осуществлении некоторого вполне определенного комплекса условий 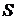и наблюдении результата. Рассматриваются только такие опыты, которые можно (хотя бы в принципе) воспроизводить при неизменном комплексе условий произвольное число раз.

В случайных опытах наблюдается неоднозначность результата при повторении опыта с сохранением основных условий его проведения. Предметом наблюдения в том или ином случайном опыте может быть некоторый процесс, физическое или социальное явление, действующая система. Для реально воспроизводимого опыта понятие «наблюдаемый результат» означает, что существует принципиальная возможность регистрации данного результата опыта. Любой наблюдаемый результат интерпретируется как случайный исход опыта (случайное событие). Событие может произойти, а может и не произойти в результате опыта.

Случайными событиями являются, например, выпадение «герба» при подбрасывании монеты, результаты измерений, процент брака на предприятии в тот или иной день недели и т. д.

При построении математической модели некоторого случайного опыта (вероятностной модели) исходным пунктом является построение множества элементарных исходов 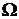, связанного с данным опытом. Это множество представляет собой множество всех возможных, взаимоисключающих исходов такое, что результатом опыта всегда является один и только один из этих возможных исходов. Любое подмножество множества 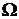интерпретируется как событие (возможно, и не наблюдаемое).

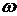Говорят, что событие наступило (произошло, осуществилось, реализовалось), если результатом опыта явился элементарный исход , принадлежащий ( ).

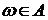Множество 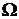может быть дискретным или непрерывным. К первым относятся конечные или счетные множества элементарных исходов, ко вторым – множества типа континуума (любой конечный или бесконечный интервал на числовой оси является примером множества типа континуума).

Построение множества 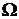(если оно не задано при описании опыта) осуществляется на практике, исходя из требования, чтобы все интересующие нас результаты данного опыта могли быть однозначно описаны на основе построенного множества 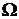. Другими словами, если нас интересуют события , , 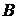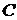и т. д., являющиеся наблюдаемыми событиями в данном опыте, то множество 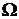должно состоять из таких исходов, чтобы существовали подмножества данного множества, равносильные событиям , , 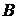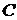и т. д. В совокупности всех подмножеств множества 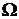, соответствующих совокупности всех наблюдаемых событий для данного опыта (поле событий), элементарные исходы будут одноэлементными подмножествами.

Пример. Подбрасывается один раз правильная шестигранная игральная кость. Обозначим через 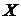число очков, выпавших на верхней грани кости. Построить множество элементарных исходов и описать состав подмножеств, соответствующих следующим событиям: , , , .

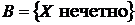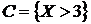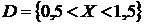◄ Обозначим через 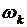события, состоящие в выпадении 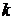очков: 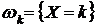, 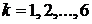. Эти события и будут элементарными исходами в данном опыте, т. к. все интересующие нас события могут быть описаны как подмножества множества элементарных исходов 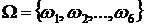. Действительно, 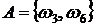, , 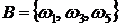, 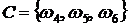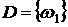. Отметим, что событие, совпадающее со всем множеством 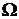всегда происходит (обязательно выпадет то или иное число очков 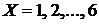). Другими словами, событие 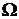есть достоверное событие (см. ниже). ►

Пример. Монета подбрасывается три раза. Наблюдаемый результат – появление герба или решки на верхней стороне монеты. Построить множество 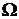и подмножества, соответствующие событиям: , , .

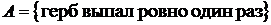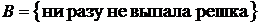◄ Обозначим выпадение герба символом «Г», а решки – «Р». Так, запись РГР будет обозначать результат опыта, в котором при первом и третьем подбрасывании выпала решка, а при втором – герб. Множество элементарных исходов состоит из восьми исходов: 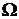={ГГГ, ГГР, ГРГ, РГГ, ГРР, РГР, РРГ, РРР}. События ={ГРР, РГР, РРГ}, 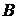={ГГГ}, 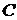={ГГР, РГГ, ГГГ}. ►

Поскольку события отождествляются с множествами, то над ними можно совершать все операции, выполняемые над множествами.

Событие, совпадающее с пустым множеством 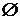, называется невозможным событием (при создании комплекса условий 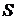, характеризующих опыт, оно никогда не наступит).

Событие, совпадающее со всем множеством 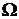, называется достоверным событием (оно всегда происходит при создании комплекса условий ).

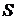Два события и 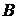называются совместными(несовместными), если в результате опыта возможно (невозможно) их совместное осуществление. Другими словами, события и совместны, если соответствующие множества и 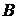имеют общие элементы, и несовместны в противном случае.

Между событиями определяются следующие операции и отношения:

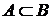– событие влечет за собой событие 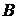(отношение включения множеств: множество является подмножеством множества 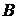). Иначе говоря, событие 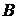происходит всякий раз, как происходит событие .

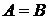– событие тождественно событию 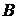(отношение эквивалентности множеств). Это возможно в том и только том случае, когда 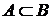и .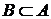

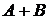– сумма событий (объединение множеств). Это событие, состоящее в том, что произошло хотя бы одно из двух событий или 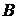(неисключающее логическое «или»).

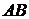– произведение событий(пересечение множеств). Это событие, состоящее в совместном осуществлении событий и 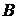(логическое «или»). Таким образом, события и 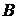несовместны, если .

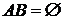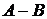– разность событий (множество элементов, принадлежащих , но не принадлежащих 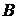). Это событие, состоящее в том, что происходит, а 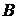не происходит.

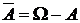– противоположное событие (дополнение множества до 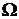). Это событие, состоящее в том, что не происходит (логическое отрицание).

Сумму событий 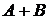часто обозначают символом 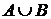, а произведение – .

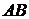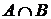Полная группа несовместных событий. Система 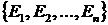называется разбиениеммножества 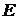, если выполняются следующие условия:

,

,

.

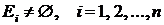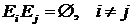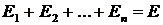Если разбиению подвергается множество элементарных исходов 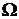некоторого опыта, то говорят, что система подмножеств (событий), осуществляющих разбиение, составляет полную группу несовместных событий.

Полезной является геометрическая иллюстрация событий, при которой они трактуются как попадание точки в область, соответствующую этому событию. Условно изображая события в виде различных областей на плоскости, получаем так называемые диаграммы Венна. На рис. 1 приведена такая геометрическая иллюстрация некоторых отношений и операций над событиями, определенных выше.

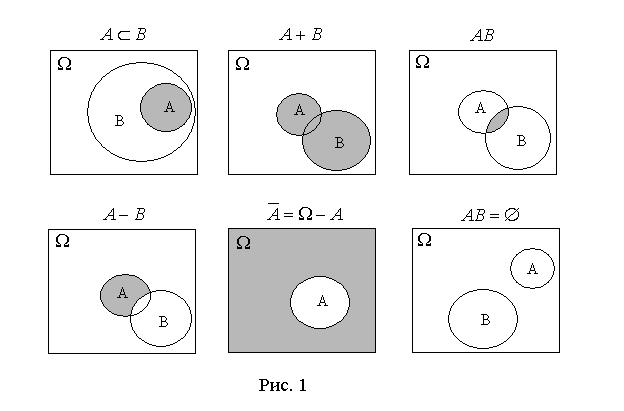
Бинарные операции сложения и умножения событий обладают следующими свойствами:

1) 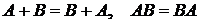(коммутативные законы);

2) 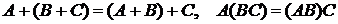(ассоциативные законы);

3) 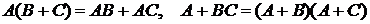(дистрибутивные законы);

4) 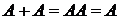(свойства идемпотентности);

5) 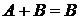в том и только в том случае, если 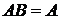(свойство совместимости). Кроме того,

6) ;

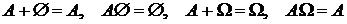7) ;

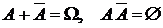8) 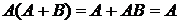(законы поглощения);

9) 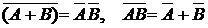(двойственность, законы де Моргана);

10) .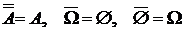