Тема 22 Итерационные методы решения систем линейных алгебраических уравнений

Лекция 22.1 «Итерационные методы решения систем линейных алгебраических уравнений»

Учебные вопросы:

1. Метод простых итераций для решения систем линейных алгебраических уравнений

2. Метод Зейделя

3. Метод релаксации

Пусть дана система линейных алгебраических уравнений (СЛАУ) вида

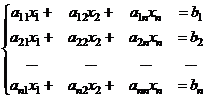(4.1)

Вводя в рассмотрение матрицы

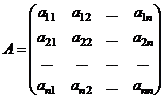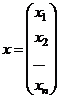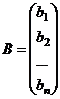, , (4.2)

систему (4.1) можно записать в виде матричного уравнения

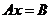. (4.3)

Для решения систем линейных алгебраических уравнений существуют точные методы: метод Гаусса, с помощью обратной матрицы (матричный метод), по формулам Крамера. Однако, при большом числе неизвестных применение точных методов решения затруднено. В этом случае для нахождения корней системы (4.1) целесообразнее пользоваться приближенными (численными) методами, которые и будут рассмотрены в данной лекции.

Пусть дана система линейных алгебраических уравнений вида (4.1).

Предположим, что диагональные элементы матрицы 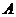не равны нулю, т.е. 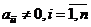(в случае равенства одного или нескольких из них нулю, с помощью перестановки уравнений или других эквивалентных преобразований можно добиться, чтобы они были отличны от нуля). Разделив 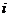-ое уравнение системы на 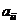, получим:

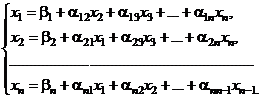(4.4)

где коэффициенты 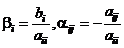при .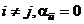

Введем обозначения:

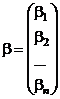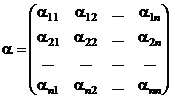, (4.5)

Тогда система (4.4) примет вид:

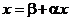(4.6)

Систему (4.6) будем решать методом последовательных приближений. Выбираем начальное приближение 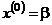; далее вычисляем следующие приближения:

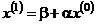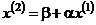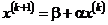, ,…, , … (4.7)

Если последовательность приближений 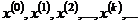является сходящейся, т.е. у нее существует предел 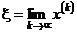, то этот предел 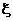является решением системы (4.6). Действительно,

.

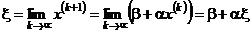Получили 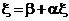, т.е. 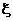– является решением системы (4.6), а система (4.6) получена из системы (4.1), следовательно, 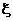будет являться решением исходной системы (4.1).

Теорема 4.1(достаточное условие сходимости итерационного процесса).

Если для приведенной системы 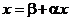выполнено хотя бы одно из условий:

а)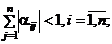

б) ,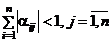

то процесс итерации, заданный формулой 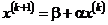, сходится к единственному решению этой системы, независимо от выбора начального приближения.

В частности процесс итерации заведомо сходится, если элементы 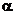приведенной системы (4.4) удовлетворяют неравенству 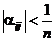, где 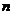- число неизвестных системы.

Следствие

Для исходной системы (4.1) итерационный процесс сходится, если выполнены неравенства 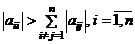(то есть модули диагональных коэффициентов для каждого уравнения системы больше суммы модулей всех остальных коэффициентов, не считая свободных членов).

Теорема 4.2 (необходимое и достаточное условие сходимости процесса итерации для системы линейных уравнений).

Для сходимости процесса итераций: 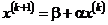при любом выборе начального приближения 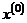и любом свободном члене 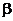необходимо и достаточно, чтобы собственные значения матрицы 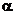(т.е. корни характеристического уравнения 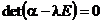) были по модулю меньше единицы.