Алгоритм нахождения максимального пути

При решении некоторых практических задач возникает необходимость поиска максимального пути (пути с наибольшей суммой длин дуг). Такая задача сводится к задаче нахождения минимального пути заменой знаков при длинах дуг (в матрице весов C) на противоположные. При этом необходимым является требование отсутствия в ориентированном графе контуров положительной длины.

Пример 3.16.

С помощью модифицированного алгоритма 3.1 найдем максимальный путь из верши­ны х₁ в вершину х₃ в графе, изображенном на рис. 3.11.

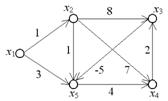
Рис. 3.11

Шаг 1. Введем число вершин графа n =5. Матрица весов этого графа после замены знаков при длинах дуг на противоположные имеет вид:

C = .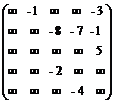

Шаг 2. Положим k = 0, l₁(0) = 0, l₂(0) = l₃(0) = l₄(0) = l₅(0) = 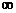. Эти значения занесем в первый столбец табл. 3.2.

Шаг 3.

k = 1.

l₁(1) = 0.

Равенство (3.1) для k = 1 имеет вид:

l_i(1) = 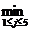{l_j(0) + c_ji}.

l₂(1) = min{l₁(0) + c₁₂; l₂(0) + c₂₂; l₃(0) + c₃₂; l₄(0) + c₄₂; l₅(0) + c₅₂;} = min{0 – 1; ¥ + ¥; ¥ + ¥; ¥ + ¥; ¥ + ¥} = –1.

l₃(1) = min{l₁(0) + c₁₃; l₂(0) + c₂₃; l₃(0) + c₃₃; l₄(0) + c₄₃; l₅(0) + c₅₃;} = min{0 + ¥ ; ¥ – 8; ¥ + ¥; ¥ – 2; ¥ + ¥} = ¥ .

l₄(1) = min{l₁(0) + c₁₄; l₂(0) + c₂₄; l₃(0) + c₃₄; l₄(0) + c₄₄; l₅(0) + c₅₄;} = min{0 + ¥ ; ¥ – 7; ¥ + ¥; ¥ + ¥; ¥ – 4} = ¥ .

l₅(1) = min{l₁(0) + c₁₅; l₂(0) + c₂₅; l₃(0) + c₃₅; l₄(0) + c₄₅; l₅(0) + c₅₅;} = min{0 – 3; ¥ – 1; ¥ + 5; ¥ + ¥; ¥ + ¥} = –3.

Полученные значения l_i(1) занесем во второй столбец табл. 3.2. Убеждаемся, что второй столбец, начиная со второго элемента, совпадает с первой строкой матрицы весов, что легко объясняется смыслом величин l_i(1), которые равны длине минимального пути из первой вершины в i-ую, содержащего не более одной дуги.

k = 2.

l₁(2) = 0.

Равенство (3.1) для k = 2 имеет вид:

l_i(2) = 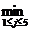{l_j(1) + c_ji}.

l₂(2) = min{0 – 1; –1 + ¥; ¥ + ¥; ¥ + ¥; –3 + ¥} = –1.

l₃(2) = min{0 + ¥ ; –1 – 8; ¥ + ¥; ¥ – 2; –3 + ¥} = –9 .

l₄(2) = min{0 + ¥ ; –1 – 7; ¥ + ¥; ¥ + ¥; –3 – 4} = –8 .

l₅(2) = min{0 – 3; –1 – 1; ¥ + 5; ¥ + ¥; –3 + ¥} = –3.

Полученные значения l_i(2) занесем в третий столбец табл. 3.2. Величины l_i(2) равны длине минимального пути из первой вершины в i-ую, содержащего не более двух дуг.

k = 3.

l₁(3) = 0.

Равенство (3.1) для k = 3 имеет вид:

l_i(3) = 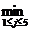{l_j(2) + c_ji}.

l₂(3) = min{0 – 1; – 1 + ¥; – 9 + ¥; –8 + ¥; – 3 + ¥} = – 1.

l₃(3) = min{0 + ¥ ; – 1 – 8; – 9 + ¥; –8 – 2; – 3 + ¥} = – 10 .

l₄(3) = min{0 + ¥ ; – 1 – 7; – 9 + ¥; –8 + ¥; – 3 – 4} = – 8 .

l₅(3) = min{0 – 3; – 1 – 1; – 9 + 5; –8 + ¥; – 3 + ¥} = – 4.

Полученные значения l_i(3) занесем в четвертый столбец табл. 3.2. Величины l_i(3) равны длине минимального пути из первой вершины в i-ую, содержащего не более трех дуг.

k = 4.

l₁(4) = 0.

Равенство (3.1) для k = 4 имеет вид:

l_i(4) = 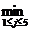{l_j(3) + c_ji}.

l₂(4) = min{0 – 1; – 1 + ¥ ; – 10 + ¥; – 8 + ¥; – 4 + ¥} = – 1.

l₃(4) = min{0 + ¥ ; – 1 – 8; – 10 + ¥; – 8 – 2; – 4 + ¥} = – 10 .

l₄(4) = min{0 + ¥ ; – 1 – 7; – 10 + ¥; – 8 + ¥; – 4 – 4} = – 8 .

l₅(4) = min{0 – 3; – 1 – 1; – 10 + 5; – 8 + ¥; – 4 + ¥} = – 5.

Полученные значения l_i(4) занесем в пятый столбец табл. 3.2. Величины l_i(4) равны длине минимального пути из первой вершины в i-ую, содержащего не более четырех дуг.

Таблица 3.2

i(номер вершины)	li(0) li(1) li(2) li(3) li(4)
	0 0 0 0 0 ¥ – 1 – 1 – 1 1 ¥ ¥ – 9 – 10 – 10 ¥ ¥ – 8 – 8 – 8 ¥ – 3 –3 – 4 – 5

Заменив в табл. 3.2 отрицательные числа положительными, получим таблицу индексов максимальных путей (табл. 3.3). При этом l_i(k) определяет длину максимального пути из первой вершины в i-ую, содержащего не более k дуг.

Таблица 3.3

i(номер вершины)	li(0) li(1) li(2) li(3) li(4)
	0 0 0 0 0 ¥ 1 1 1 1 ¥ ¥ 9 10 10 ¥ ¥ 8 8 8 ¥ 3 3 4 5

Шаг 5. Восстановление максимального пути производится по тому же правилу, что и для минимального пути.

Длина максимального пути равна 10. Этот путь состоит из трех дуг, т. к. l_i(3) = l_i(4) = 10. Поэтому в соотношении (3.2) будет выполнено, начиная с n – 1.

Учитывая это замечание, для последней вершины x₃предшествующую ей вершину x_r определим из соотношения (3.2) полученного при s =3:

l_r(2) + c_r3 = l₃(3), (3.7)

x_rÎ G^-1(x₃), где G^-1(x₃) - прообраз вершины x₃.

G^-1(x₃)= {x₂, x₄}.

Подставим в (3.7) последовательно r = 2 и r = 4, чтобы определить, для какого r это равенство выполняется:

l₂(2) + c₂₃ = 1 + 8 ¹ l₃(4) = 10,

l₄(2) + c₄₃ = 8 + 2 = l₃(4) = 10.

Таким образом, вершиной, предшествующей вершине x₃, является вершина x₄.

Для вершины x₄предшествующая ей вершина x_r определяется из соотношения (3.2) полученного при s =4:

l_r(1) + c_r4 = l₄(2), x_rÎ G^-1(x₄), (3.8)

где G^-1(x₄) - прообраз вершины x₄.

G^-1(x₄)= {x₂, x₅}.

Подставим в (3.8) последовательно r = 2, r = 3 и r = 5, чтобы определить, для какого r это равенство выполняется:

l₂(1) + c₂₄ = 1 + 7 = l₄(3) = 8,

l₅(1) + c₅₄ = 3 + 4 ¹ l₄(3) = 8,

Таким образом, вершиной, предшествующей вершине x₄, является вершина x₂.

Для вершины x₂предшествующая ей вершина x_r определяется из соотношения (3.2) полученного при s =2:

l_r(0) + c_r2 = l₂(1), x_r 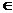G^-1(x₂), (3.9)

где G^-1(x₂) - прообраз вершины x₂.

G^-1(x₂)= {x₁}.

Подставим в (3.9) r = 1, чтобы определить, выполняется ли это равенство:

l₁(1) + c₁₂ = 0 + 1 = l₂(1) = 1.

Таким образом, вершиной, предшествующей вершине x₂, является вершина x₁.

Итак, найден максимальный путь – x₁, x₂, x₄, x₃, его длина равна 10.

Деревья

Основные определения

Неориентированным деревом(или просто деревом) называется связный граф без циклов. Этому определению эквивалентны, как легко показать, следующие определения:

а) дерево есть связный граф, содержащий n вершин и n - 1 ребер;

б) дерево есть граф, любые две вершины которого можно соединить простой цепью.

Пример 3.17.

Графы, изображенные на рис. 3.12, являются деревьями.

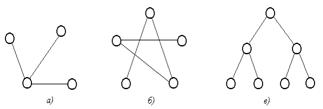
Рис. 3.12

Если граф несвязный и не имеет циклов, то каждая его связная компонента будет деревом. Такой граф называется лесом. Можно интерпретировать рис. 6.1 как лес, состоящий из трех деревьев.

Остовным деревомсвязного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом.

Пример 3.18.

Для графа, изображенного на рис. 3.13а), графы на рис. 3.13б) и 3.13в) являются остовными деревьями.

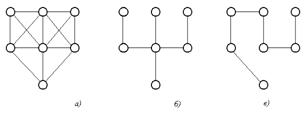
Рис. 3.13

Пусть граф G имеет n вершин и m ребер Так как всякое дерево с n вершинами по определению (см. раздел 6.1) имеет n – 1 ребер, то любое остовное дерево графа G получается из этого графа в результате удаления m –(n – 1) = m – n + 1 ребер. Число g = m – n + 1 называется цикломатическим числомграфа.