Теория регулярных линий передачи

На практике наибольшее распространениеполучили отрезки регуляр­ных линий передачи той или иной длины.Если длина регулярной линии передачи существенно превышает длину волны в линии λ_л, то такая линия называется длинной. Характерной особенностью длинных линий является возможность существования в них двух волн, распространяю­щихся навстречу друг другу. Одна из этих волн образуется подключен­ным к линии генератором электромагнитных колебаний и называется падающей. Другая волна образуется из-за отражения падающей волны от нагрузки, подключенной к противоположному концу линии, и называется отраженной. Отраженная волна распространяется в направлении, обратном падающей волне. Все разнообразие процессов, происходящих в длинной линии, определяется амплитудно-фазовыми соотношениями между падающей и отраженной волнами.

Рассмотрим двухпроводную длинную линию, представлен­ную на рис. 1, где Z_H = R_H + iX_H — комплексное сопротивление на­грузки; z — продольная координата линии, отсчитываемая от места подключения нагрузки.

Рис. 1. Двухпроводная длинная линия	Рис. 2. Эквивалентная схема участка длинной линии dz

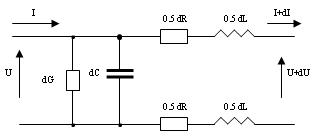
Из электродинамики известно, что линия передачи может быть охарактеризована ее погонными параметрами: R₁ — погонное сопро­тивление, Ом/м; G₁ — погонная проводимость, 1/Ом ·м; L₁—погон­ная индуктивность, Гн/м; С₁ — погонная емкость, Ф/м. Погонные со­противление R₁ и проводимость G₁ зависят от проводимости материала проводов и качества диэлектрика, окружающего эти провода, соответ­ственно. Чем меньше тепловые потери в металле проводов и в диэлек­трике, тем меньше, соответственно, R₁, и G₁. Погонные индуктивность L₁ и емкость С₁ определяются формой и размерами поперечного сече­ния проводов, а также расстоянием между ними. Выделим из линии элементарный участок бесконечно малой длины dz и рассмотрим его эквивалентную схему (рис. 2).

Значение параметров схемы можно определить из отношений

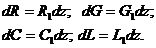(4)

На основе эквивалентной схемы запишем выражения для приращений тока и напряжения

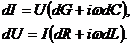(5)

Подставив в (5) значения параметров схемы из (4), получим

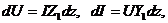
где 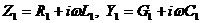– погонные комплексные сопротивление и проводимость линии. В этом случае

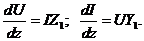(6)

Выражения (6) получили название телеграфных уравнений длинной линии, и именно они определяют связь между током и напряжением в любом сечении линии.

Решить телеграфные уравнения можно относительно напряжения и тока, если продифференцировать их по z:

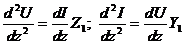. (7)

Также следует учесть, что

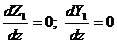. (8)

Полученные выражения являются математическим определением регулярности длинной линии. Физический смысл (8) в том, что погонные параметры не изменяются вдоль линии.

Подставив в (7) значения производных напряжения и тока из (6) и произведя ряд преобразований, получим

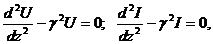(9)

где γ – коэффициент распространения волны в линии, (1/м).

Выражения (9) называются однородными волновыми уравнениями длинной линии. Их решения хорошо известны и могут быть записаны в виде [3]

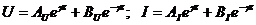, (10)

где A_U, B_U, A_I, B_I – некоторые коэффициенты, физический смысл которых будет пояснен позже, они имеют размерность напряжения и тока соответственно.

Решение волновых уравнений в виде (10) имеют характерный вид: первое слагаемое – это падающая волна напряжения или тока, которая распространяется от генератора к нагрузке; второе слагаемое – отраженная волна, которая распространяется от нагрузки к генератору. Таким образом, коэффициенты A_U, A_I представляют собой комплексные амплитуды падающих волн напряжения и тока соответственно, а коэффициенты B_U и B_I – комплексные амплитуды отраженных волн напряжения и тока. В связи с тем что часть мощности, которая передается по линии, может поглотиться в нагрузке, амплитуды отраженных волн не должны превышать амплитуды падающих:

.

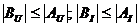В (10) направление распространения волны определяется знаком в показатели степени экспоненты: «плюс» – волна распространяется в отрицательном направлении оси z, «минус» – в положительном. В этом случае можно записать

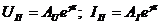. (11)

Коэффициент распространения γ в общем случае является комплексной величиной и представляется в виде

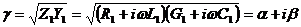, (12)

где α, 1/м – коэффициент затухания волны в линии; β, 1/м – коэффициент фазы.

Тогда, учитывая (12), выражения (11) примут вид

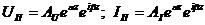. (13)

Коэффициент затухания α определяет скорость уменьшения амплитуды волны при распространении вдоль линии. Коэффициент фазы β определяет скорость изменения фазы волны вдоль линии.

Коэффициент β связан с длиной волны λ отношением

. (14)

Фазовая скорость волны в линии V_ф определяется через коэффициент фазы:

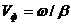. (15)

Определить решение однородных волновых уравнений можно и через значения напряжений и токов линии в нагрузке. В этом случае вводится понятие волнового сопротивления линии: 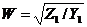(Ом). Тогда волновым сопротивлением линии передачи называется отношение напряжения к току в бегущей волне.

В этом случае выражения (10) примут вид

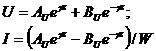(16)

Для нахождения коэффициентов А и В используем условие на конце линии z=0: U(z=0)=U_H; I(z=0)=I_H. Тогда из (16) при z=0 получим:

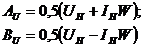(17)

Подставим полученные значения коэффициентов из (17) в (16) и после преобразований получим

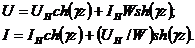(18)

где ch и sh – гиперболические синус и косинус.

С учетом проведенного решения телеграфных уравнений оценим закономерности изменения напряжения и тока вдоль линии передачи.

Сначала рассмотрим простейший случай, когда напряжение и ток в линии определяются только падающей волной, а отраженная волна отсутствует. Тогда B_U=0, B_I =0 и из (10) получим: .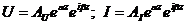

Рис. 3. Эпюры напряжения падающей волны в линии:

а – амплитуда, б – фаза

На рис. 3 представ­лены эпюры изменения ам­плитуды напряженияи фазына­пряжения вдоль линии. Эпю­ры изменения амплитуды и фазы тока имеют такой же вид. Из рассмотрения эпюр следует, что при отсутствии в линии потерь (α = 0) ампли­туда напряжения в любом се­чении линии остается одной и той же. При наличии потерь в линии (α > 0) часть перено­симой мощности преобразует­ся в тепло (нагревание прово­дов линии и окружающего их диэлектрика). По этой причи­не амплитуда напряжения па­дающей волны экспоненци­ально убывает в направлении распространения.

Фаза напряжения падающей волны изменяется по ли­нейному закону и уменьшается по мере удаления от генератора.

Рассмотрим изменение амплитуды и фазы, например, напряже­ния при наличии падающей и отраженной волн. Для упрощения поло­жим, что потери в линии отсутствуют, т.е. α= 0. Тогда напряжение в линии можно представить в виде

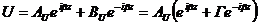, (19)

где Г = В_и / А_и — комплексный коэффициент отражения по напряже­нию. Он характеризует степень согласования линии передачи с нагруз­кой. Модуль коэффициента отражения изменяется в пределах: 0≤|Г|≤1. При этом |Г| = 0, если отражения от нагрузки отсутствуют и В_и = 0; |Г| = 1, если волна полностью отражается от нагрузки, т.е. .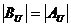

Соотношение (19) представляет собой сумму падающей и отраженной волн. Отобразим напря­жение на комплексной плоскости в виде вектор­ной диаграммы, каждый из векторов которой опре­деляет падающую, отра­женную волны и резуль­тирующее напряжение. Из диаграммы видно (рис. 4), что имеются такие поперечные сечения линии, где падающая и отраженная волны складываются в фазе. Напряжение в этих сечениях достигает максиму­ма, величина которого равна сумме амплитуд падающей и отраженной волн: 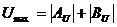. Кроме того, существуют такие поперечные се­чения линии, где падающая и отраженная волны складываются в противофазе. При этом напряжение достигает минимума.

Рис. 4. Векторная диаграмма напряжений в линии с отраженной волной

Если линия нагружена на сопротивление, для которого |Г| = 1, т.е. амплитуда падающей и отраженной волн равны, то в этом случае 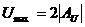, a U_min = 0. Напряжение в такой линии изменяется от нуля до удвоенной амплитуды падающей волны. По этому напряжению судят о степени согласования линии с на­грузкой. Для этого вводятся понятия коэффициента бегущей волны k_бв (КБВ) и коэффициента стоячей волны k_св (КСВ):

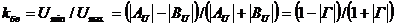; (20)

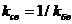. (21)

Эти коэффициенты изменяются в пределах:

.

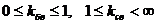На практике более часто используют понятие КСВ, т.к. современные измерительные приборы на индикаторных устройствах отображают измерение именно этой величины в определенной полосе частот.

Важной характеристикой линии передачи (длинной линии) является входное сопротивление 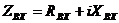, которое определяется в каждом сечении линии как отношение комплексных амплитуд напряжения и тока в этом сечении:

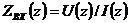. (22)

Входное сопротивление в общем случае носит комплексный характер и является частотно-зависимым. Кроме того, входное сопротивление зависит от длины отрезка линии и сопротивления нагрузки.

Режимы работы:

- согласования с нагрузкой (режим бегущей волны);

- смешанных волн (обычно имеющий место на практике);

- стоячей волны (в случае короткого замыкания, холостого хода, работы на чисто реактивную нагрузку).

В режиме стоячей волны при КЗ, ХХ, и L,C нагрузок в линии устанавливается стоячая волна напряжения (и тока), перенос энергии в продольном направлении невозможен.